Deduction 4 - What is the shape of a quadrilateral with all angles equal to 90°?

Transcript

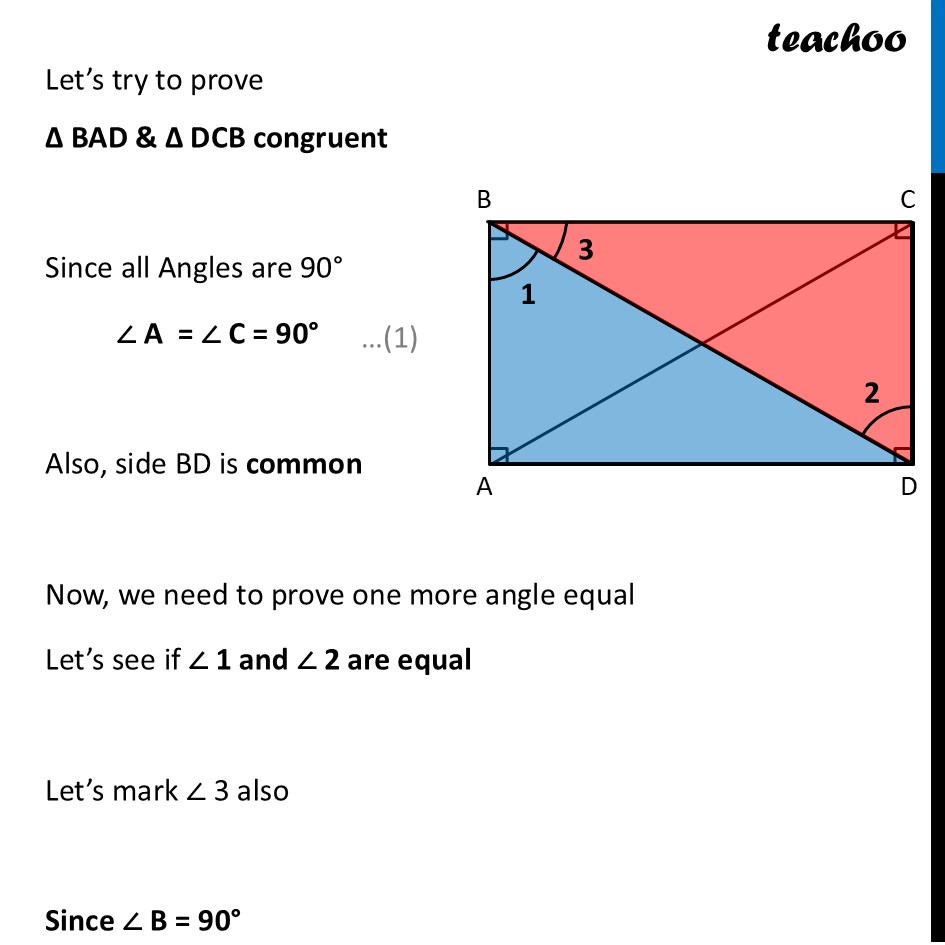
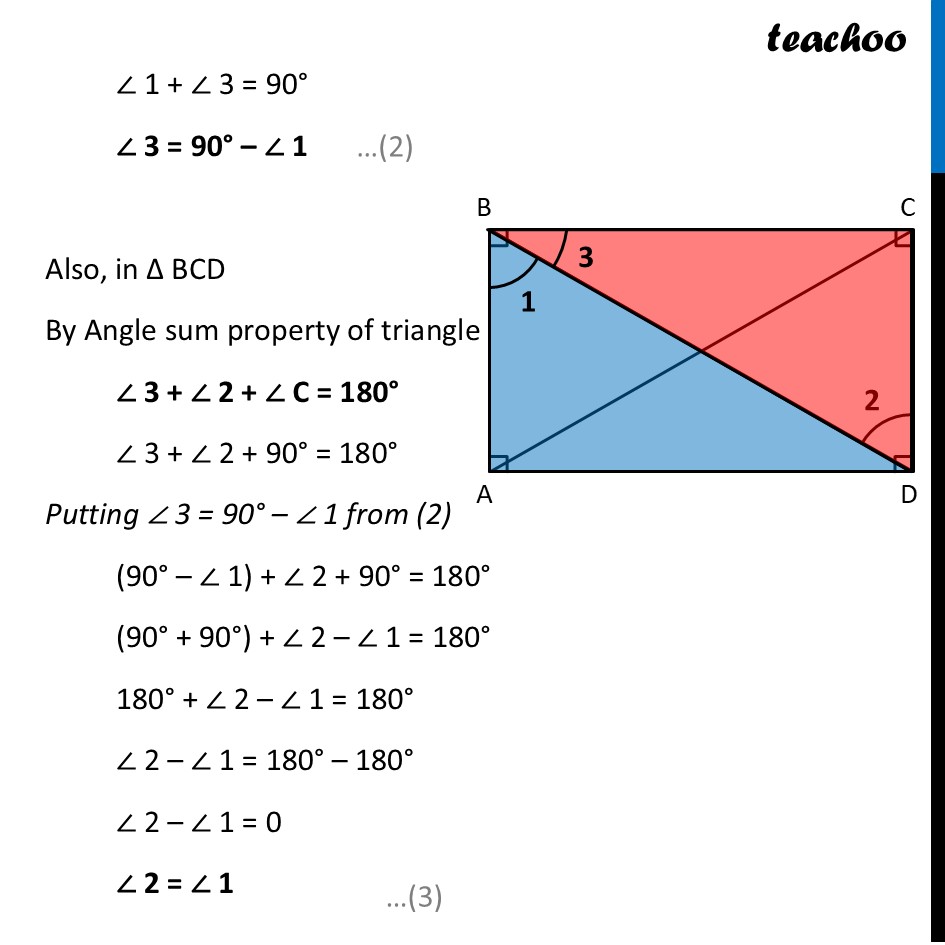
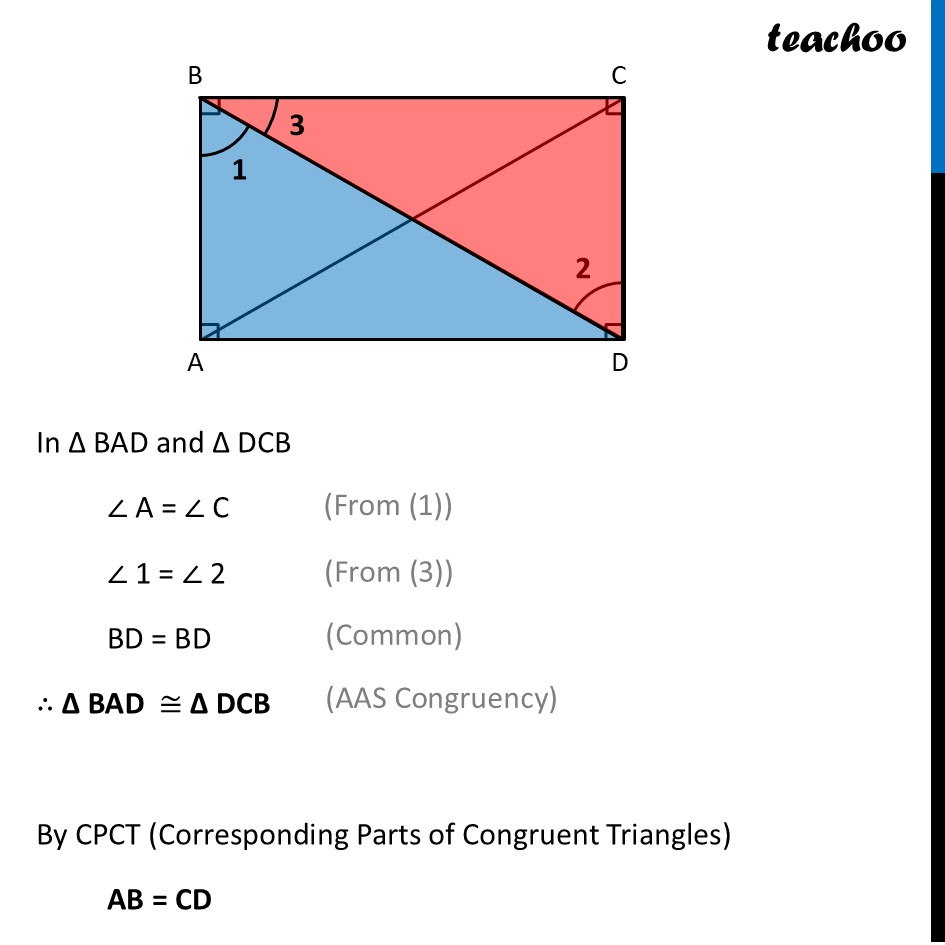
Deduction 4 What is the shape of a quadrilateral with all angles equal to 90°?Consider a quadrilateral ABCD with all angles measuring 90°. We try to check if any side is equal To do that, we try to check if any triangles are congruent Let’s try to prove ∆ BAD & ∆ DCB congruent Since all Angles are 90° ∠ A = ∠ C = 90° Also, side BD is common Now, we need to prove one more angle equal Let’s see if ∠ 1 and ∠ 2 are equal Let’s mark ∠ 3 also Since ∠ B = 90° ∠ 1 + ∠ 3 = 90° ∠ 3 = 90° – ∠ 1 Also, in ∆ BCD By Angle sum property of triangle ∠ 3 + ∠ 2 + ∠ C = 180° ∠ 3 + ∠ 2 + 90° = 180° Putting ∠ 3 = 90° – ∠ 1 from (2) (90° – ∠ 1) + ∠ 2 + 90° = 180° (90° + 90°) + ∠ 2 – ∠ 1 = 180° 180° + ∠ 2 – ∠ 1 = 180° ∠ 2 – ∠ 1 = 180° – 180° ∠ 2 – ∠ 1 = 0 ∠ 2 = ∠ 1 In ∆ BAD and ∆ DCB ∠ A = ∠ C ∠ 1 = ∠ 2 BD = BD ∴ ∆ BAD ≅ ∆ DCB By CPCT (Corresponding Parts of Congruent Triangles) AB = CD Similarly, we can prove AD = BC Thus, in ABCD, Both pairs of Opposite side is equal And all angles are 90° Therefore, ABCD is a rectangle