Deduction 3 - What are the angles between the diagonals?

Transcript

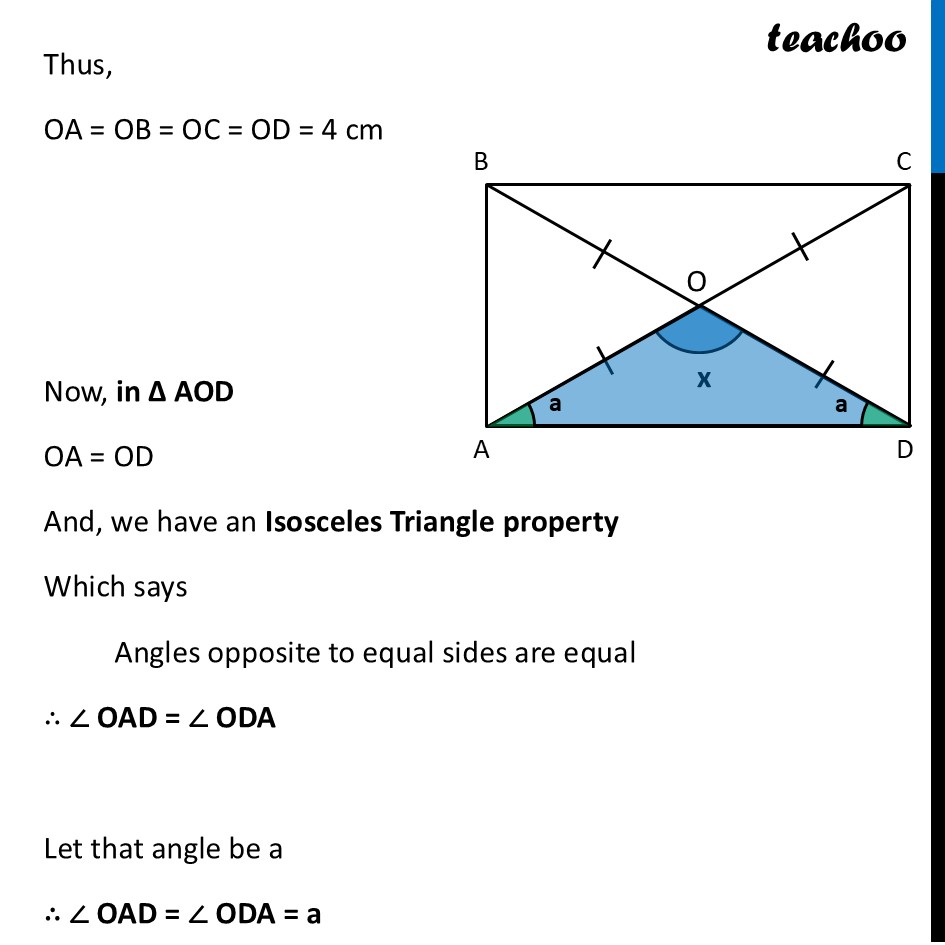
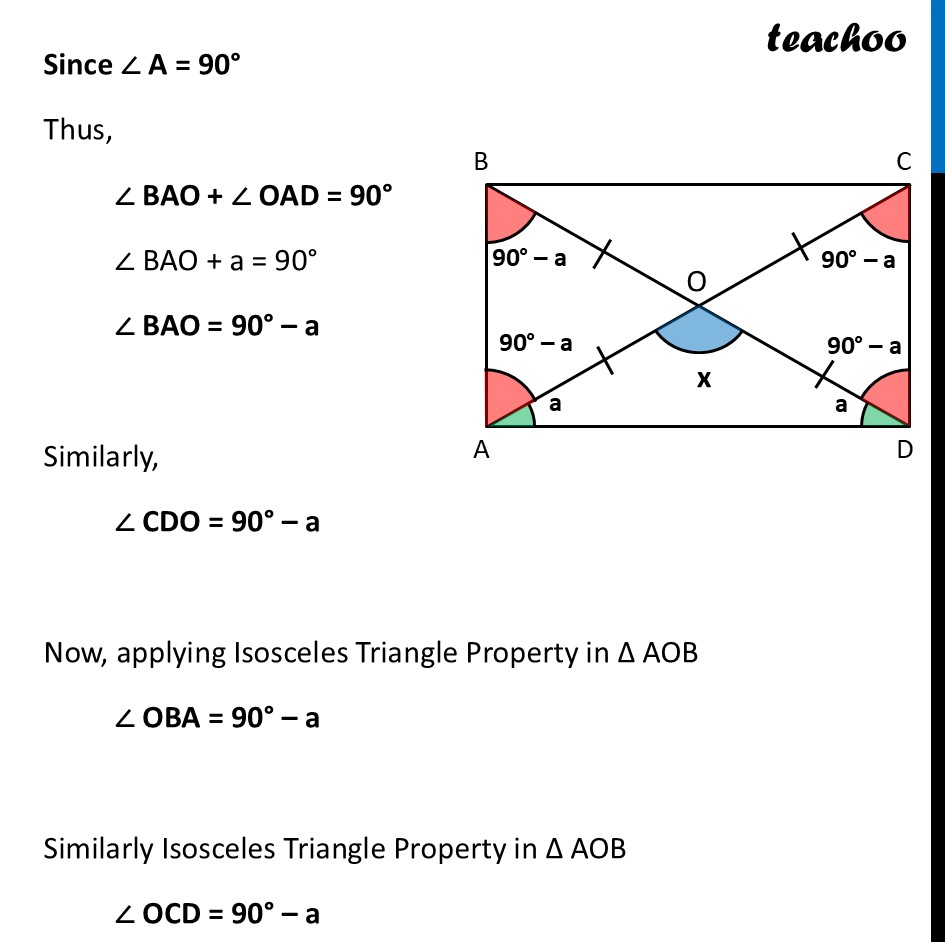
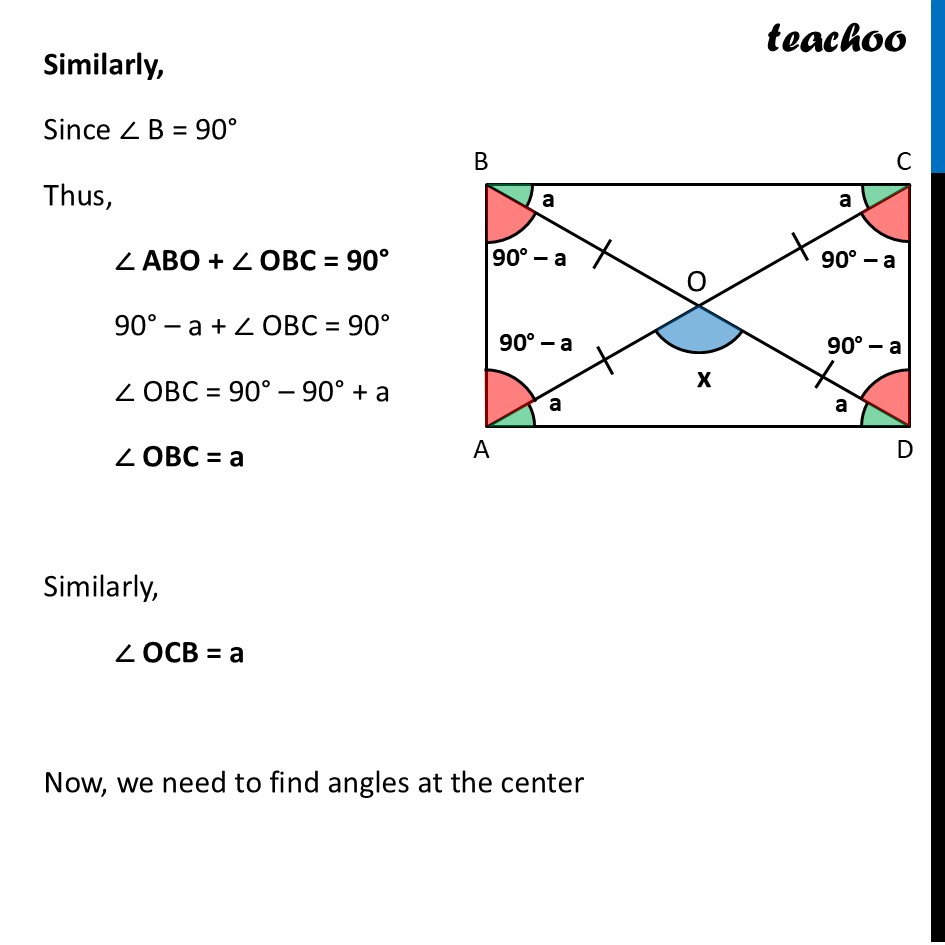
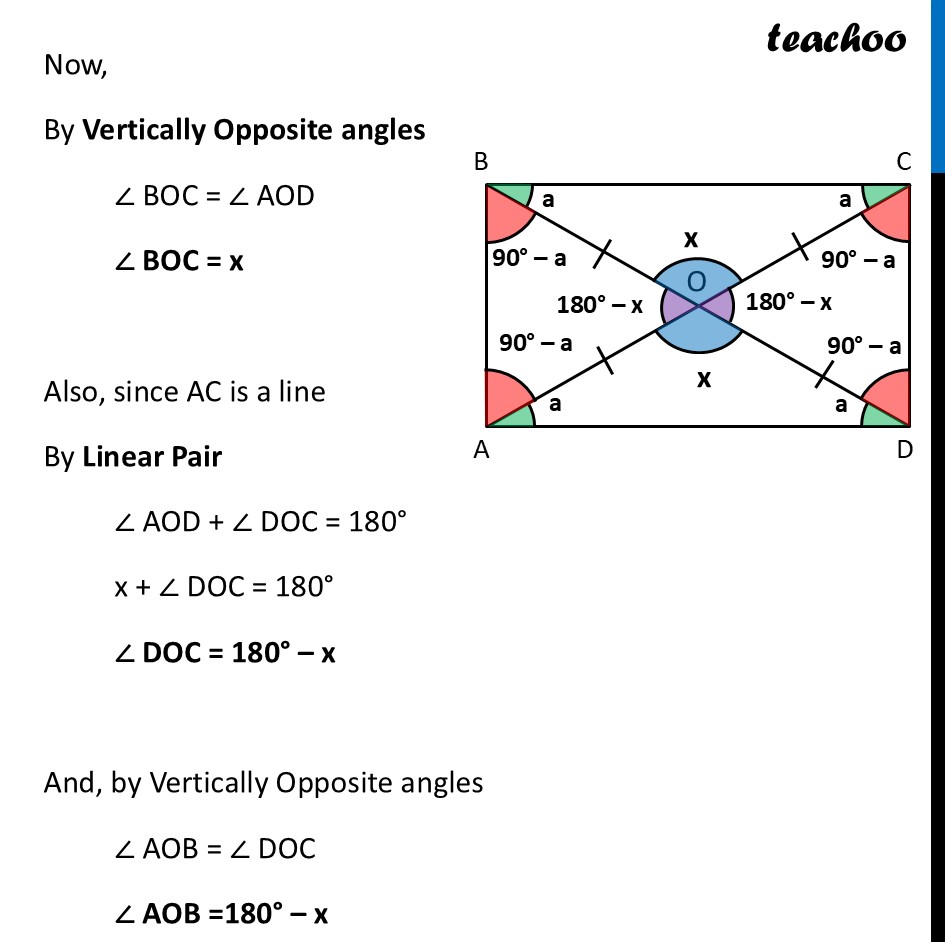
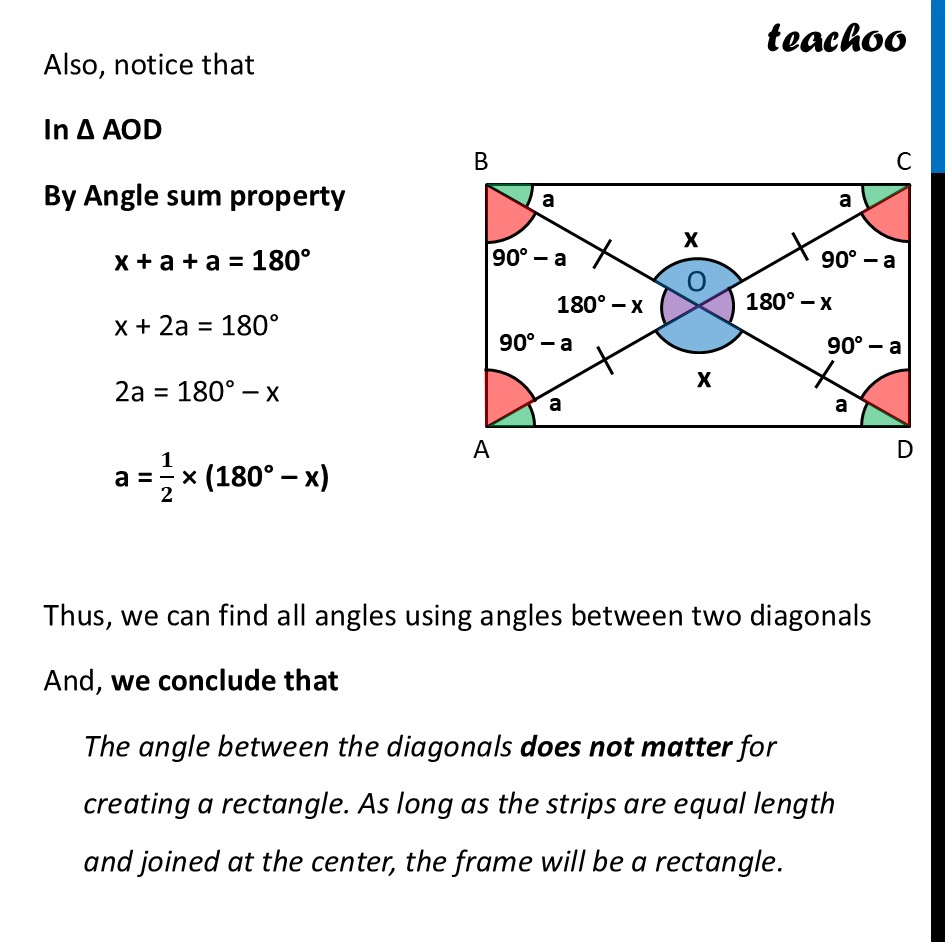
Deduction 3 What are the angles between the diagonals?Let’s assume ∠ AOD = x We find all other angles Since both diagonals are equal Since O is mid-point of AC OA = OC = 4 cm And, O is mid-point of BD OB = OD = 4 cm Thus, OA = OB = OC = OD = 4 cm Now, in ∆ AOD OA = OD And, we have an Isosceles Triangle property Which says Angles opposite to equal sides are equal ∴ ∠ OAD = ∠ ODA Let that angle be a ∴ ∠ OAD = ∠ ODA = a Since ∠ A = 90° Thus, ∠ BAO + ∠ OAD = 90° ∠ BAO + a = 90° ∠ BAO = 90° – a Similarly, ∠ CDO = 90° – a Now, applying Isosceles Triangle Property in ∆ AOB ∠ OBA = 90° – a Similarly Isosceles Triangle Property in ∆ AOB ∠ OCD = 90° – a Similarly, Since ∠ B = 90° Thus, ∠ ABO + ∠ OBC = 90° 90° – a + ∠ OBC = 90° ∠ OBC = 90° – 90° + a ∠ OBC = a Similarly, ∠ OCB = a Now, we need to find angles at the center Now, By Vertically Opposite angles ∠ BOC = ∠ AOD ∠ BOC = x Also, since AC is a line By Linear Pair ∠ AOD + ∠ DOC = 180° x + ∠ DOC = 180° ∠ DOC = 180° – x And, by Vertically Opposite angles ∠ AOB = ∠ DOC ∠ AOB =180° – x Also, notice that In ∆ AOD By Angle sum property x + a + a = 180° x + 2a = 180° 2a = 180° – x a = 𝟏/𝟐 × (180° – x) Thus, we can find all angles using angles between two diagonals And, we conclude that The angle between the diagonals does not matter for creating a rectangle. As long as the strips are equal length and joined at the center, the frame will be a rectangle.