Deduction 2 - What is the point of intersection of the two diagonals?

Transcript

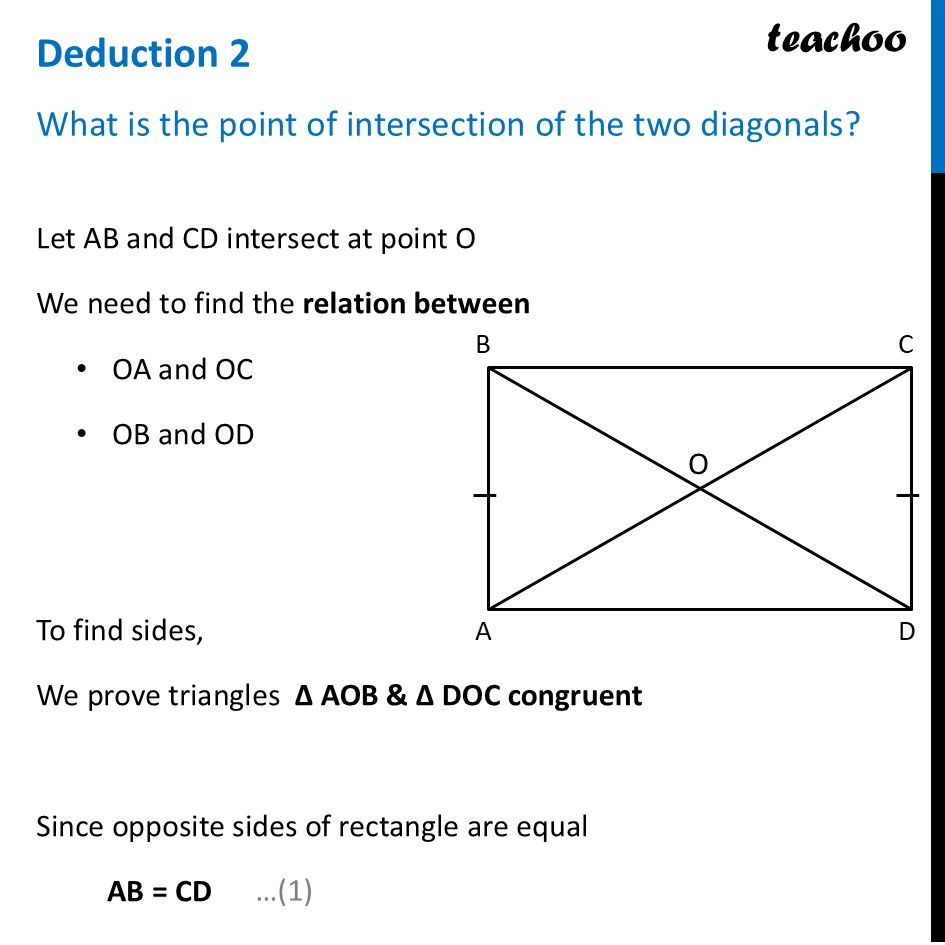
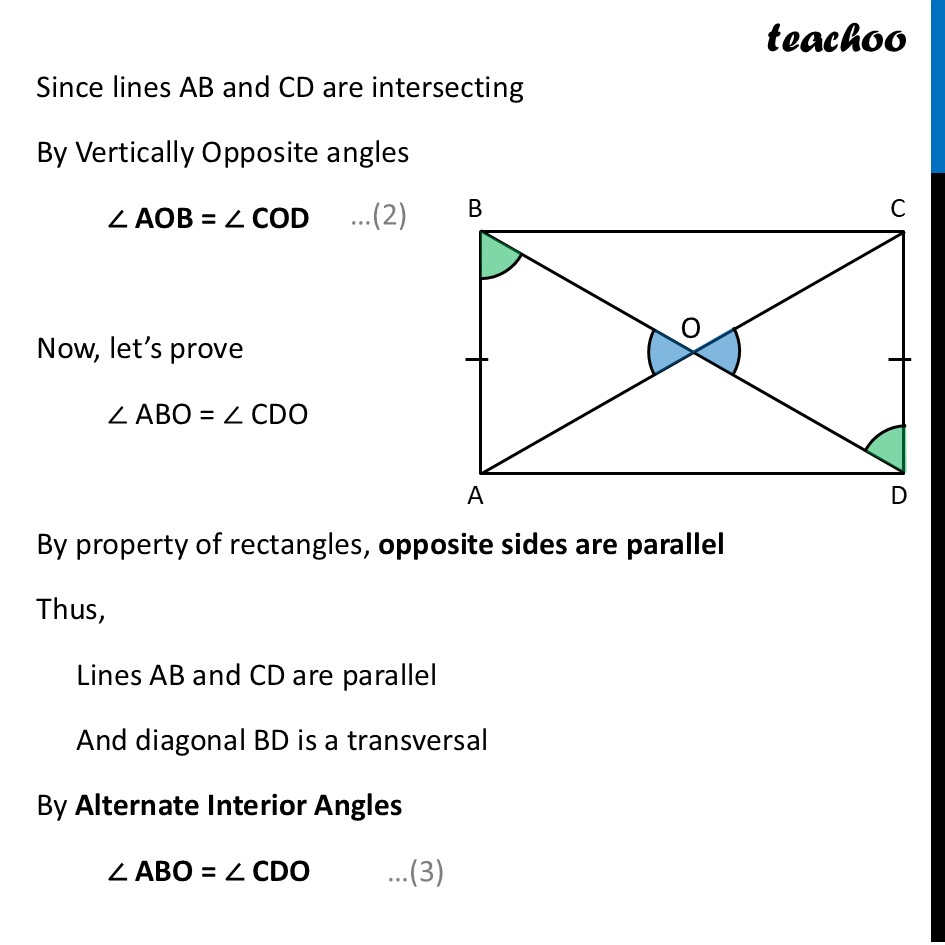
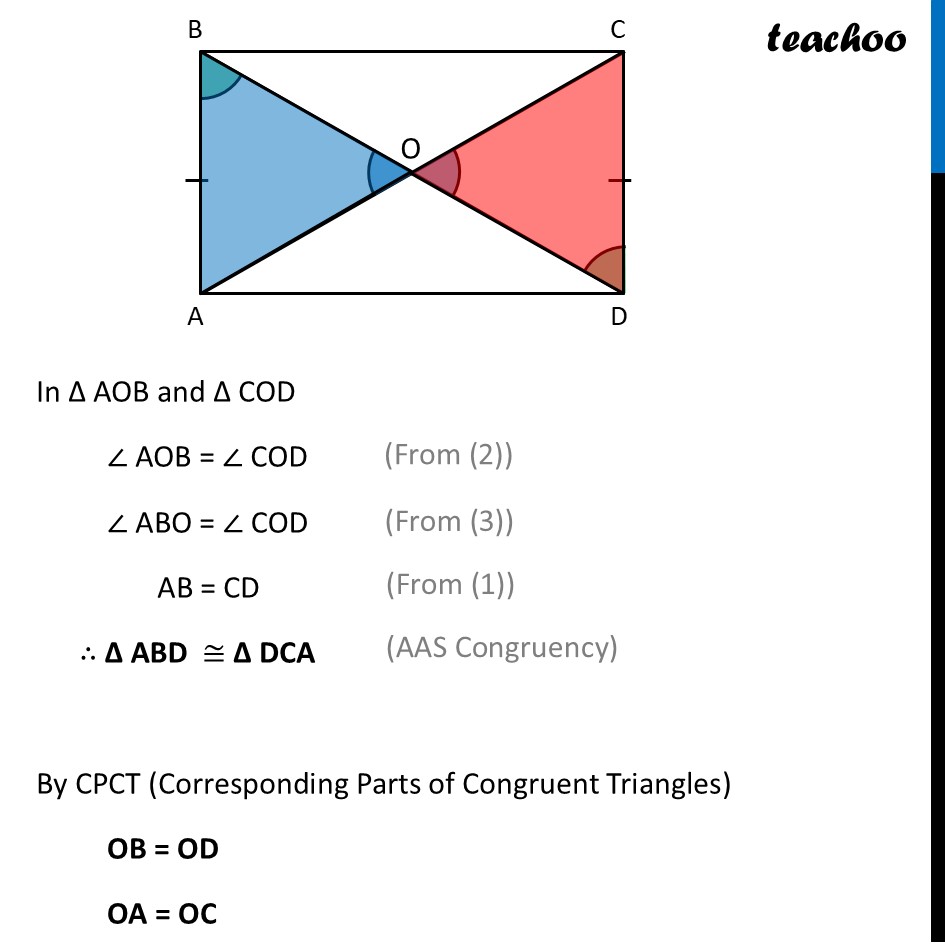
Deduction 2 What is the point of intersection of the two diagonals?Let AB and CD intersect at point O We need to find the relation between OA and OC OB and OD To find sides, We prove triangles ∆ AOB & ∆ DOC congruent Since opposite sides of rectangle are equal AB = CD Since lines AB and CD are intersecting By Vertically Opposite angles ∠ AOB = ∠ COD Now, let’s prove ∠ ABO = ∠ CDO By property of rectangles, opposite sides are parallel Thus, Lines AB and CD are parallel And diagonal BD is a transversal By Alternate Interior Angles ∠ ABO = ∠ CDO In ∆ AOB and ∆ COD ∠ AOB = ∠ COD ∠ ABO = ∠ COD AB = CD ∴ ∆ ABD ≅ ∆ DCA By CPCT (Corresponding Parts of Congruent Triangles) OB = OD OA = OC Thus, we can say O is mid-point of AC O is mid-point of BD This shows that the diagonals of a rectangle always intersect at their midpoints. Thus, point of intersection of the two diagonal is at their mid-point Note: When the diagonals cross at their midpoints, we say that the diagonals bisect each other. Bisecting a quantity means dividing it into two equal parts.