Question 2 - Figure it out (Page 54) - The Mechanism of Counting - Chapter 3 Class 8 - A Story of Numbers (Ganita Prakash)

Transcript

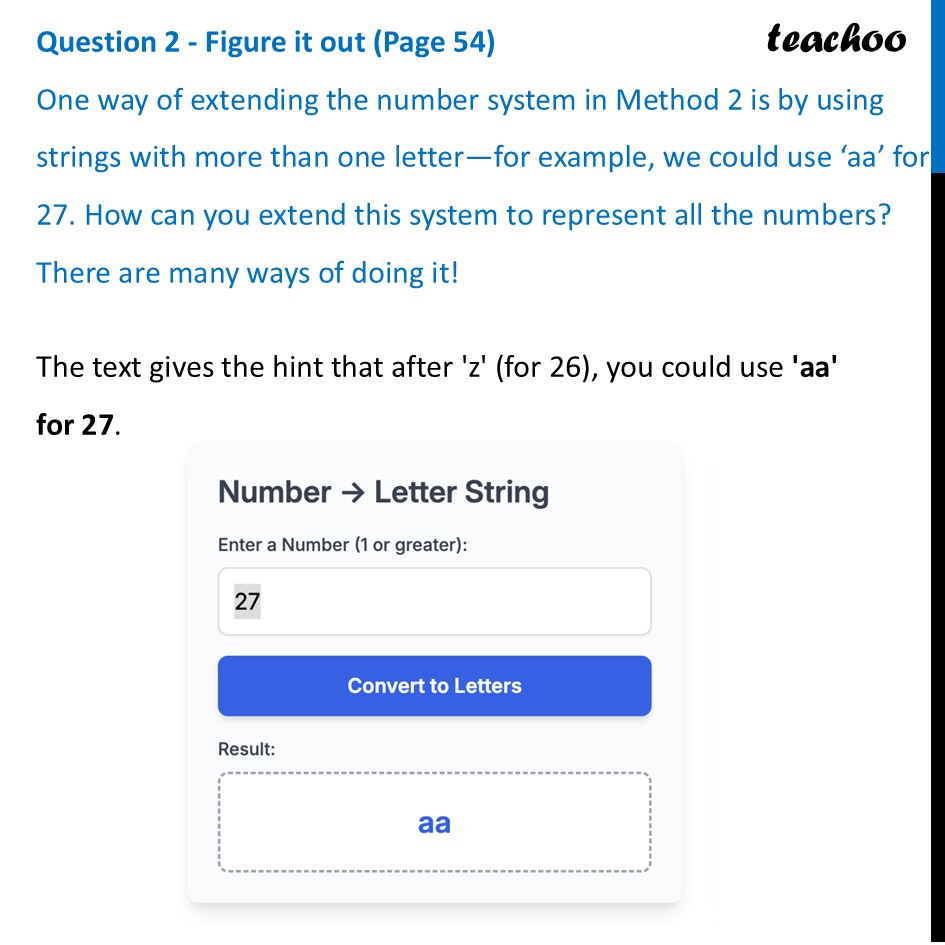
Question 2 - Figure it out (Page 54) One way of extending the number system in Method 2 is by using strings with more than one letter—for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!The text gives the hint that after 'z' (for 26), you could use 'aa' for 27. The text gives the hint that after 'z' (for 26), you could use 'aa' for 27. This hint reveals that the system can be extended by turning it into a base-26 place value system. This is very similar to how our base-10 system works. In our system, when we run out of single digits (at 9), we add a new position (the "tens" place) and start over: 10. In this alphabet system, you run out of single digits at 'z' (26). To represent the next number (27), you add a new "place" to the left. This new place represents groups of 26. The letter 'a' stands for 1, 'b' for 2, ..., and 'z' for 26. The numeral 'aa' means: (one × 26) + (one × 1) = 26 + 1 = 27. The numeral 'ab' would be: (one × 26) + (two × 1) = 26 + 2 = 28. ... The numeral 'az' would be: (one × 26) + (twenty-six × 1) = 26 + 26 = 52. The numeral 'ba' would be: (two × 26) + (one × 1) = 52 + 1 = 53. Using this method, you can represent any number. For example, when you run out of two-letter combinations (at 'zz'), you would simply add a third position ('aaa'), which would represent the "26 × 26" (or 676) place.