Observations in a Magic Square

Transcript

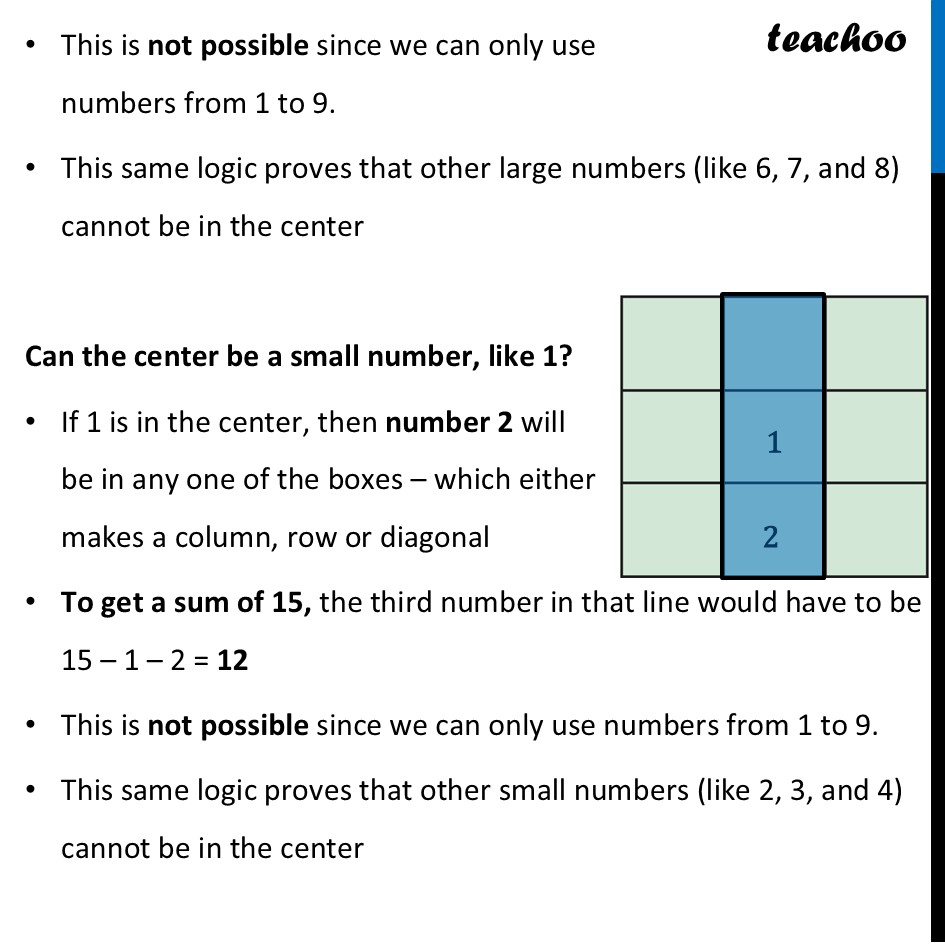
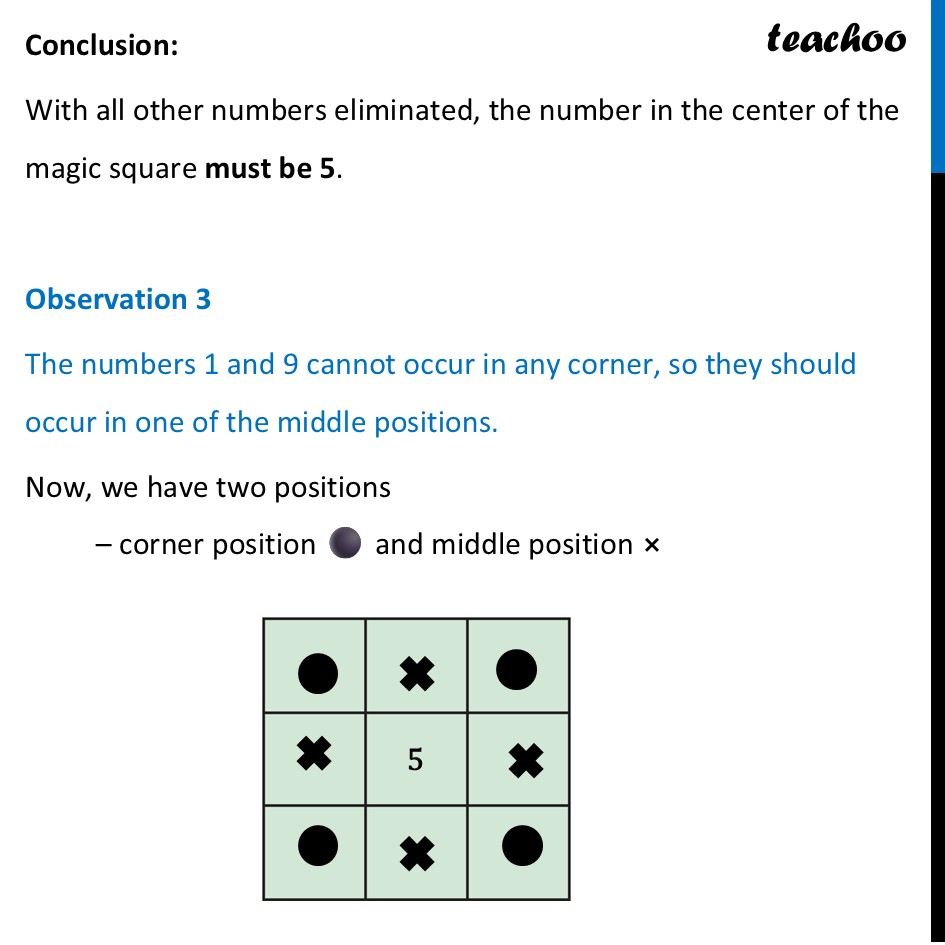
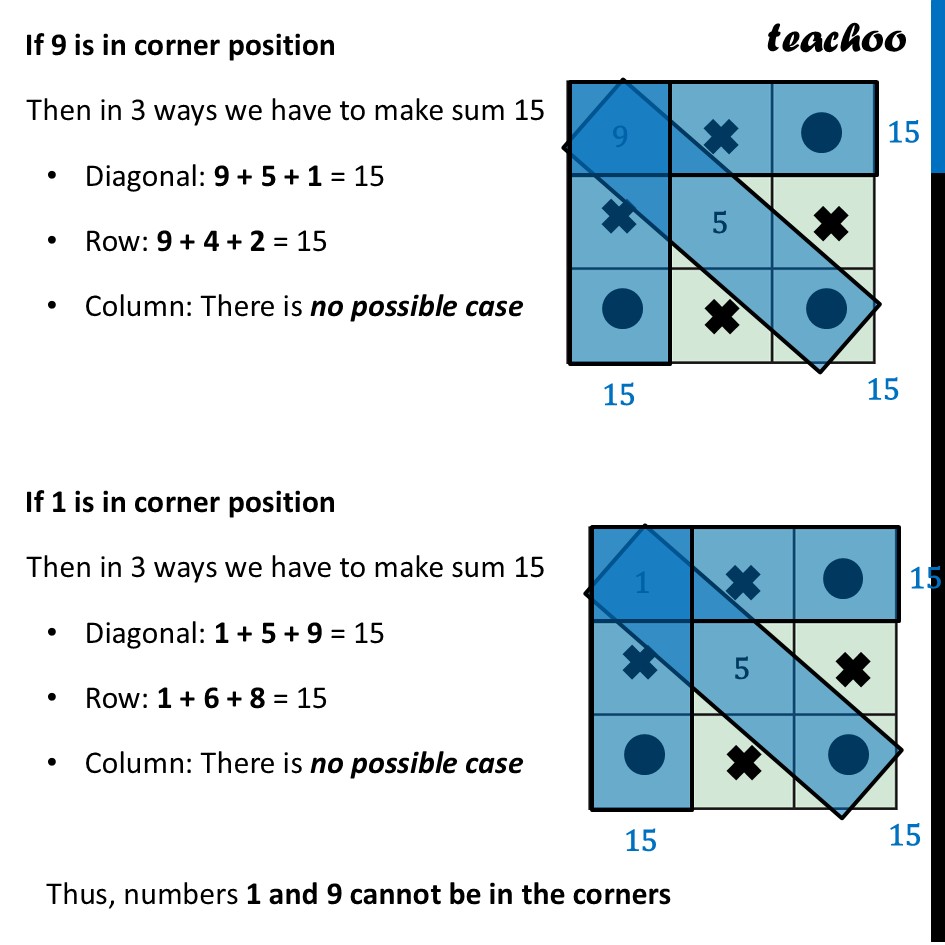
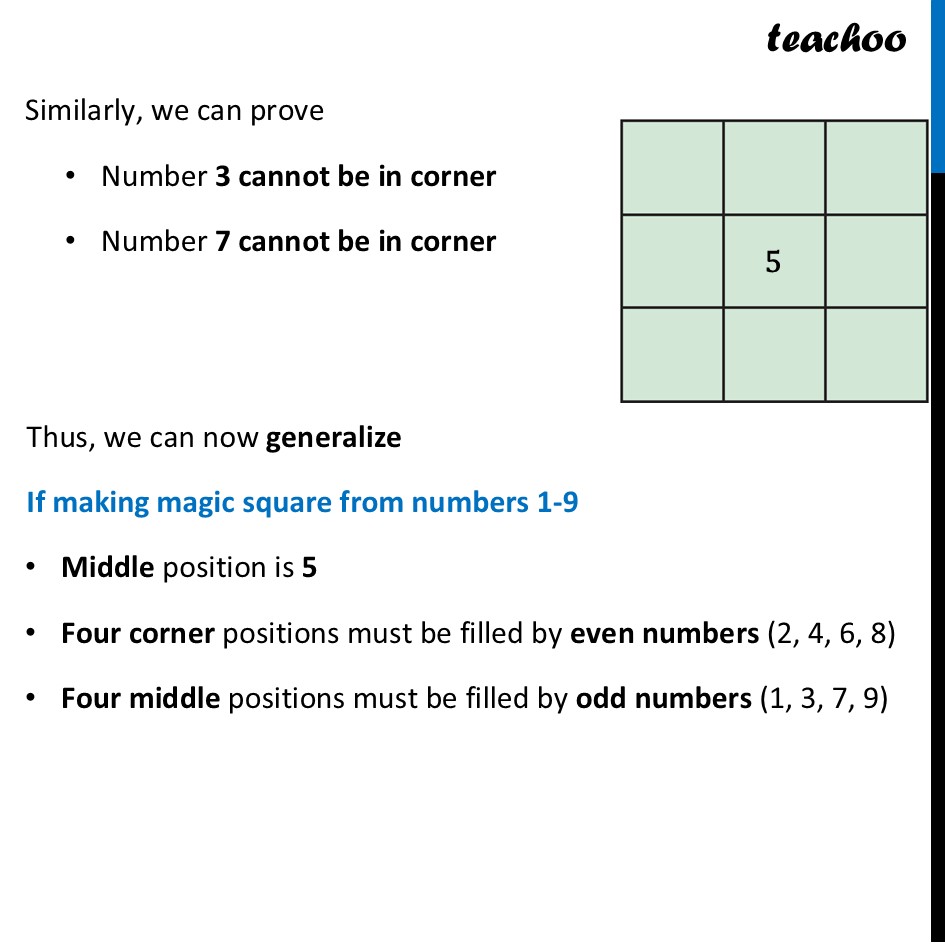
Observations in a Magic Square In Magic square, Sum of all rows, columns, diagonals are same Observation 1 In a magic square made using the numbers 1 – 9, the magic sum must be 15 Let’s figure out what the magic sum has to be The grid uses every number from 1 to 9 exactly once The sum of all these numbers is 1+2+3+4+5+6+7+8+9=45 This total of 45 is spread across three rows, and each row must have the same sum Therefore, the sum of each row—and thus the magic sum—must be 45 ÷ 3 = 15 Similarly, we can prove for columns Conclusion: Any 3 × 3 magic square using the numbers 1-9 will have a magic sum of 15. Observation 2 The number occurring at the centre of a magic square, filled using 1 – 9, must be 5 Can the center be a large number, like 9? If 9 is in the center, then number 8 will be in any one of the boxes – which either makes a column, row or diagonal To get a sum of 15, the third number in that line would have to be 15 – 9 – 8 = –2 This is not possible since we can only use numbers from 1 to 9. This same logic proves that other large numbers (like 6, 7, and 8) cannot be in the center Can the center be a small number, like 1? If 1 is in the center, then number 2 will be in any one of the boxes – which either makes a column, row or diagonal To get a sum of 15, the third number in that line would have to be 15 – 1 – 2 = 12 This is not possible since we can only use numbers from 1 to 9. This same logic proves that other small numbers (like 2, 3, and 4) cannot be in the center Conclusion: With all other numbers eliminated, the number in the center of the magic square must be 5. Observation 3 The numbers 1 and 9 cannot occur in any corner, so they should occur in one of the middle positions. Now, we have two positions – corner position ⚫️ and middle position ⨯ If 9 is in corner position Then in 3 ways we have to make sum 15 Diagonal: 9 + 5 + 1 = 15 Row: 9 + 4 + 2 = 15 Column: There is no possible case If 1 is in corner position Then in 3 ways we have to make sum 15 Diagonal: 1 + 5 + 9 = 15 Row: 1 + 6 + 8 = 15 Column: There is no possible case Thus, numbers 1 and 9 cannot be in the corners Similarly, we can prove Number 3 cannot be in corner Number 7 cannot be in corner Thus, we can now generalize If making magic square from numbers 1-9 Middle position is 5 Four corner positions must be filled by even numbers (2, 4, 6, 8) Four middle positions must be filled by odd numbers (1, 3, 7, 9)