You are here
Perfect Squares and Odd Numbers
Last updated at July 29, 2025 by Teachoo
Class 8 (Ganita Prakash & Old NCERT)
Chapter 1 Class 8 - A Square and a Cube (Ganita Prakash)
- Introduction
- Square Numbers
- Perfect Squares - and its Properties
-
Perfect Squares - and its Patterns
- Square Root
- Smallest number multiply or divide to get perfect square
- Estimating Square Root
- Figure it out - Page 10, 11
- Cubic Numbers
- Perfect Cubes - and its Properties
- Perfect Cubes - and its Patterns
- Cube Root
- Smallest number multiply or divide to get perfect cube
- A pinch of History
- Figure it out - Page 16, 17
Transcript
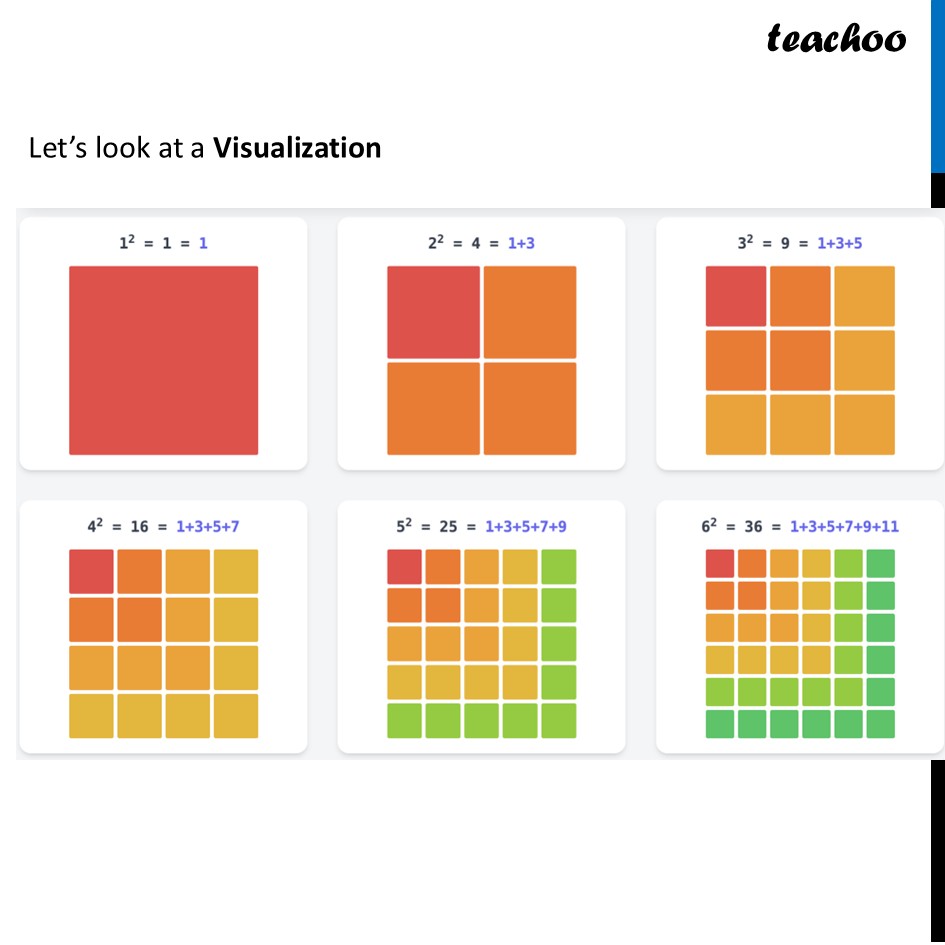
Perfect Squares and Odd Numbers There is a fundamental pattern connecting perfect squares and odd numbers: Every perfect square is the sum of consecutive odd numbers starting from 1. Thus, β΄ Sum of n Odd Number = π^π Testing for a Perfect Square This relationship provides a method to check if a number is a perfect square. You can do this by successively subtracting odd numbers starting from 1. If you reach exactly 0, the number is a perfect square. The number of subtractions you performed is its square root. Example For 25: 25 β 1 = 24 24 β 3 = 21 21 β 5 = 16 16 β 7 = 9 9 β 9 = 0 Letβs look at a Visualization Since we subtracted 5 odd numbers, 25 = 52 Note: If you pass 0 and get a negative number, the number is not a perfect square because it cannot be expressed as a sum of successive odd numbers.
