Ex 7.1,14 - Chapter 7 Class 11 Binomial Theorem

Transcript

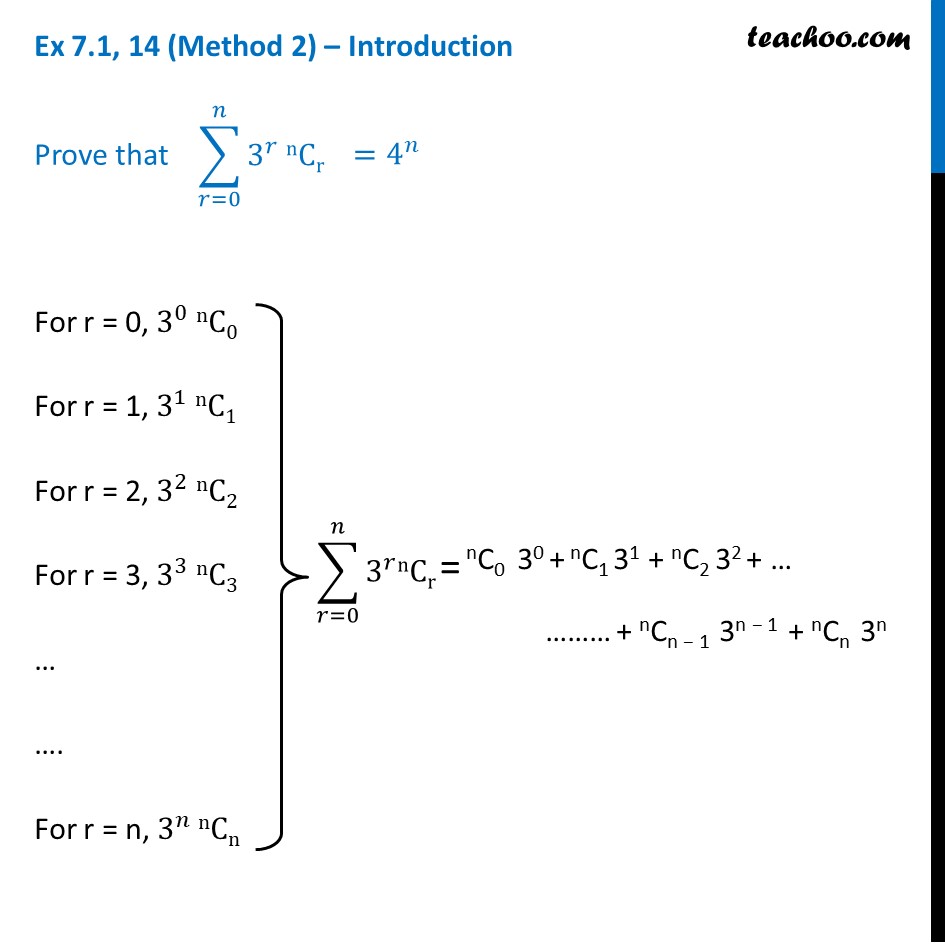
Ex 7.1, 14 (Method 1) By Binomial Theorem, Putting b = 3 and a = 1 in the above equation Prove that ∑_(𝑟=0)^𝑛▒〖3^𝑟 nCr〗 ∑_(𝑟=0)^𝑛▒nCr 𝑎^(𝑛 − 𝑟) 𝑏^𝑟 ∑_(𝑟=0)^𝑛▒nCr 1^(𝑛−𝑟) 3^𝑟 Hence proved Ex 7.1, 14 (Method 2) – Introduction For r = 0, 3^0 nC0 For r = 1, 3^1 nC1 For r = 2, 3^2 nC2 For r = 3, 3^3 nC3 … …. For r = n, 3^𝑛 nCn nC0 30 + nC1 31 + nC2 32 + … ……… + nCn − 1 3n − 1 + nCn 3n Prove that = nC0 30 + nC1 31 + nC2 32 + ……………… + nCn-1 3n-1 + nCn 3n Ex 7.1, 14(Method 2) Solving L.H.S This is similar to nC0 an b0 + nC1 an-1 b1 + nC2 an-2 b2 + …… .+ nCn-1 a1 bn-1 + nCn a0 bn Where a = 1 , b = 3 And we know that (a + b)n = nC0 an b0 + nC1 an-1 b1 + …….+ nCn-1 a1 bn-1 + nCn a0 bn = (1 + 3)n = (4)n = R.H.S Hence proved