Question 5 - Area of combination of figures : sector based - Chapter 11 Class 10 Areas related to Circles

Transcript

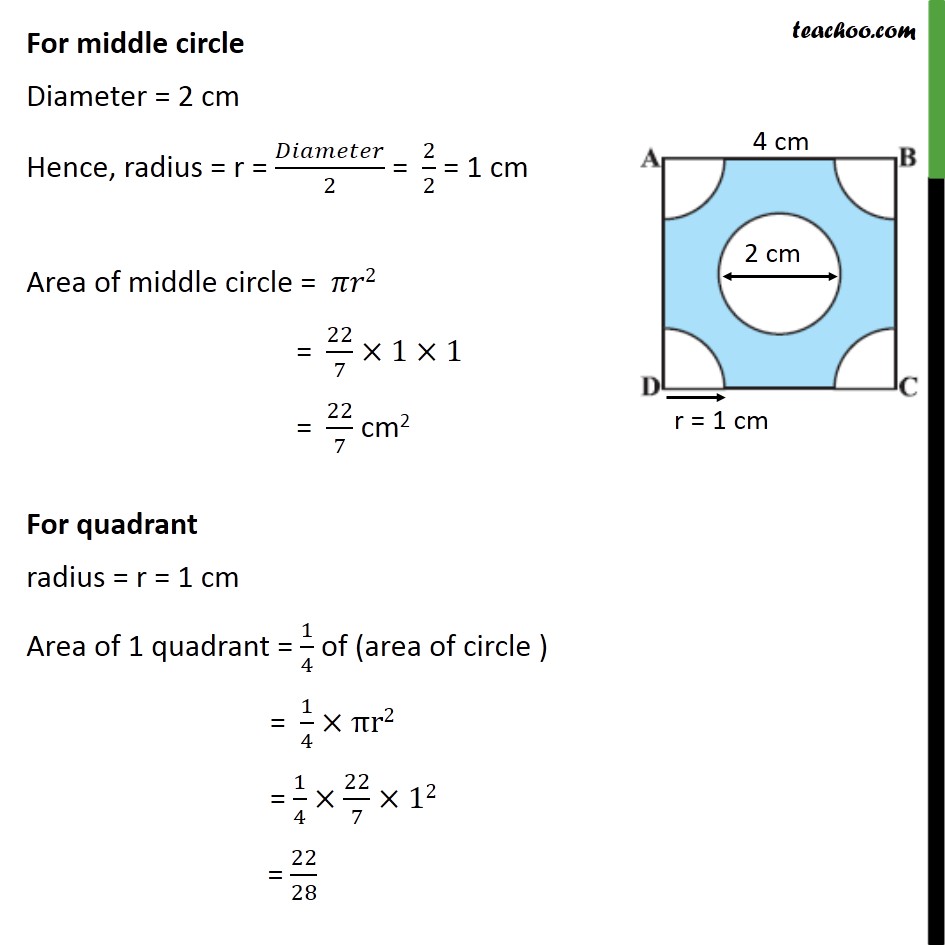
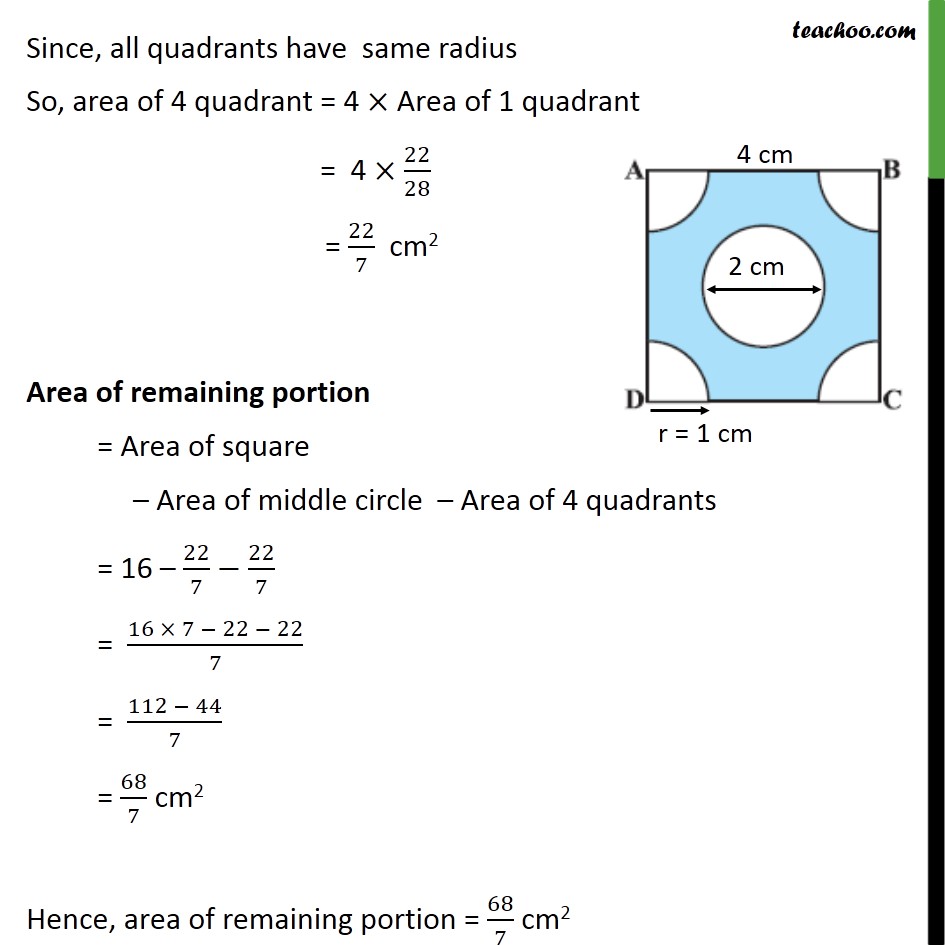
Question 5 From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the square. Area of remaining portion = Area of square – Area of middle circle – Area of 4 quadrants For square ABCD Area of square = (side)2 = (4)2 = 4 × 4 = 16 For middle circle Diameter = 2 cm Hence, radius = r = 𝐷𝑖𝑎𝑚𝑒𝑡𝑒𝑟/2 = 2/2 = 1 cm Area of middle circle = 𝜋𝑟2 = 22/7×1×1 = 22/7 cm2 For quadrant radius = r = 1 cm Area of 1 quadrant = 1/4 of (area of circle ) = 1/4×πr2 = 1/4×22/7×12 = 22/28 Since, all quadrants have same radius So, area of 4 quadrant = 4 × Area of 1 quadrant = 4 × 22/28 = 22/7 cm2 Area of remaining portion = Area of square – Area of middle circle – Area of 4 quadrants = 16 – 22/7−22/7 = (16 × 7 − 22 − 22)/7 = (112 − 44)/7 = 68/7 cm2 Hence, area of remaining portion = 68/7 cm2