Ex 11.1, 13 - Chapter 11 Class 10 Areas related to Circles

Transcript

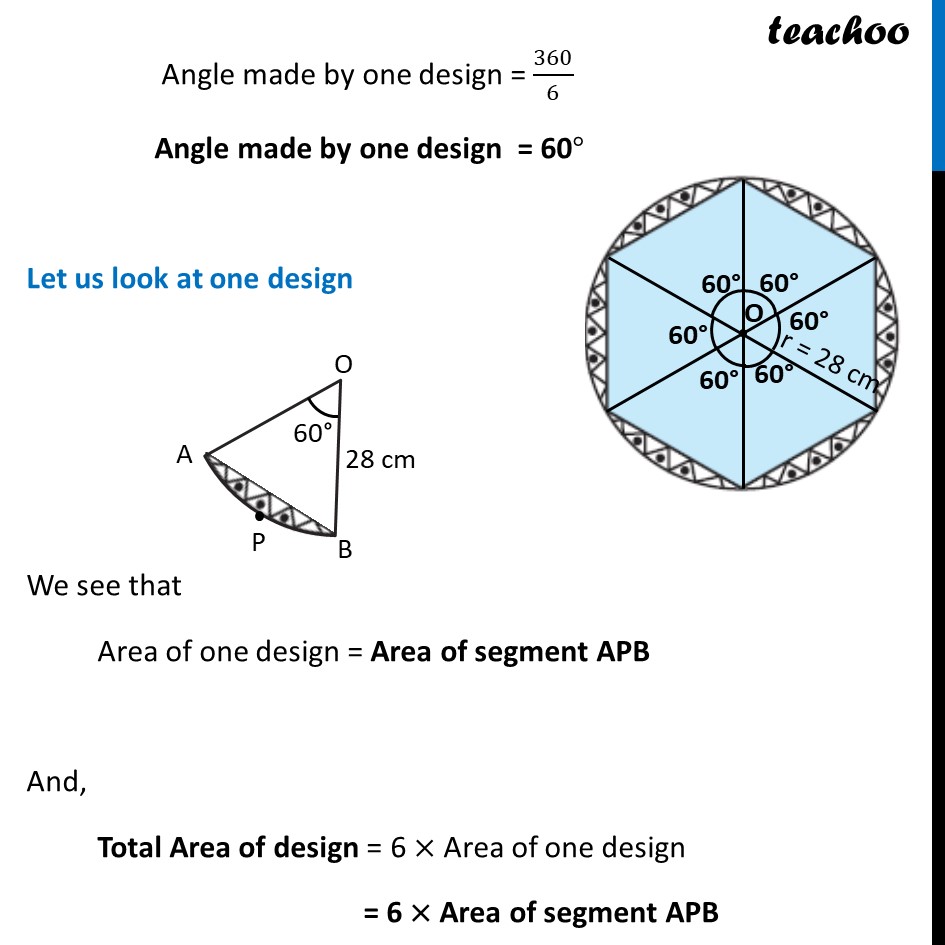
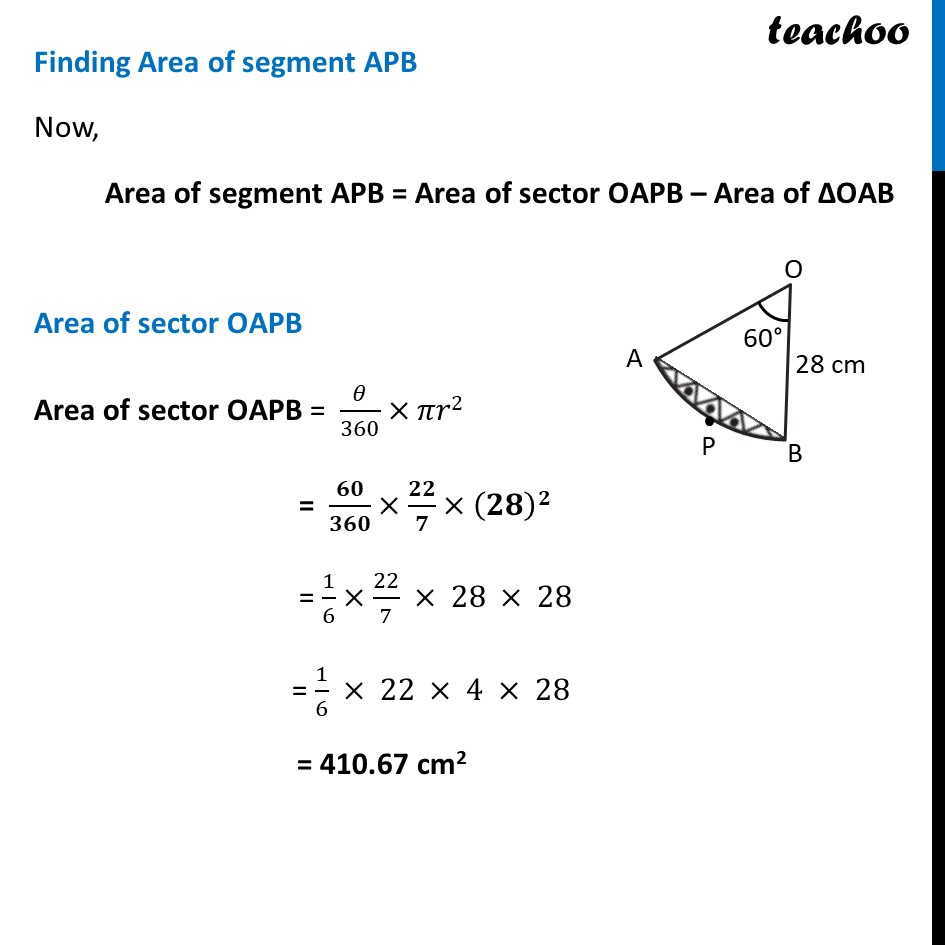
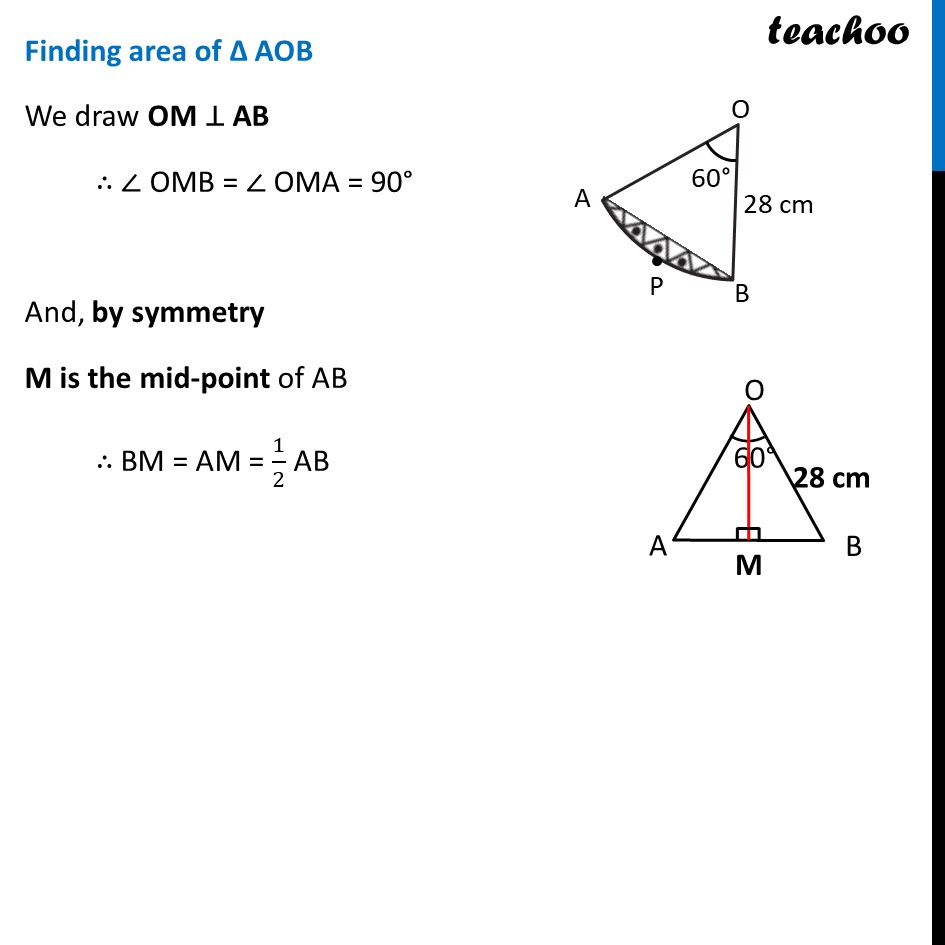
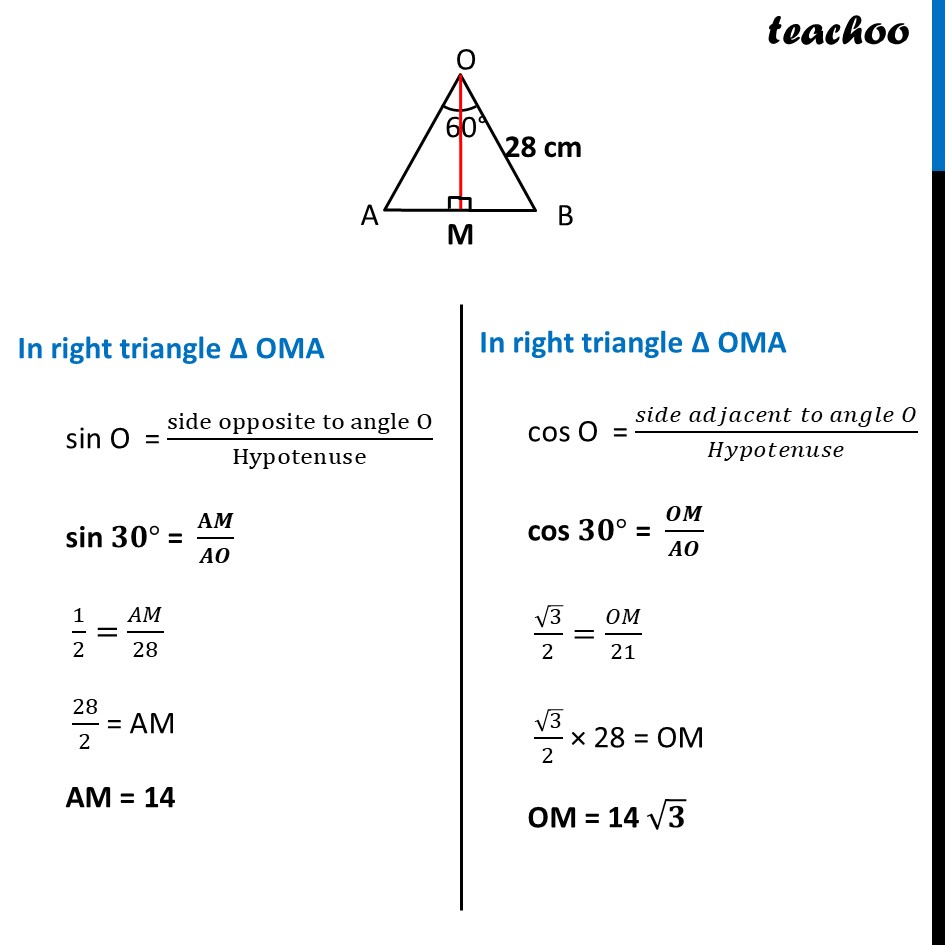
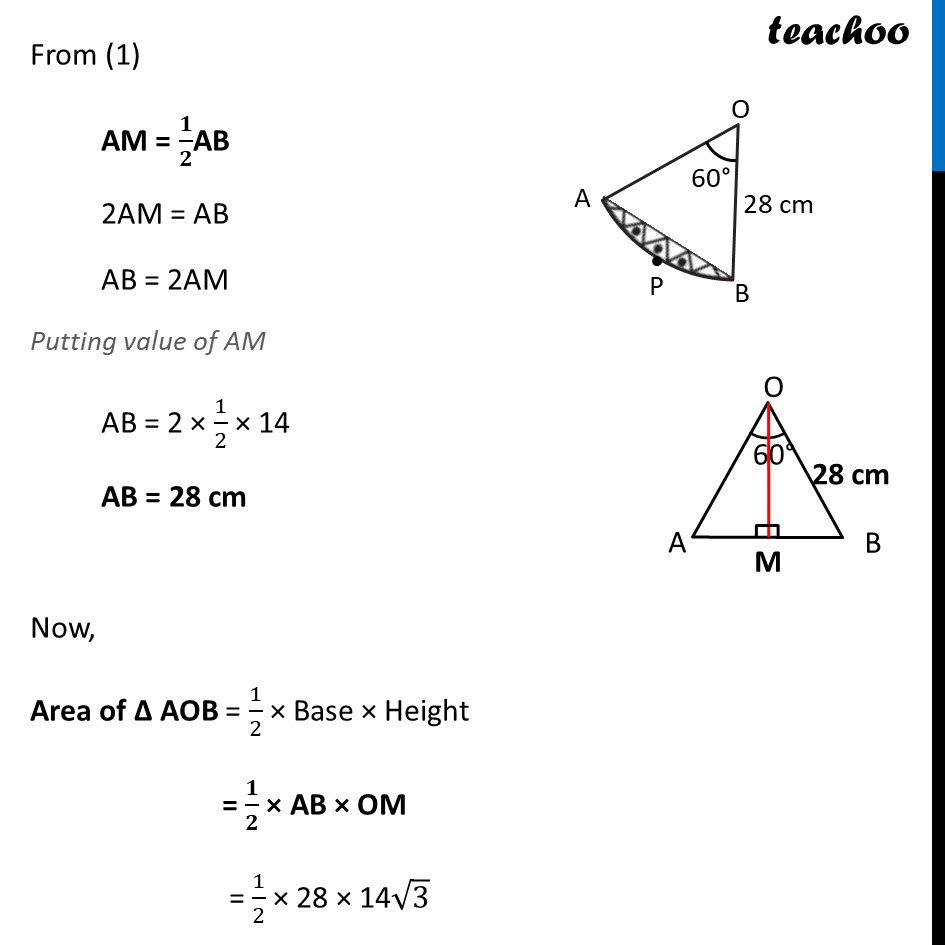
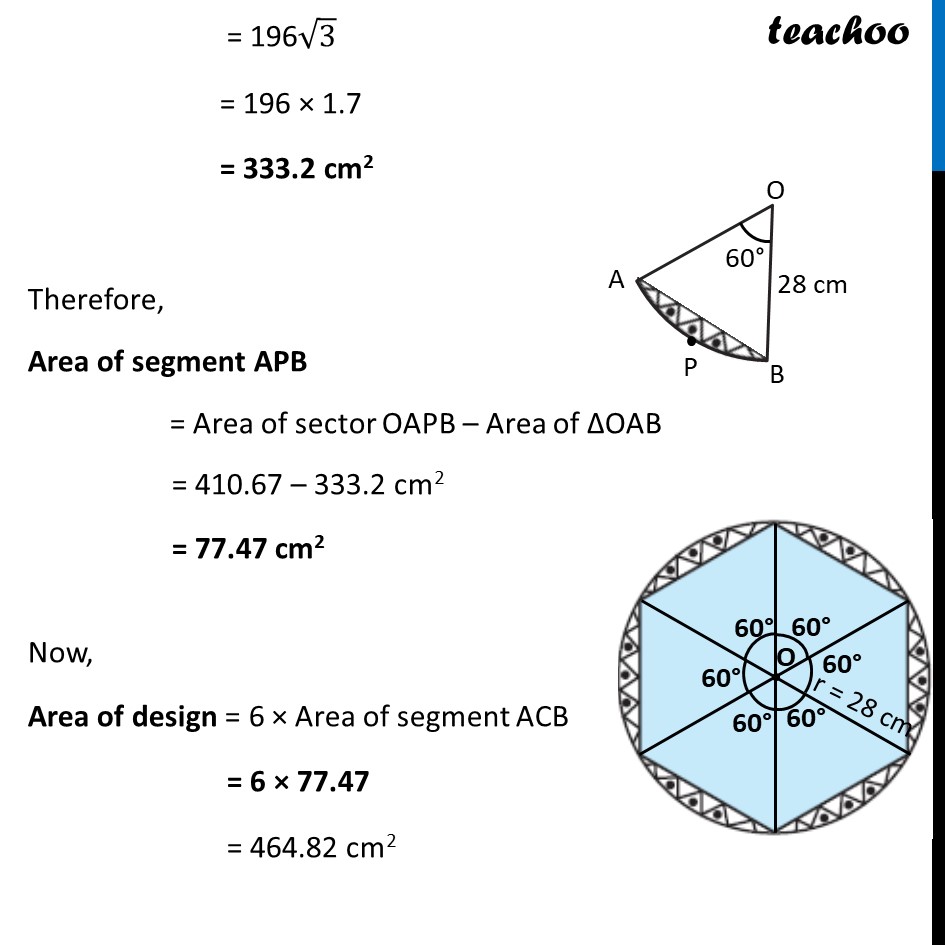
Ex 11.1, 13 A round table cover has six equal designs as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2. (Use √3 = 1.7) In the question a round table cover is given which has six equal designs. Let us join ends of the design Since the designs are equal, the angle made by the designs at point O will be equal. We know that Sum of angles at a point = 360° 6 × Angle made by one design = 360° Angle made by one design = 360/6 Angle made by one design = 60° Let us look at one design We see that Area of one design = Area of segment APB And, Total Area of design = 6 × Area of one design = 6 × Area of segment APB Finding Area of segment APB Now, Area of segment APB = Area of sector OAPB – Area of ΔOAB Area of sector OAPB Area of sector OAPB = 𝜃/360×𝜋𝑟2 = 𝟔𝟎/𝟑𝟔𝟎×𝟐𝟐/𝟕×(𝟐𝟖)𝟐 = 1/6×22/7 × 28 × 28 = 1/6 × 22 × 4 × 28 = 410.67 cm2 Finding area of Δ AOB We draw OM ⊥ AB ∴ ∠ OMB = ∠ OMA = 90° And, by symmetry M is the mid-point of AB ∴ BM = AM = 1/2 AB In right triangle Δ OMA sin O = (side opposite to angle O)/Hypotenuse sin 𝟑𝟎° = 𝐀𝑴/𝑨𝑶 1/2=𝐴𝑀/28 28/2 = AM AM = 14 In right triangle Δ OMA cos O = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑂)/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 cos 𝟑𝟎° = 𝑶𝑴/𝑨𝑶 √3/2=𝑂𝑀/21 √3/2 × 28 = OM OM = 14 √𝟑 From (1) AM = 𝟏/𝟐AB 2AM = AB AB = 2AM Putting value of AM AB = 2 × 1/2 × 14 AB = 28 cm Now, Area of Δ AOB = 1/2 × Base × Height = 𝟏/𝟐 × AB × OM = 1/2 × 28 × 14√3 = 196√3 = 196 × 1.7 = 333.2 cm2 Therefore, Area of segment APB = Area of sector OAPB – Area of ΔOAB = 410.67 – 333.2 cm2 = 77.47 cm2 Now, Area of design = 6 × Area of segment ACB = 6 × 77.47 = 464.82 cm2 We need to find cost of the design Finding Cost of the design Given that find the cost of making the designs at the rate of Rs 0.35 per cm2 Now, Cost of making 1 cm2 design = Rs 0.35 Cost of making 464.82 cm2 design = Rs 0.35 × 464.82 = Rs 162.68