Linear Pair of angles

Linear pair is a pair of adjacent angles where non-common side forms a straight line

So, In a linear pair, there are two angles who have

• Common vertex
• Common side
• Non-common side makes a straight line or Sum of angles is 180°

Linear pair

Linear pair is a pair of adjacent angles where non-common side forms a straight line

So, In a linear pair, there are two angles who have

• Common vertex
• Common side
• Non-common side makes a straight line or Sum of angles is 180°

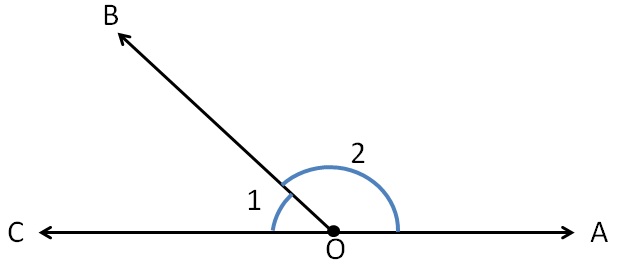
Here, these angles are in linear pair as

• They have common vertex O.
• They have common side OB
• Non Common side (AC) is a straight line.
  
  

Here,

  ∠1 + ∠2 = 180°

Sum of linear pair = 180°   

Let’s take this figure

In this figure

  ∠1 & ∠2 are linear pair

   ∠2 & ∠3 are linear pair

  ∠3 & ∠4 are linear pair

  ∠4 & ∠1 are linear pair

So,

     ∠1 + ∠2 = 180°

     ∠2 + ∠3 = 180°

     ∠3 + ∠4 = 180°

     ∠4 + ∠1 = 180°

Let’s take some more examples.

Do the angles form a linear pair?

Here,

  Angles have a common vertex O,

  They have a common side OB

Now,

  Sum of angles = 40° + 140°

   = 180°

  ∴ Non-common sides from a line

Hence, angles form a linear pair.

Do the angles form a linear pair?

Here,

Angles have a common vertex O,

They have a common side OB

But,

Non-common side of ∠1 and ∠2

Do not form a line

∴  They do not form a linear pair

Do the angles form a linear pair?

Here,

Angles have a common vertex O,

They have a common side OQ

Now,

  Sum of angles = 60° + 90°

   = 150°

   ≠ 180°

  ∴ Non-common sides do not form a line

Hence, angle do not form a linear pair

Do the angles form a linear pair?

Here,

Angle do not have  common vertex

∴ They do not form a linear pair

Do the angles form a linear pair?

Here,

Angles have a common vertex O,

They have a common base OB

Now,

  Sum of angles = 65° + 115° = 180°

Since sum of angles is 180°

∴ They form a linear pair