Question 5 - Constructing tangent from external point - Constructions

Transcript

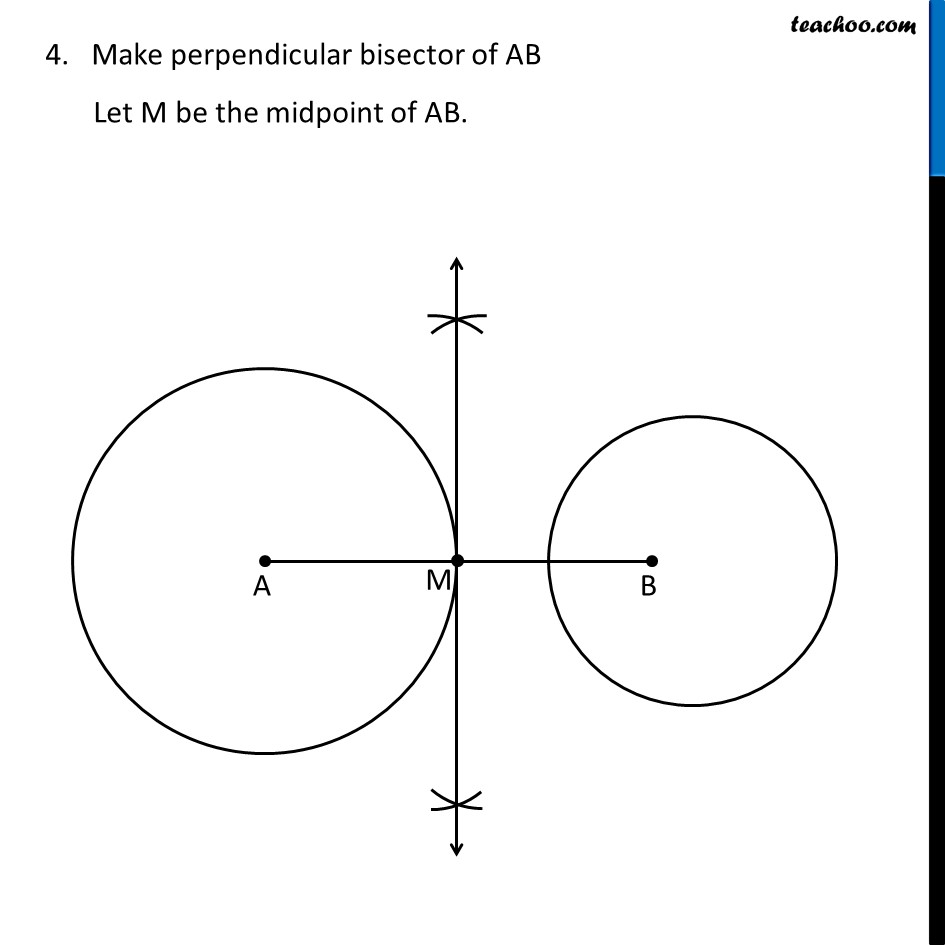
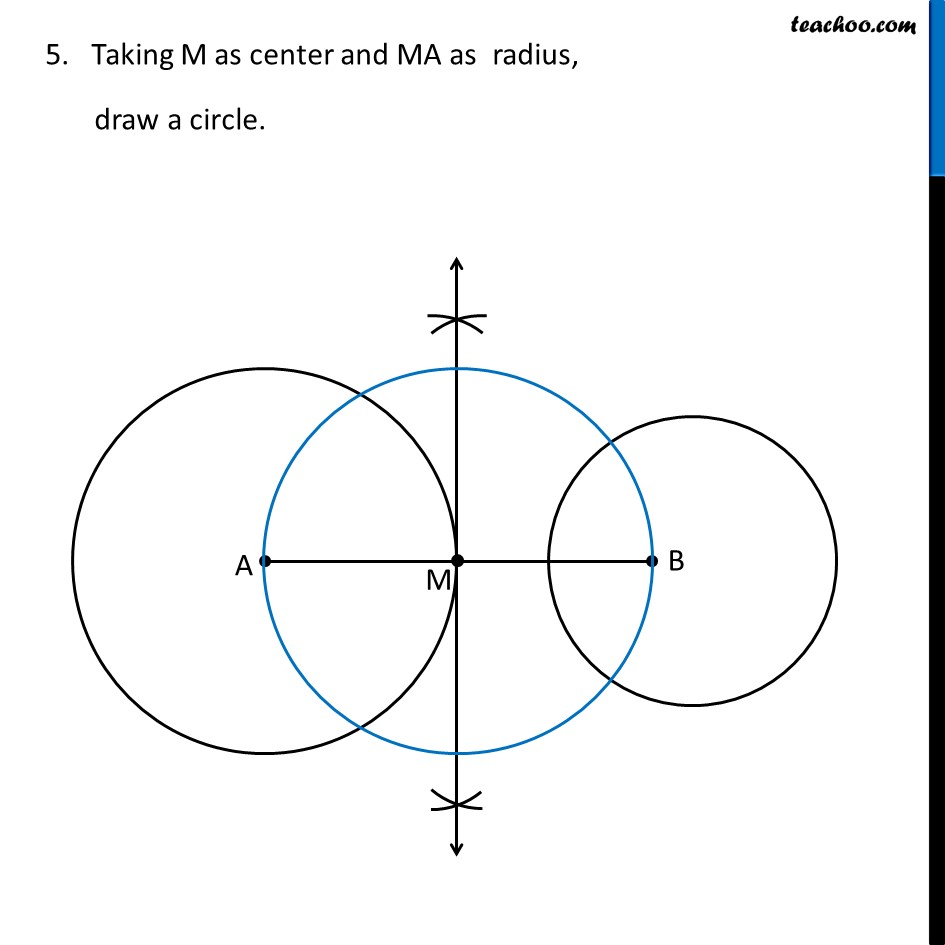
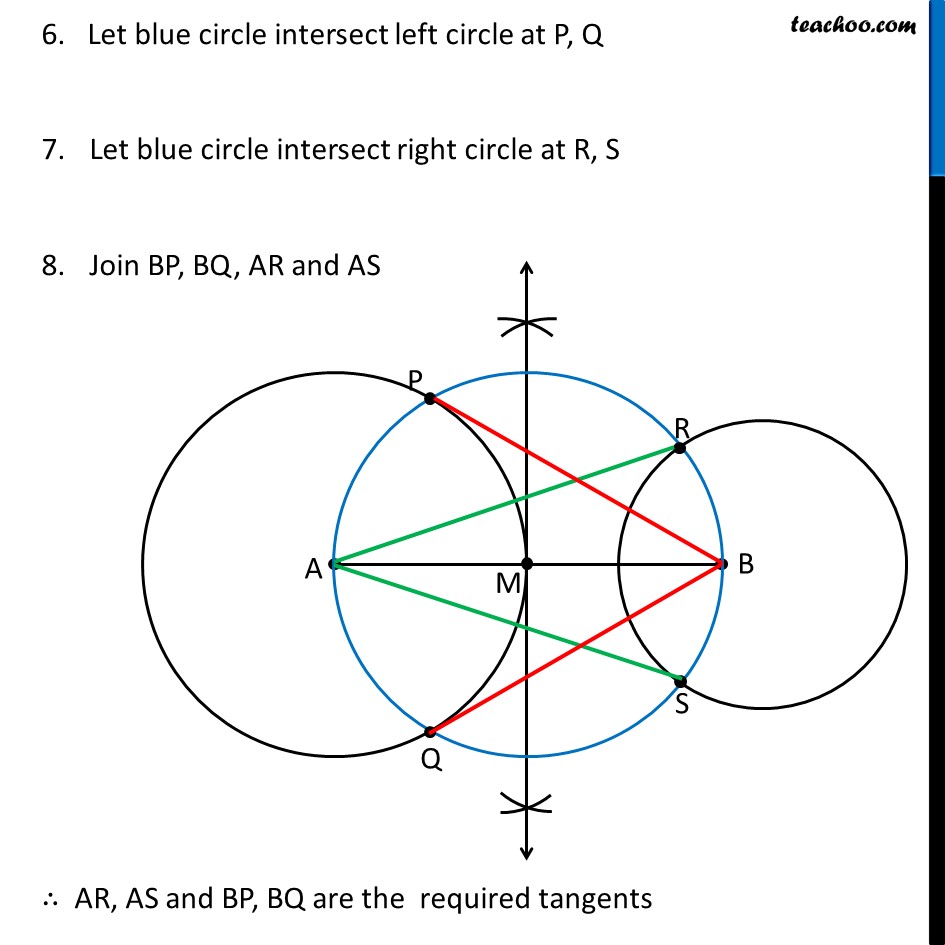
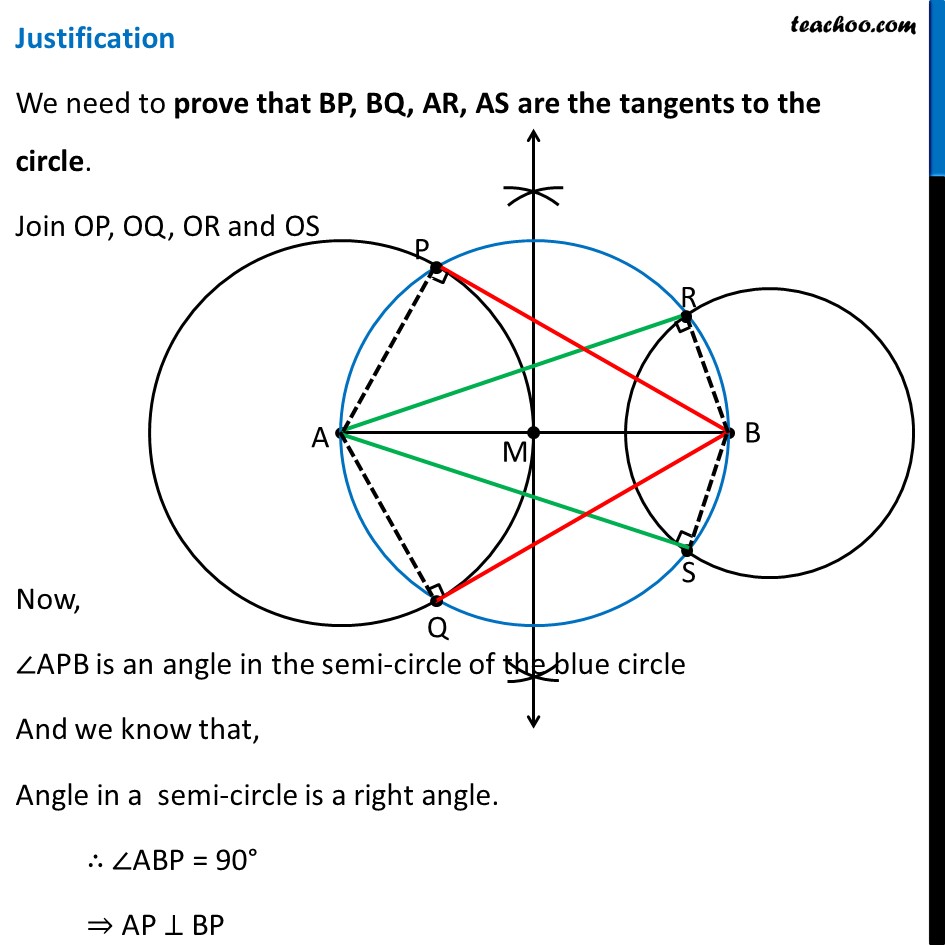
Question 5 Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. Steps of construction Draw line segment AB of length 8 cm Taking A as center, draw a circle of radius 4 cm Taking B as center, draw a circle of radius 3 cm Now, we need to draw tangent from point A to the right circle, and from point B to the left circle. To draw tangents to the right circle, we need to draw perpendicular bisector of line AB 4. Make perpendicular bisector of AB Let M be the midpoint of AB. 5. Taking M as center and MA as radius, draw a circle. 6. Let blue circle intersect left circle at P, Q Let blue circle intersect right circle at R, S Join BP, BQ, AR and AS ∴ AR, AS and BP, BQ are the required tangents Justification We need to prove that BP, BQ, AR, AS are the tangents to the circle. Join OP, OQ, OR and OS Now, ∠APB is an angle in the semi-circle of the blue circle And we know that, Angle in a semi-circle is a right angle. ∴ ∠ABP = 90° ⇒ AP ⊥ BP Since AP is the radius of the circle, BP has to be a tangent of the circle. Similarly, we can prove BQ, AR, AS are tangents of the circle.