Theorem 9.5 - Chapter 9 Class 9 Circles

Transcript

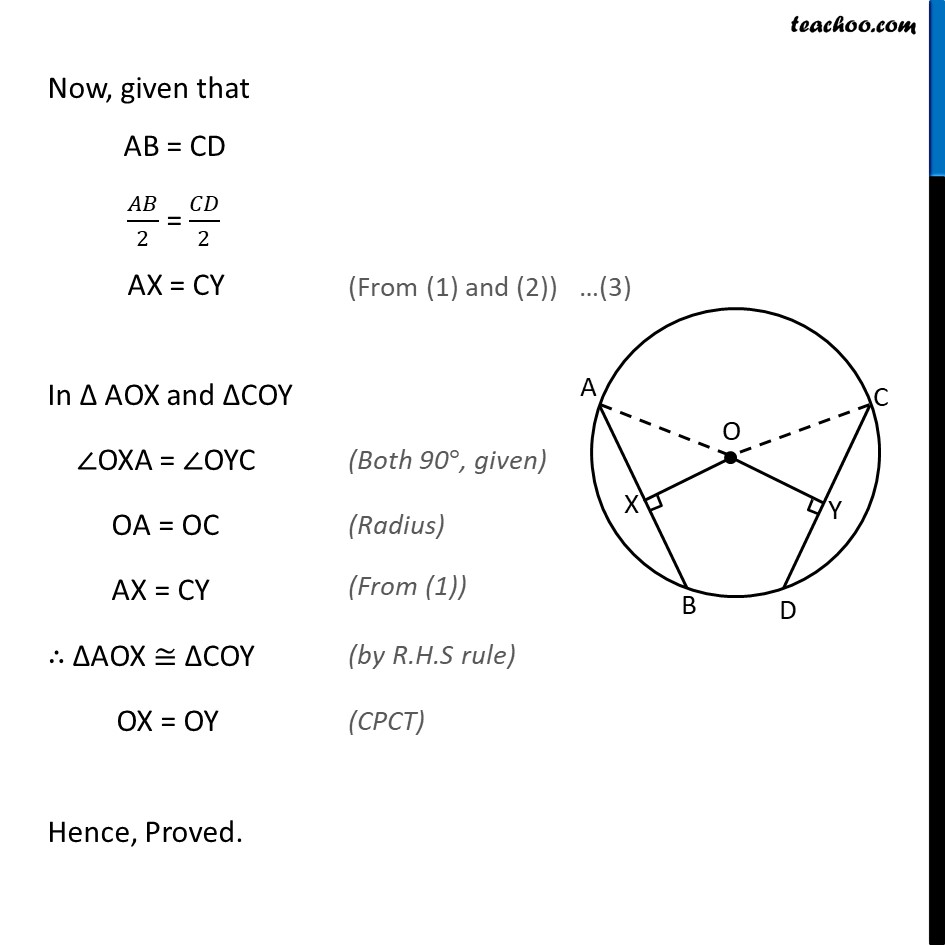
Theorem 9.6 Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres). Given : A circle with center at O. AB and CD are two equal chords of circle i.e. AB = CD & OX and OY are perpendiculars to AB & CD respectively. To Prove : OX = OY Proof : Since OX ⊥ AB Perpendicular from the center to the chord, bisects the chord AX = BX = (𝐴𝐵 )/2 Since OY ⊥ CD Perpendicular from the center to the chord, bisects the chord CY = DY = (𝐶𝐷 )/2 Now, given that AB = CD 𝐴𝐵/2 = 𝐶𝐷/2 AX = CY In ∆ AOX and ∆COY ∠OXA = ∠OYC OA = OC AX = CY ∴ ∆AOX ≅ ∆COY OX = OY Hence, Proved.