Ex 14.2, 8 - Chapter 14 Class 11 Probability

Transcript

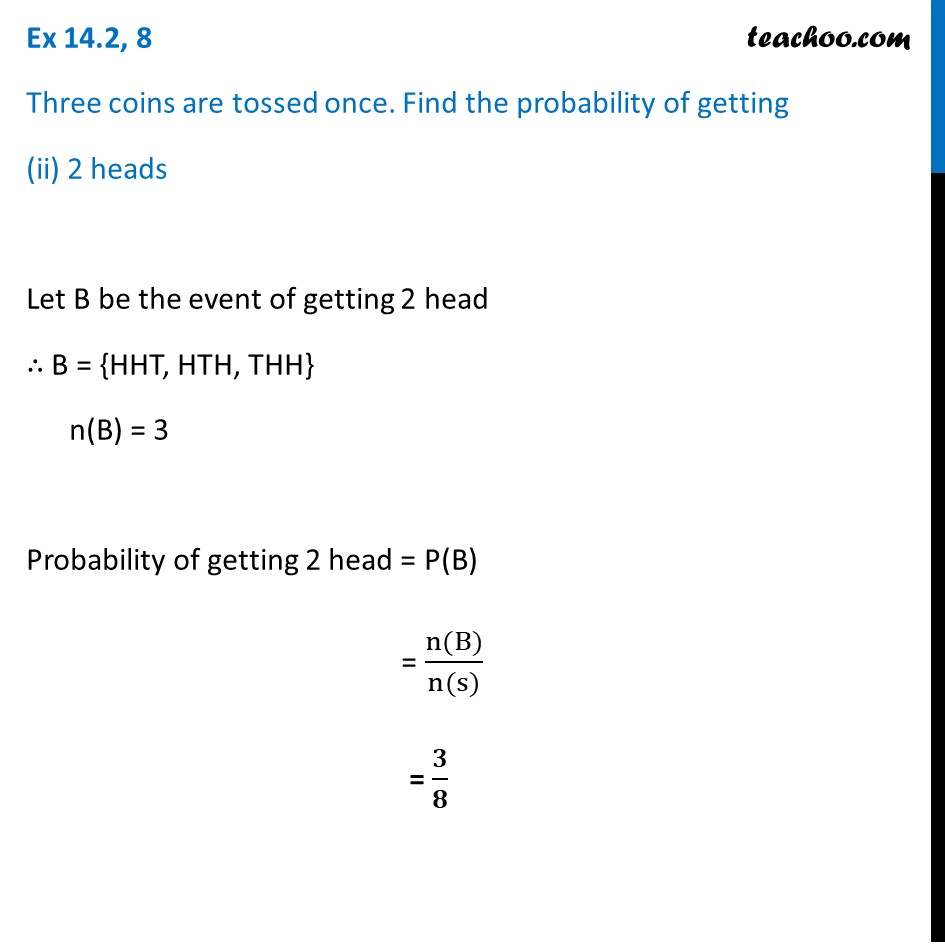
Ex 14.2, 8 Three coins are tossed once. Find the probability of getting 3 heads If 3 coins are tossed various combination possible are S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} n(S) = 23= 8 Let A be the event of getting 3 head A = {HHH} ∴ n(A) = 1 Probability of 3 heads = P(A) = (n(A))/(n(S)) = 𝟏/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (ii) 2 heads Let B be the event of getting 2 head ∴ B = {HHT, HTH, THH} n(B) = 3 Probability of getting 2 head = P(B) = (n(B))/(n(s)) = 𝟑/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (iii) at least 2 heads Let C be the event of getting at least 2 heads. C = {HHH, HHT, HTH, THH} n(C) = 4 Probability of getting at least 2 heads = P(C) = (n(C))/(n(s)) = 4/8 = 𝟏/𝟐 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (iv) at most 2 heads Let D be the event of getting at most 2 heads. i.e. getting 0 head, 1 head or 2 head D = {HHT, HTH, THH, HTT, THT, TTH, TTT} So, n(D) = 7 Probability of getting at most 2 heads = P(D) = (n(D))/(n(s)) = 𝟕/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (v) no head No head means all tails are obtained Let E be the event of getting no head So, E = {TTT} n(E) = 1 Probability of getting no head = P(E) = (n(E))/(n(s)) = 𝟏/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (vi) 3 tails Let F be the event of getting 3 tails. F = {TTT} n(F) = 1 Probability of getting 3 tails = P(F) = (n(F))/(n(s)) = 𝟏/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (vii) exactly two tails Let G be the event of getting exactly 2 tails G = {HTT, THT, TTH} n(G) = 3 Probability of getting exactly two tails = P(G) = (n(G))/(n(s)) = 𝟑/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (viii) no tail Let H be the event of getting no tail H = {HHH} n(H) = 1 Probability of getting no tails = P(H) = (n(H))/(n(s)) = 𝟏/𝟖 Ex 14.2, 8 Three coins are tossed once. Find the probability of getting (ix) at most two tails. Let I be the event of getting at most 2 tails. i.e. getting 0 tails, 1 tail or 2 tail I = {HHH, HHT, HTH, THH, HTT, THT, TTH} n(I) = 7 Probability of getting at most two tails = P(I) = (n(I))/(n(s)) = 𝟕/𝟖