RHS Congruency (Measuring Two Sides in a Right Triangle)

Transcript

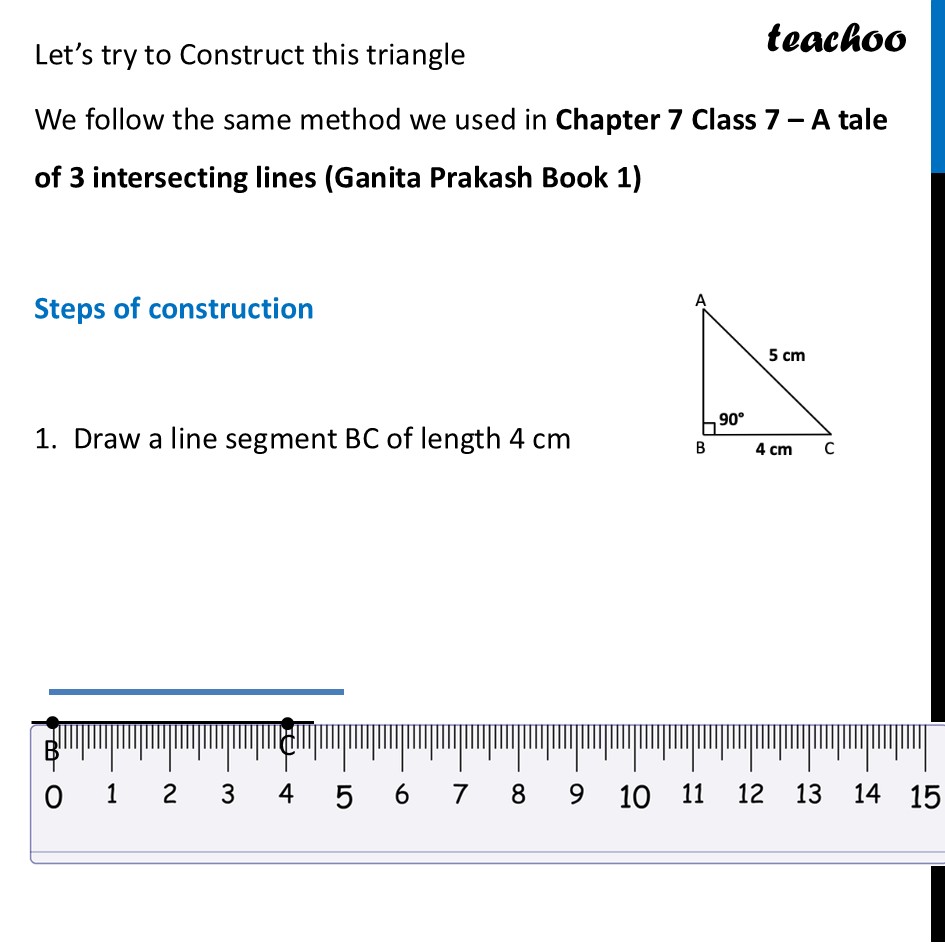
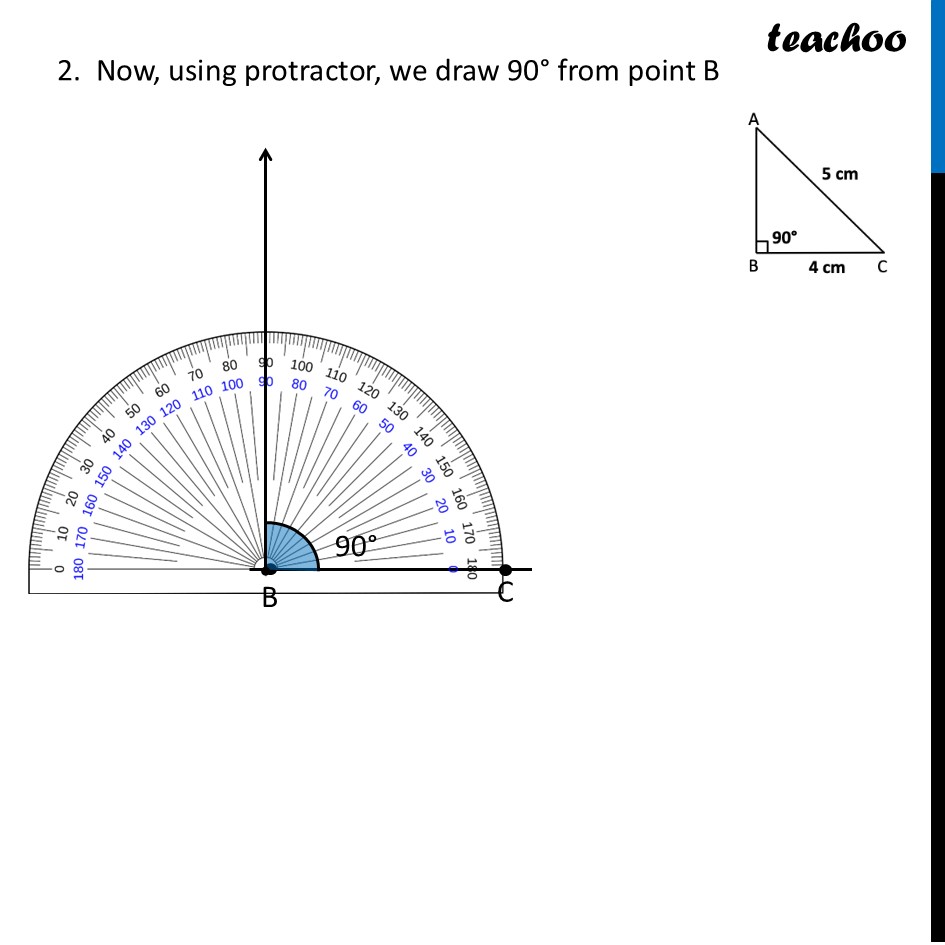
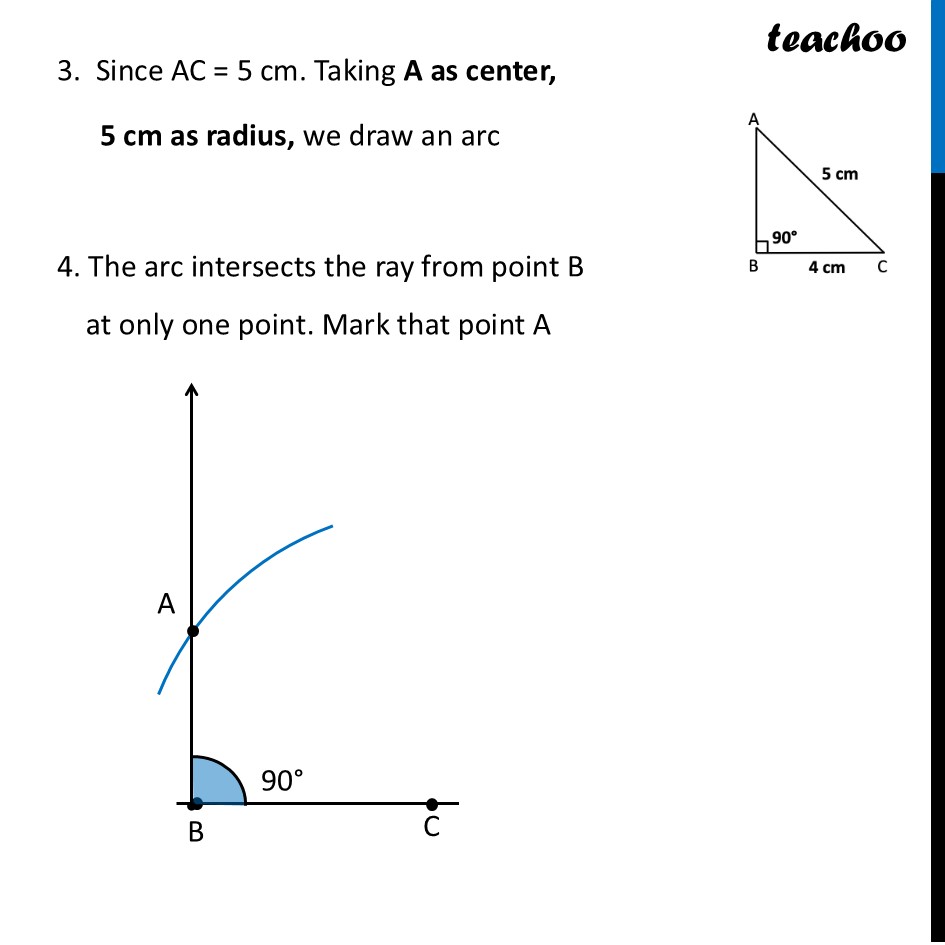
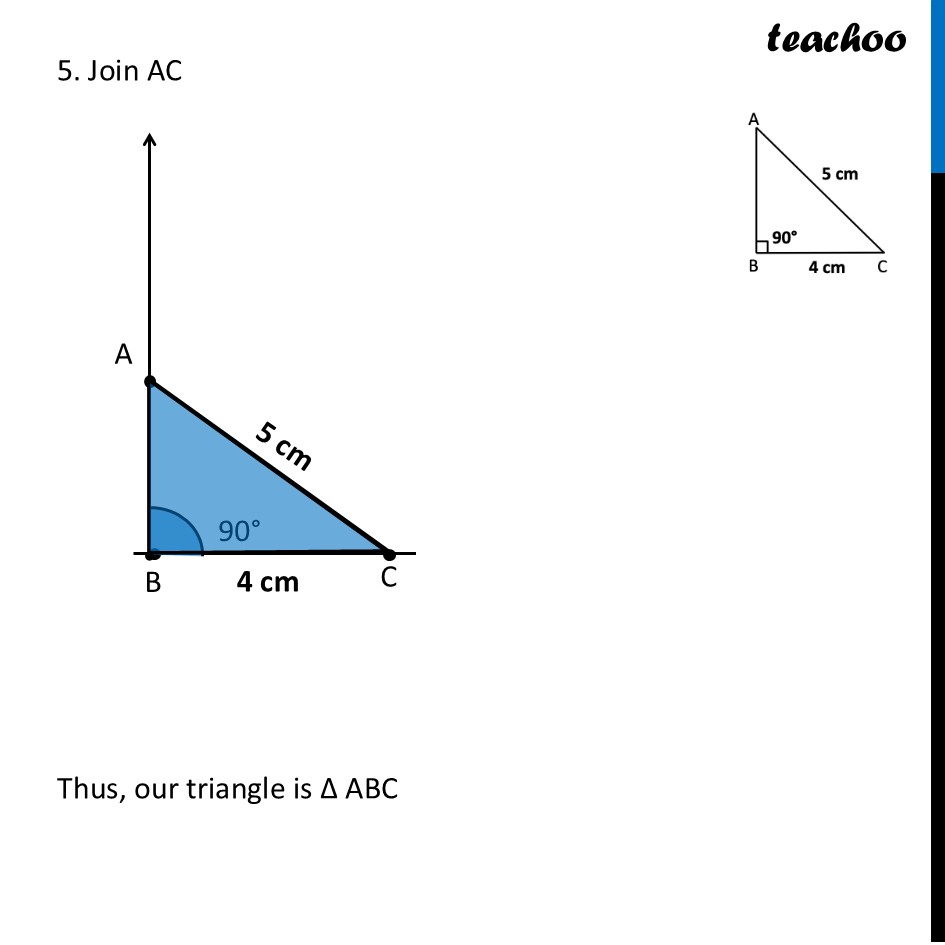
RHS Congruency (Measuring Two Sides in a Right Triangle)We saw that SSA condition doesn’t guarantee congruency. But, there is a special case where SSA guarantees congruence. That is the RHS Congruence condition. Our situation is now - ∆ABC and ∆XYZ are right-angled triangles such that BC = YZ = 4 cm, ∠B = ∠Y = 90° and AC = XZ = 5cm. Are they congruent? Let’s draw the diagram Let’s try to Construct this triangle We follow the same method we used in Chapter 7 Class 7 – A tale of 3 intersecting lines (Ganita Prakash Book 1) Steps of construction 1. Draw a line segment BC of length 4 cm 2. Now, using protractor, we draw 90° from point B 3. Since AC = 5 cm. Taking A as center, 5 cm as radius, we draw an arc 4. The arc intersects the ray from point B at only one point. Mark that point A 5. Join AC Thus, our triangle is ∆ ABC We notice that from these measurements We can create only one type of triangle. So, all triangles with these measurements are congruent Now, this is called the RHS (Right Hypotenuse Side) Congruence rule. Because both triangles have Right angle equal Hypotenuse equal One side equal Thus, we can conclude When right angle, hypotenuse and another side (RHS) of two triangles are equal, the two triangles are congruent.