Question 4 - Figure it out - Page 14 - Chapter 1 Class 7 - Geometric Twins (Ganita Prakash II)

Transcript

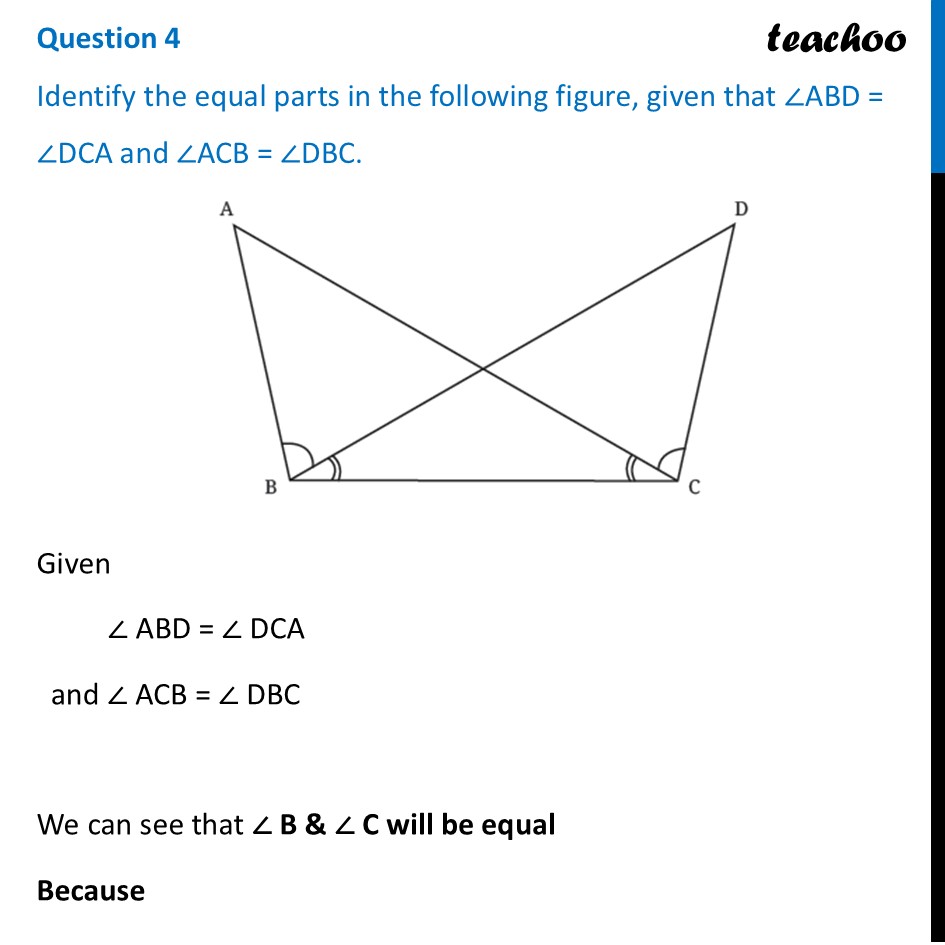
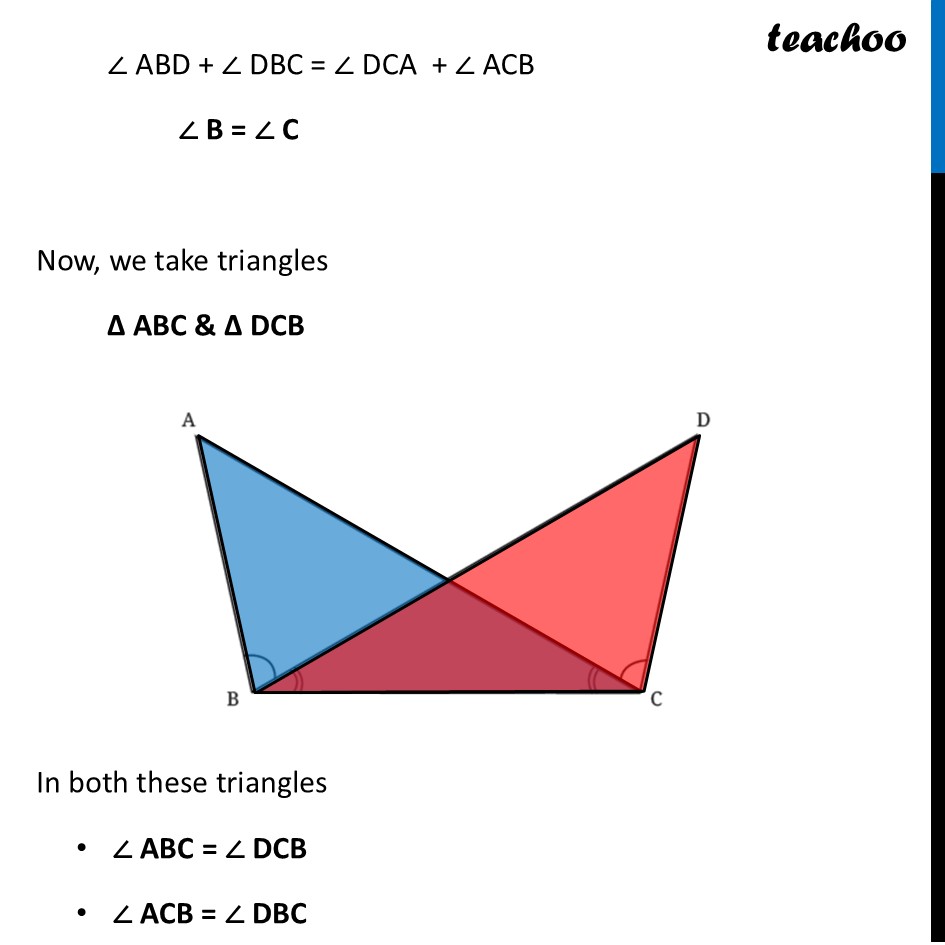
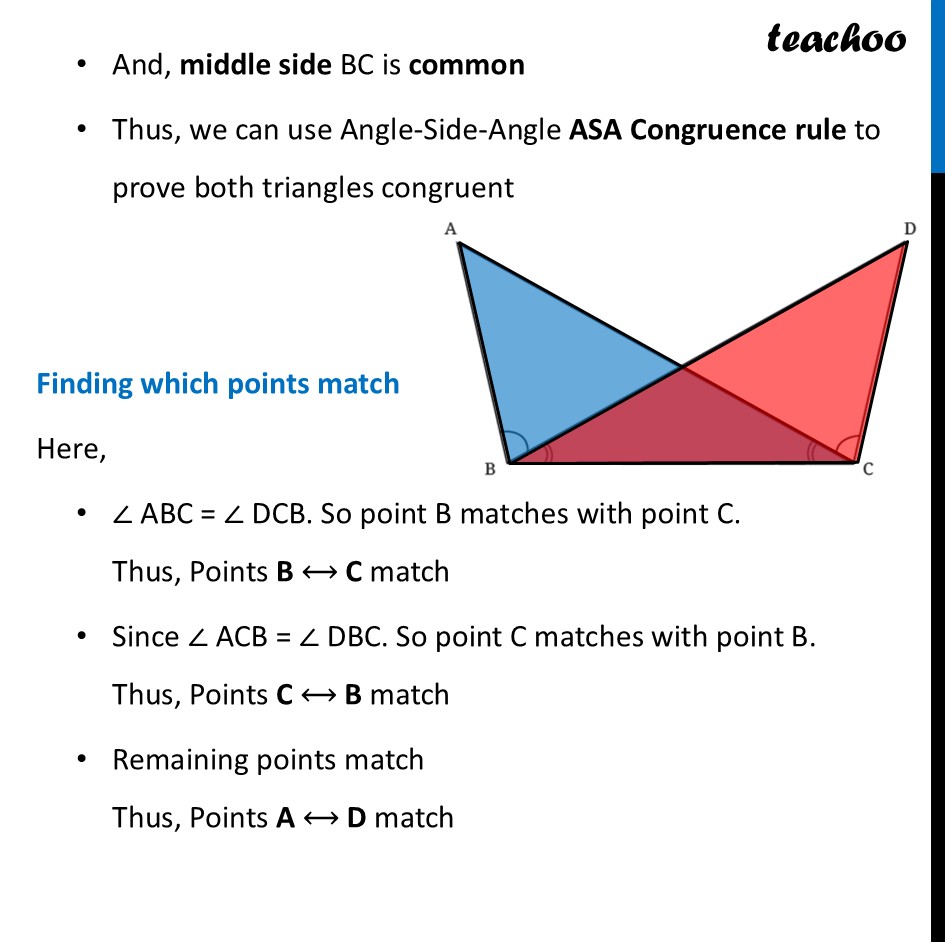
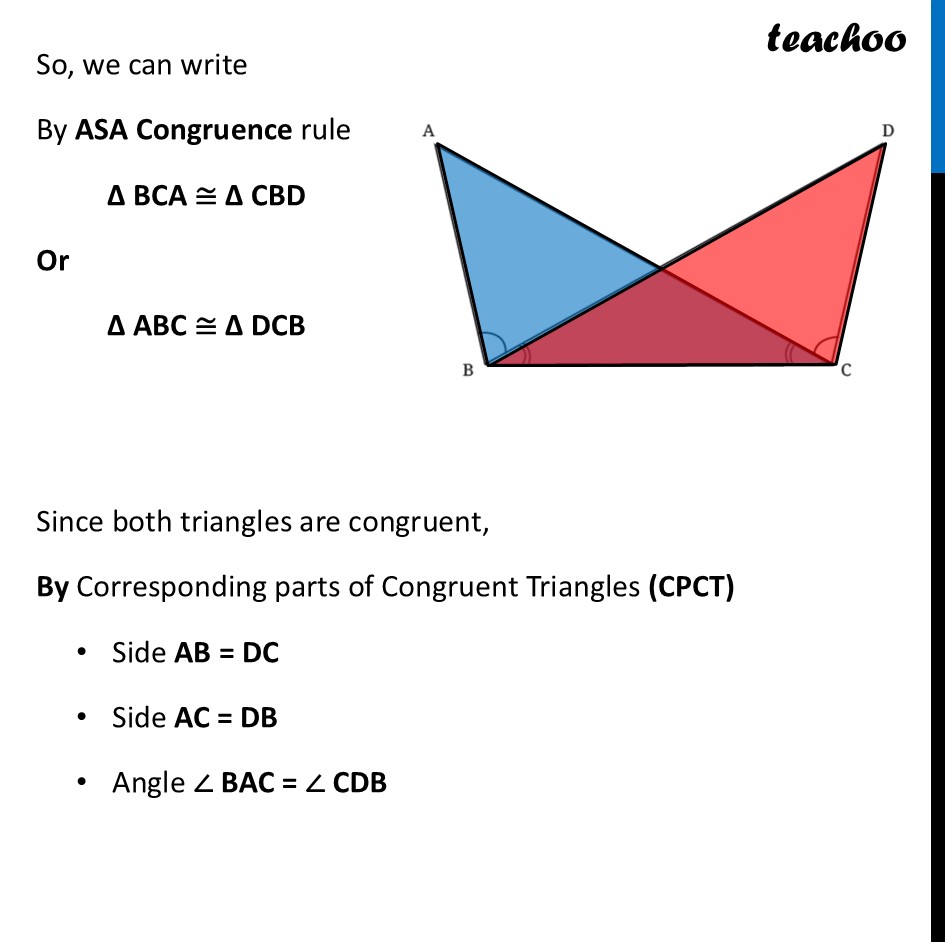
Question 4 Identify the equal parts in the following figure, given that ∠ABD = ∠DCA and ∠ACB = ∠DBC.Given ∠ ABD = ∠ DCA and ∠ ACB = ∠ DBC We can see that ∠ B & ∠ C will be equal Because ∠ ABD + ∠ DBC = ∠ DCA + ∠ ACB ∠ B = ∠ C Now, we take triangles ∆ ABC & ∆ DCB In both these triangles ∠ ABC = ∠ DCB ∠ ACB = ∠ DBC And, middle side BC is common Thus, we can use Angle-Side-Angle ASA Congruence rule to prove both triangles congruent Finding which points match Here, ∠ ABC = ∠ DCB. So point B matches with point C. Thus, Points B ⟷ C match Since ∠ ACB = ∠ DBC. So point C matches with point B. Thus, Points C ⟷ B match Remaining points match Thus, Points A ⟷ D match So, we can write By ASA Congruence rule ∆ BCA ≅ ∆ CBD Or ∆ ABC ≅ ∆ DCB Since both triangles are congruent, By Corresponding parts of Congruent Triangles (CPCT) Side AB = DC Side AC = DB Angle ∠ BAC = ∠ CDB