Question 3 - Figure it out - Page 14 - Chapter 1 Class 7 - Geometric Twins (Ganita Prakash II)

Transcript

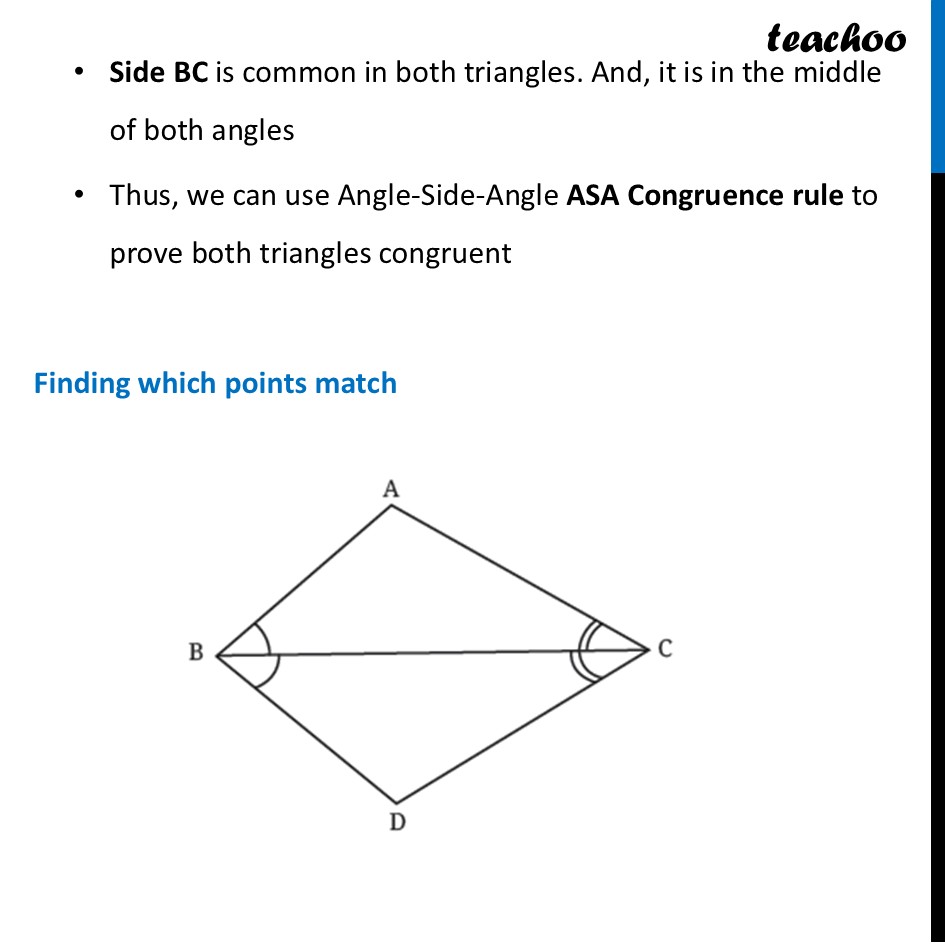
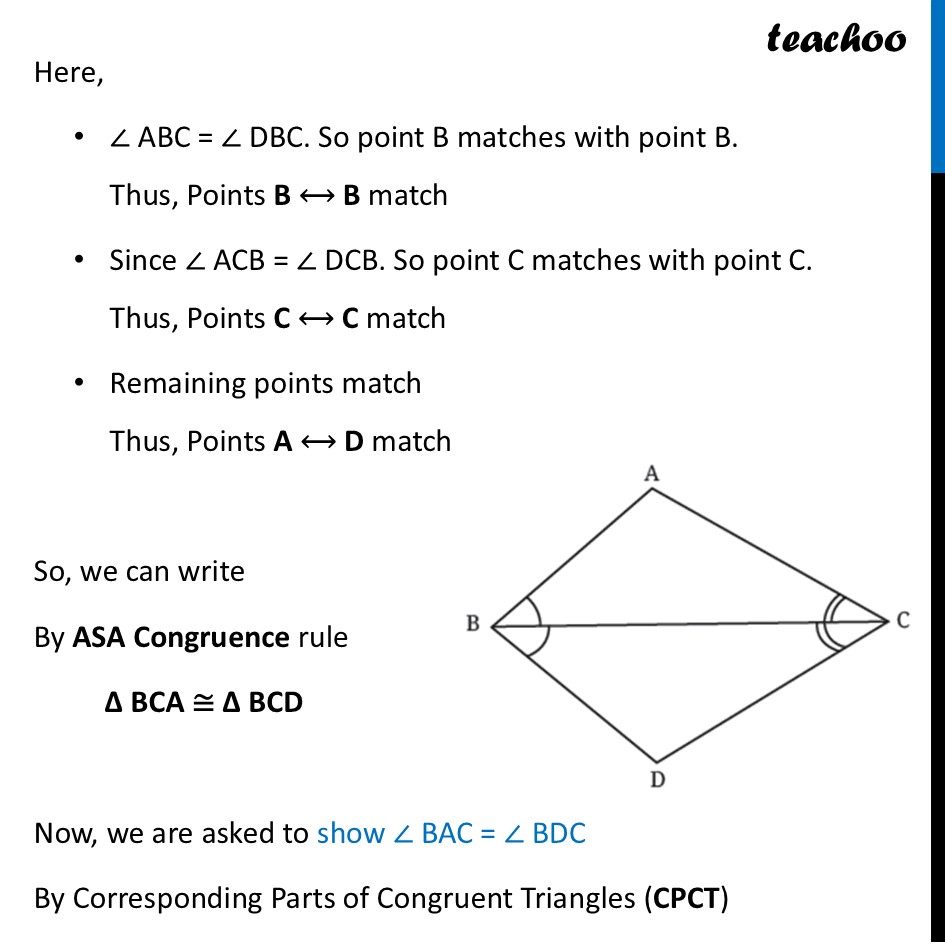
Question 3 Given that ∠ABC = ∠DBC and ∠ACB = ∠DCB, show that ∠BAC = ∠BDC. Are the two triangles congruent?To prove the third angle equal in both triangles, We first prove these triangles congruent Now, One angle is equal, ∠ ABC = ∠ DBC Another angle is equal, ∠ ACB = DCB Side BC is common in both triangles. And, it is in the middle of both angles Thus, we can use Angle-Side-Angle ASA Congruence rule to prove both triangles congruent Finding which points match Here, ∠ ABC = ∠ DBC. So point B matches with point B. Thus, Points B ⟷ B match Since ∠ ACB = ∠ DCB. So point C matches with point C. Thus, Points C ⟷ C match Remaining points match Thus, Points A ⟷ D match So, we can write By ASA Congruence rule ∆ BCA ≅ ∆ BCD Now, we are asked to show ∠ BAC = ∠ BDC By Corresponding Parts of Congruent Triangles (CPCT) Corresponding angles are equal. Therefore, ∠ BAC = ∠ BDC Hence proved