Question 2 - Figure it out - Page 14 - Chapter 1 Class 7 - Geometric Twins (Ganita Prakash II)

Transcript

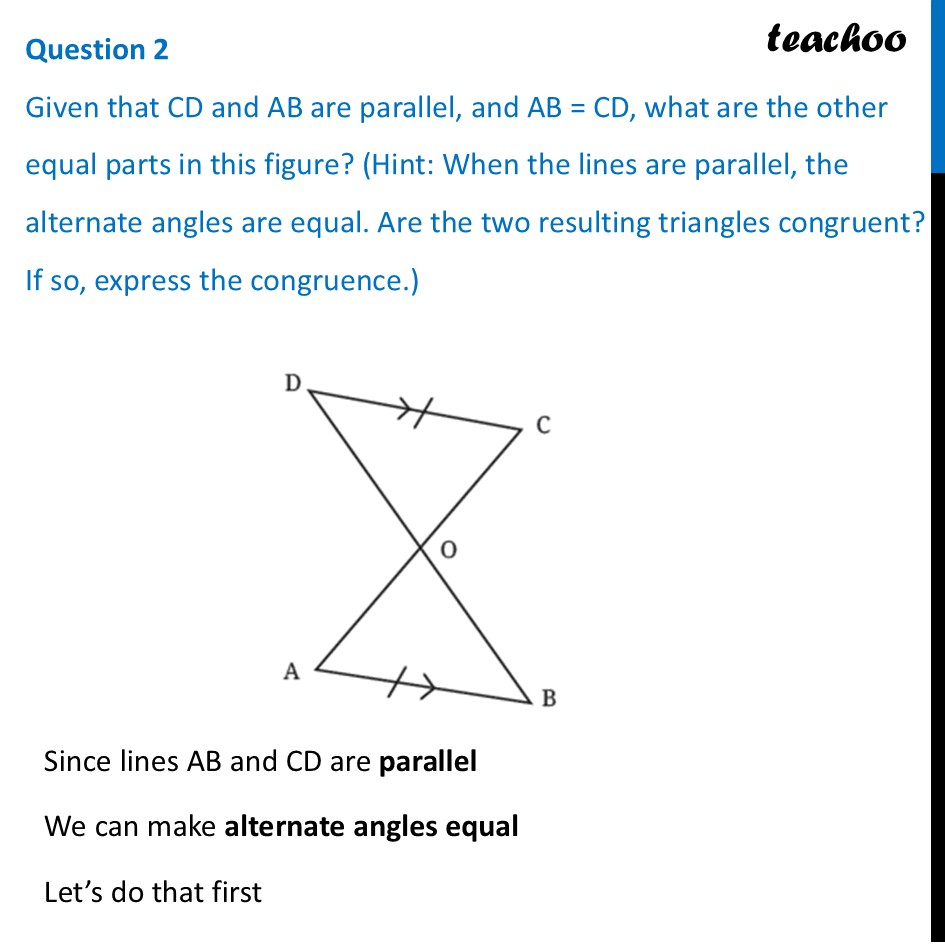
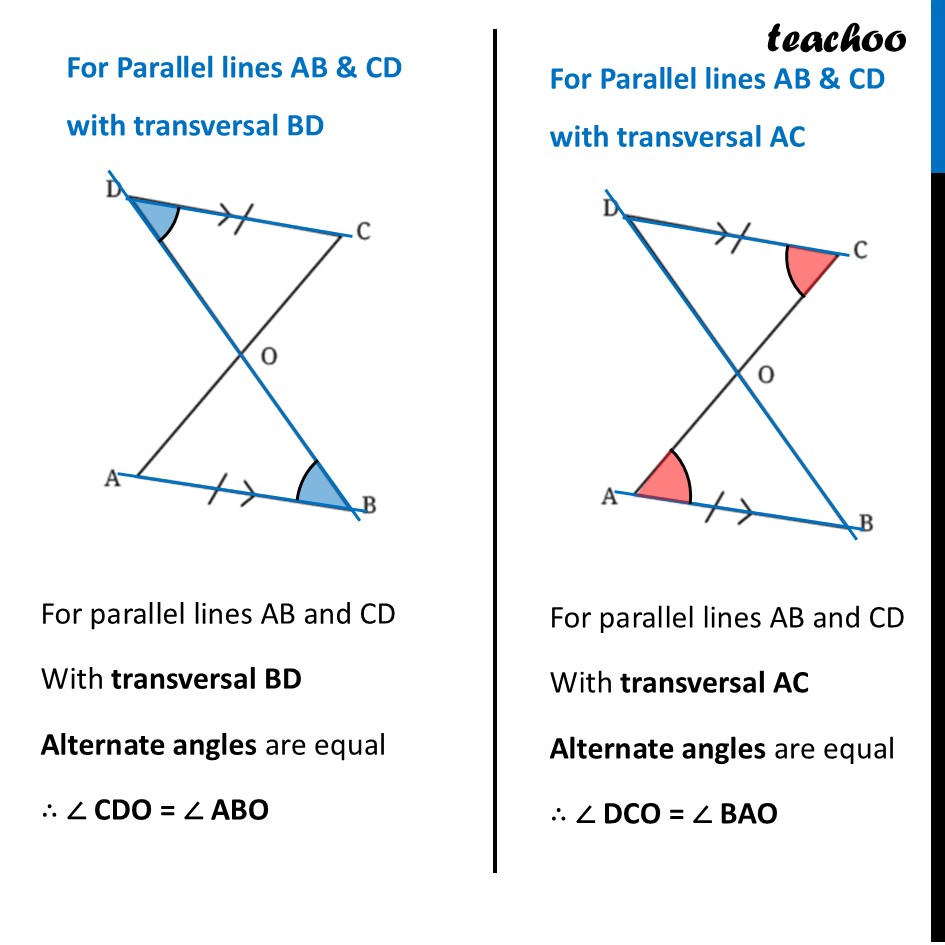
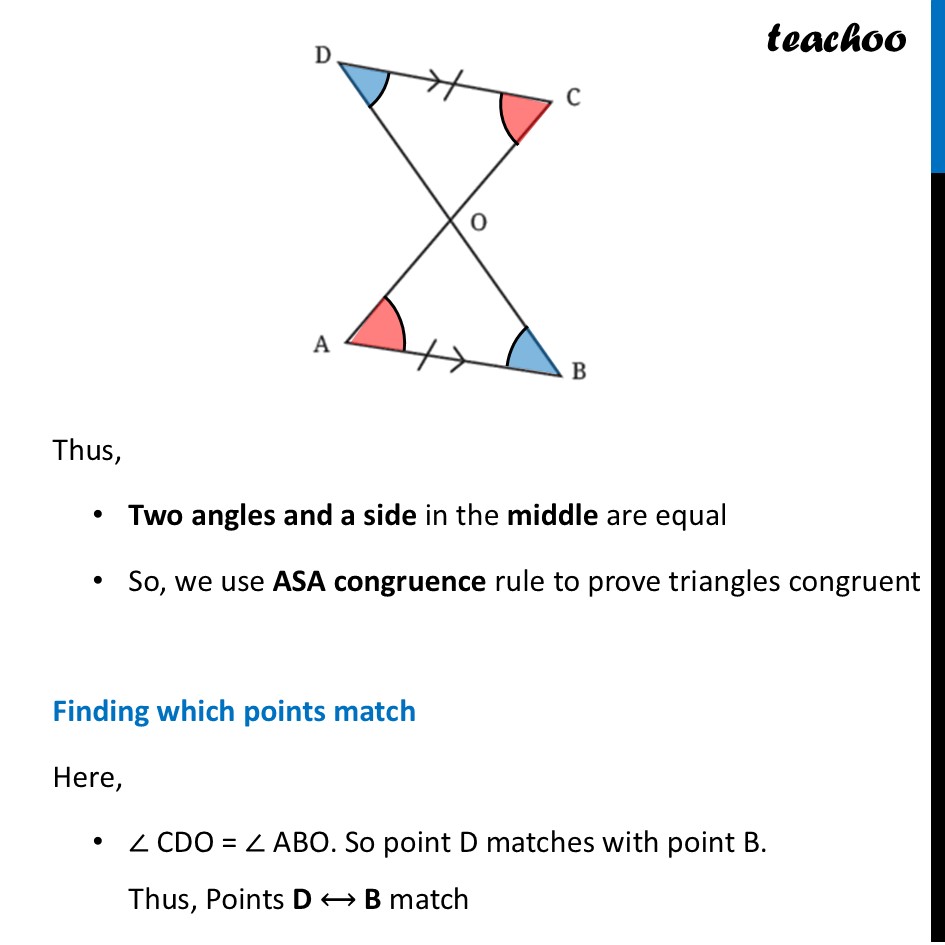
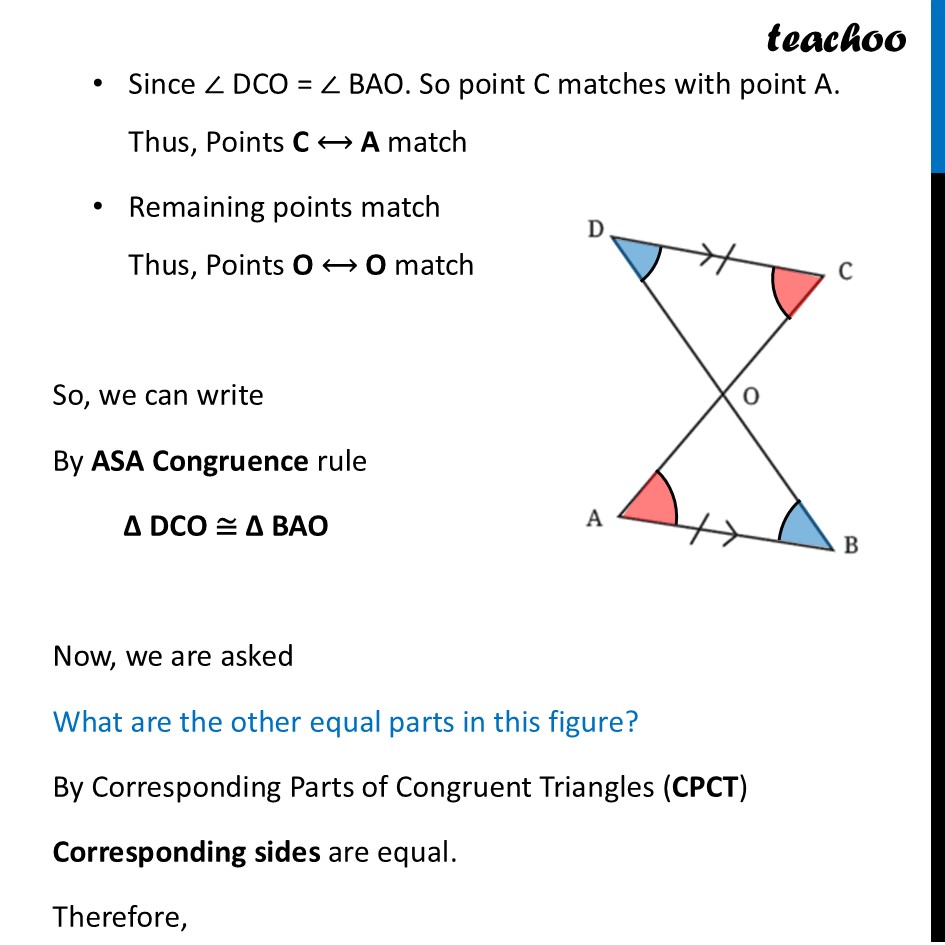
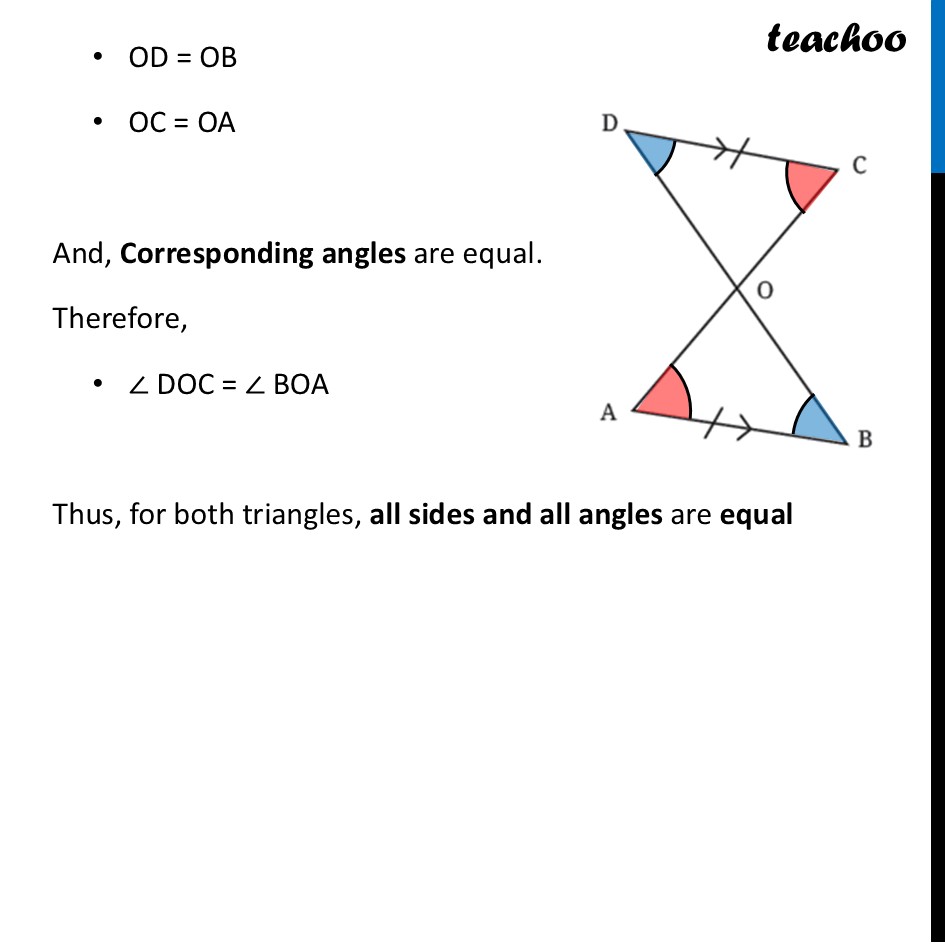
Question 2 Given that CD and AB are parallel, and AB = CD, what are the other equal parts in this figure? (Hint: When the lines are parallel, the alternate angles are equal. Are the two resulting triangles congruent? If so, express the congruence.)Since lines AB and CD are parallel We can make alternate angles equal Let’s do that first For Parallel lines AB & CD with transversal BDFor parallel lines AB and CD With transversal BD Alternate angles are equal ∴ ∠ CDO = ∠ ABO For Parallel lines AB & CD with transversal AC For parallel lines AB and CD With transversal AC Alternate angles are equal ∴ ∠ DCO = ∠ BAO Thus, Two angles and a side in the middle are equal So, we use ASA congruence rule to prove triangles congruent Finding which points match Here, ∠ CDO = ∠ ABO. So point D matches with point B. Thus, Points D ⟷ B match Since ∠ DCO = ∠ BAO. So point C matches with point A. Thus, Points C ⟷ A match Remaining points match Thus, Points O ⟷ O match So, we can write By ASA Congruence rule ∆ DCO ≅ ∆ BAO Now, we are asked What are the other equal parts in this figure? By Corresponding Parts of Congruent Triangles (CPCT) Corresponding sides are equal. Therefore, OD = OB OC = OA And, Corresponding angles are equal. Therefore, ∠ DOC = ∠ BOA Thus, for both triangles, all sides and all angles are equal