Power Line of 7

Transcript

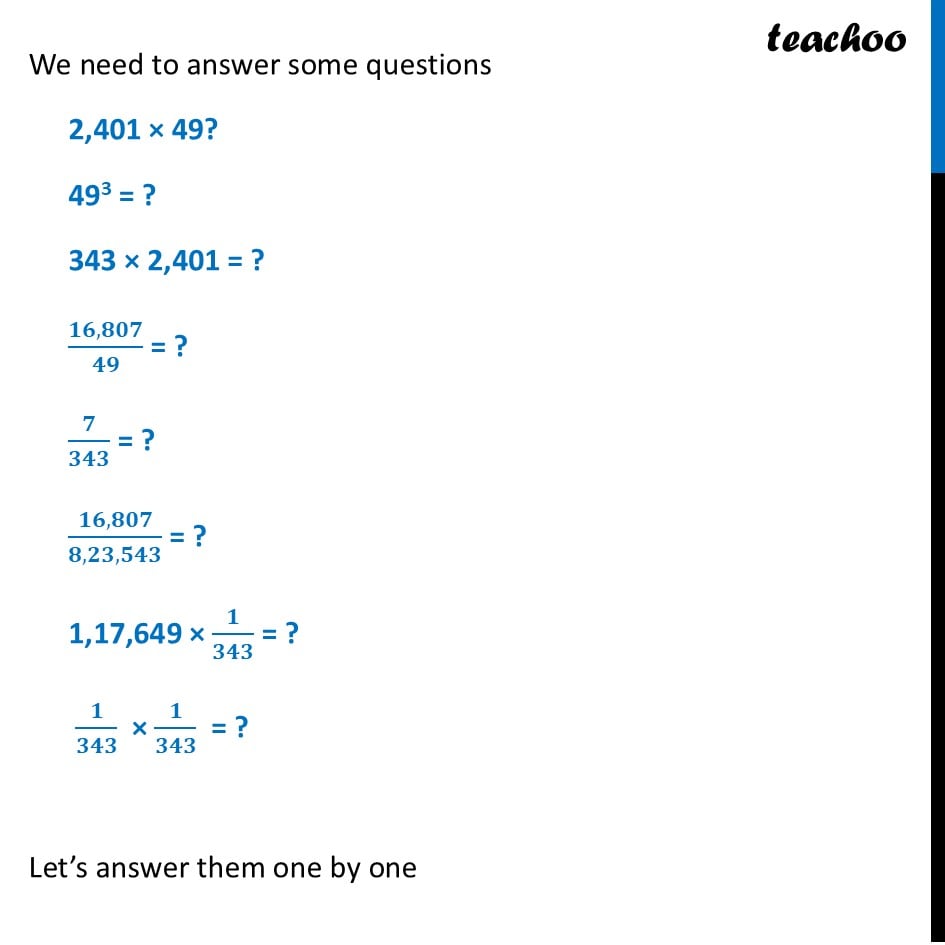
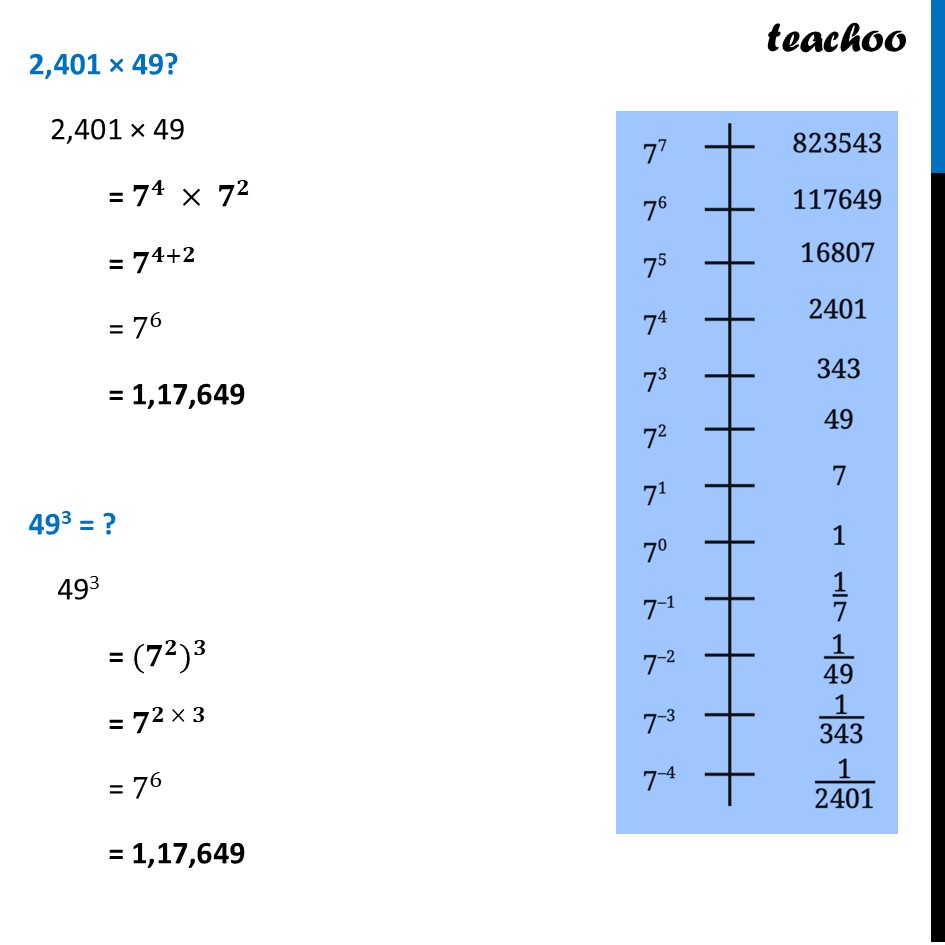
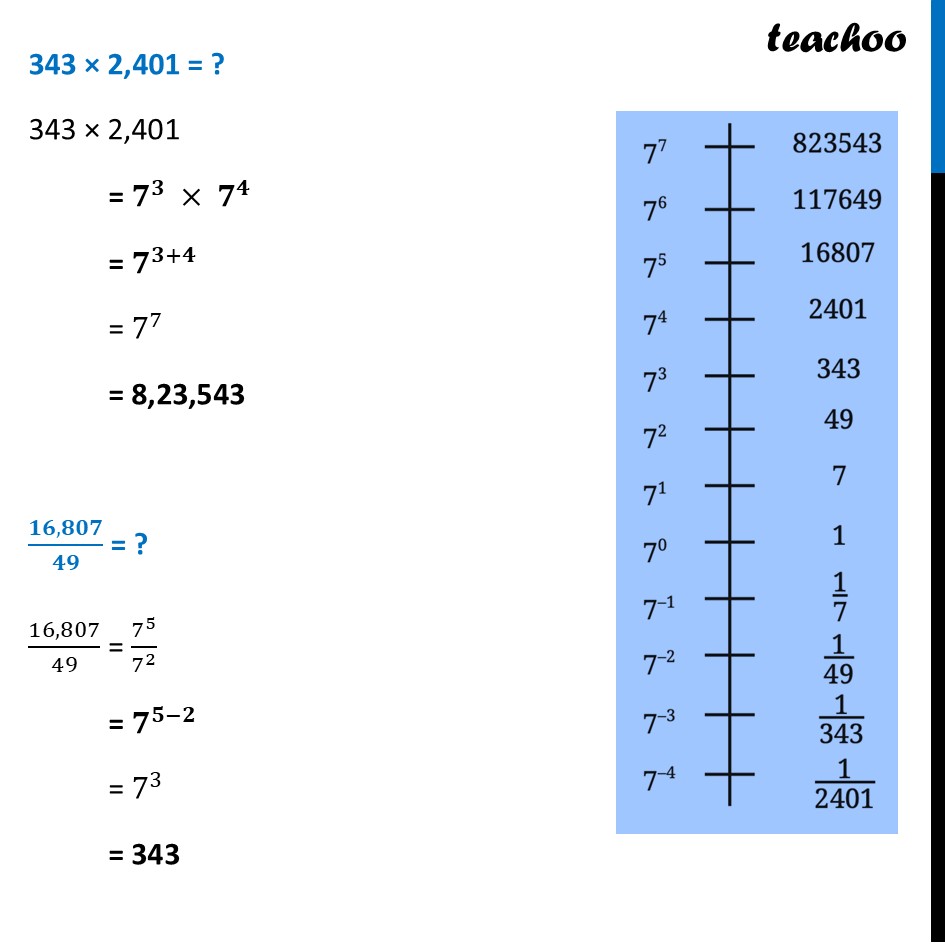
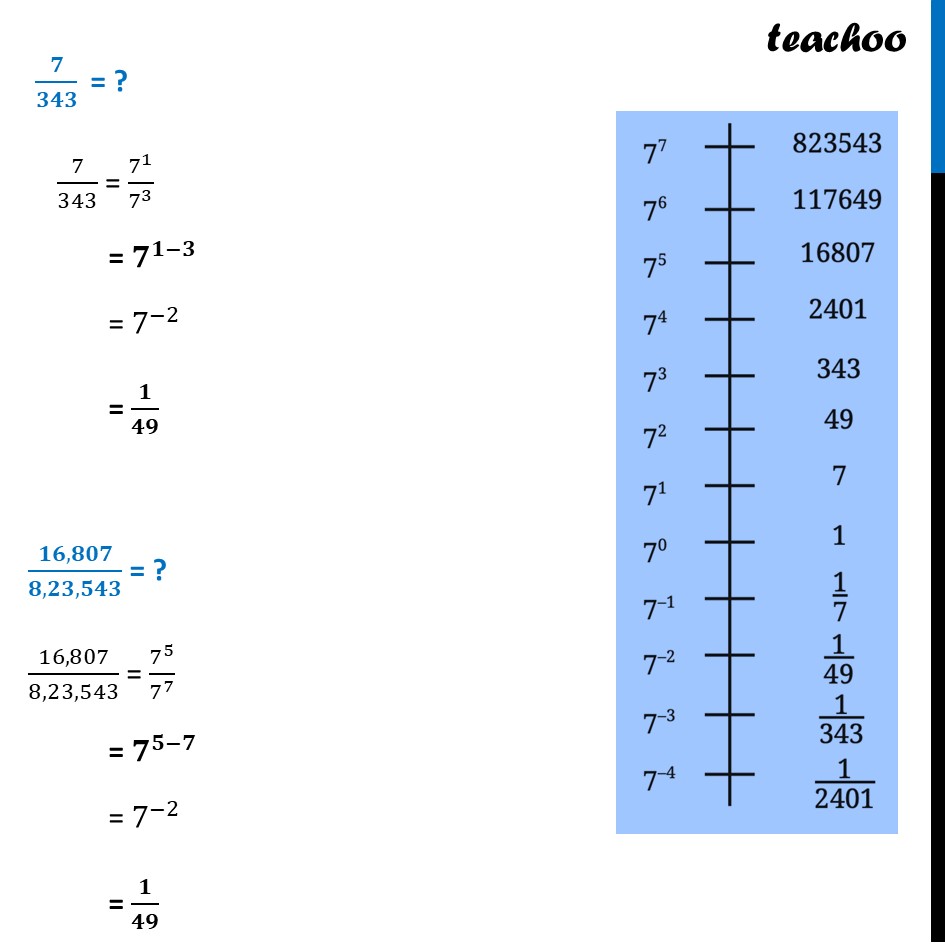
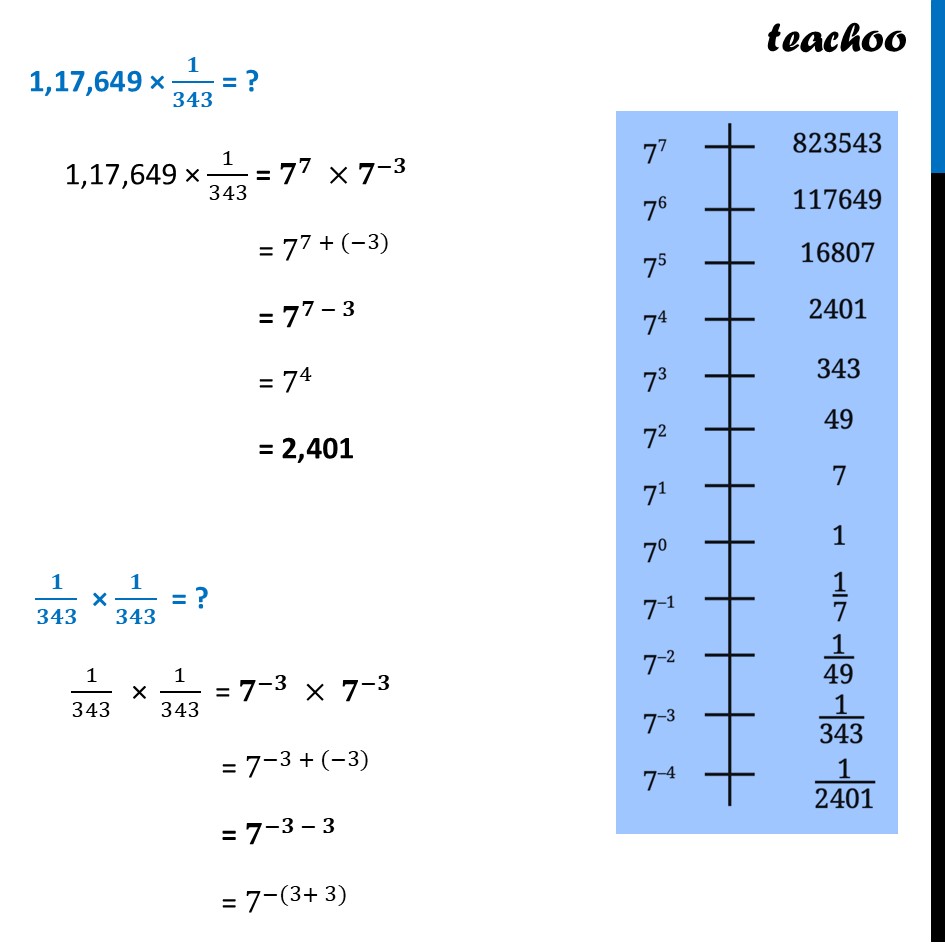
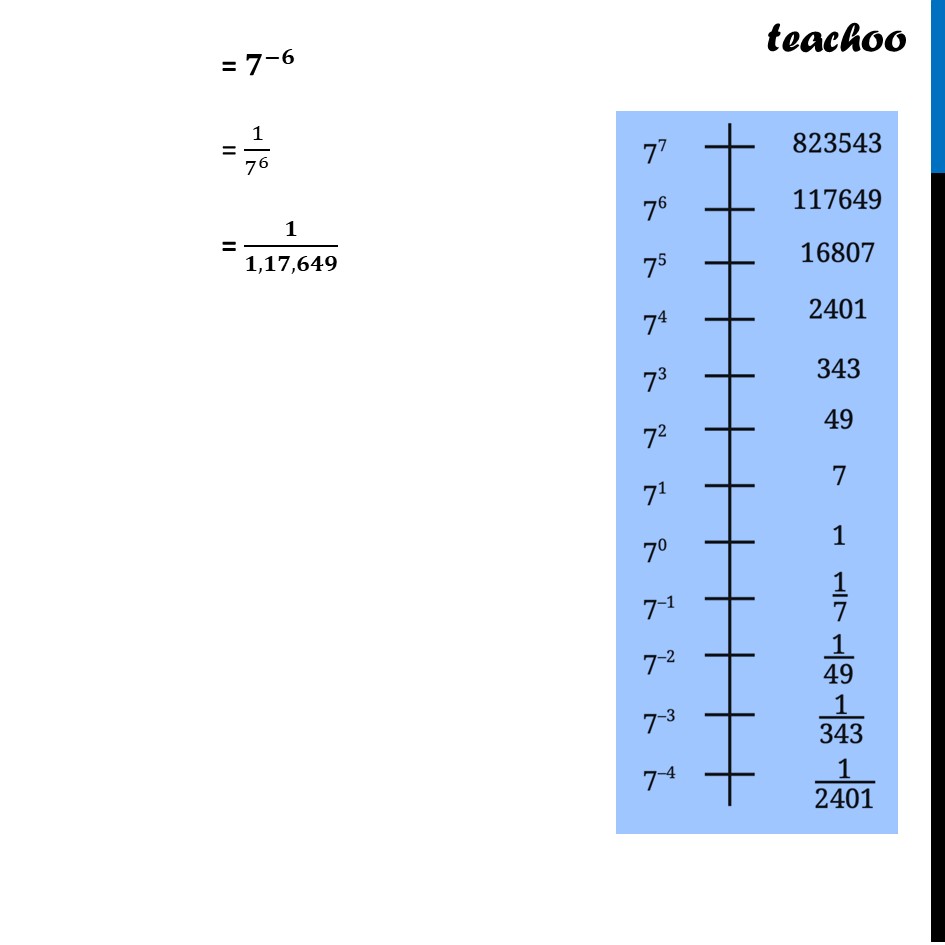
Power Line of 7Power line of 7 looks like Power is decreasing as we go down ■(7^7&-&823543@7^6&-&117649@7^5&-&16807@7^4&-&2401@7^3&-&343@7^2&-&49@7^1&-&7@7^0&-&1@7^(-1)&-&1/7@7^(-2)&-&1/49@7^(-3)&-&1/343@7^(-4)&-&1/2401)We need to answer some questions 2,401 × 49? 493 = ? 343 × 2,401 = ? (𝟏𝟔,𝟖𝟎𝟕)/𝟒𝟗 = ? 𝟕/𝟑𝟒𝟑 = ? (𝟏𝟔,𝟖𝟎𝟕)/(𝟖,𝟐𝟑,𝟓𝟒𝟑) = ? 1,17,649 × 𝟏/𝟑𝟒𝟑 = ? 𝟏/𝟑𝟒𝟑 × 𝟏/𝟑𝟒𝟑 = ? Let’s answer them one by one 2,401 × 49? 2,401 × 49 = 𝟕^𝟒 × 𝟕^𝟐 = 𝟕^(𝟒+𝟐) = 7^6 = 1,17,649 493 = ? 493 = 〖(𝟕^𝟐)〗^𝟑 = 𝟕^(𝟐 × 𝟑) = 7^6 = 1,17,649 𝟕/𝟑𝟒𝟑 " = ?" 7/343 = 7^1/7^3 = 𝟕^(𝟏−𝟑) = 7^(−2) = 𝟏/𝟒𝟗 (𝟏𝟔,𝟖𝟎𝟕)/(𝟖,𝟐𝟑,𝟓𝟒𝟑) = ? 16,807/8,23,543 = 7^5/7^7 = 𝟕^(𝟓−𝟕) = 7^(−2) = 𝟏/𝟒𝟗 343 × 2,401 = ? 343 × 2,401 = 𝟕^𝟑 × 𝟕^𝟒 = 𝟕^(𝟑+𝟒) = 7^7 = 8,23,543 (𝟏𝟔,𝟖𝟎𝟕)/𝟒𝟗 = ? 16,807/49 = 7^5/7^2 = 𝟕^(𝟓−𝟐) = 7^3 = 343 1,17,649 × 𝟏/𝟑𝟒𝟑 = ? 1,17,649 × 1/343 = 𝟕^𝟕 ×𝟕^(−𝟑) = 7^(7 + (−3)) = 𝟕^(𝟕 − 𝟑) = 7^4 = 2,401 𝟏/𝟑𝟒𝟑 × 𝟏/𝟑𝟒𝟑 = ? 1/343 " × " 1/343 = 𝟕^(−𝟑) × 𝟕^(−𝟑) = 7^(−3 + (−3)) = 𝟕^(−𝟑 − 𝟑) = 7^(−(3+ 3)) = 𝟕^(−𝟔) = 1/7^6 = 𝟏/(𝟏,𝟏𝟕,𝟔𝟒𝟗)