Successive Differences

Transcript

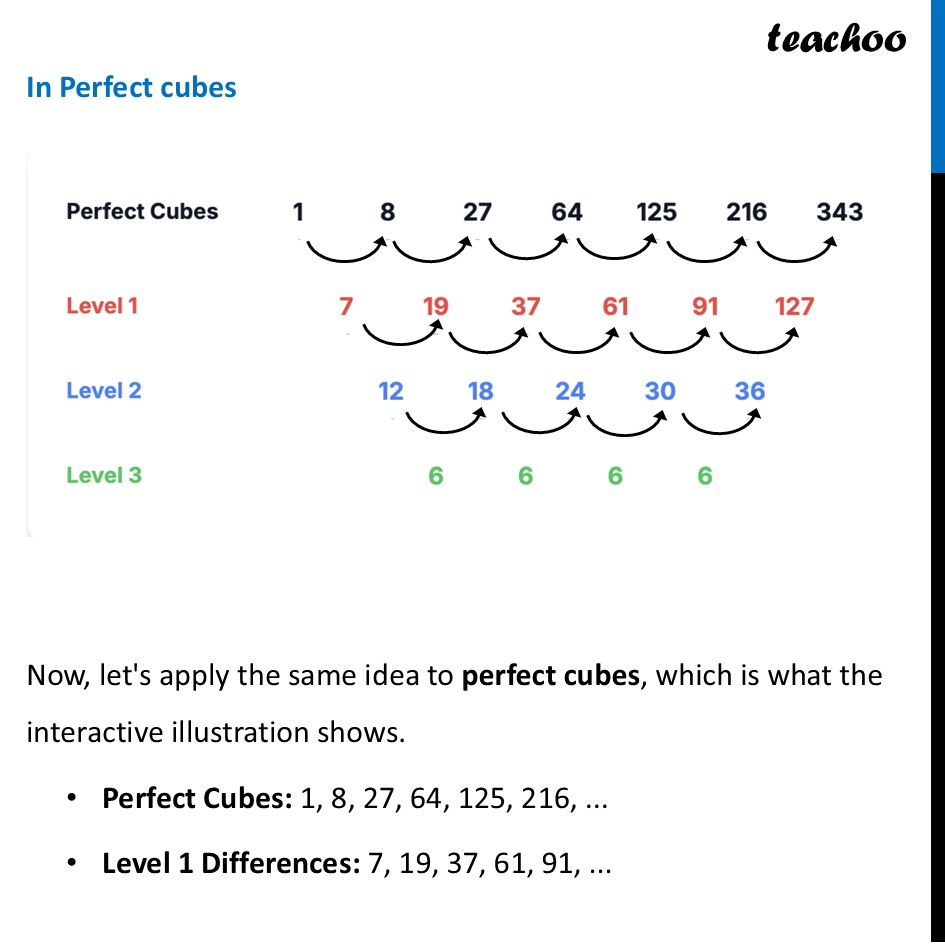
Successive Differences Let’s look at the pattern in Perfect Squares If you start with the sequence of perfect squares and calculate the differences between consecutive numbers, you get a new sequence (Level 1). Perfect Squares: 1, 4, 9, 16, 25, ... Level 1 Differences: 3, 5, 7, 9, ... (the odd numbers) If you do it again for that new sequence, you find something remarkable: Level 2 Differences: 2, 2, 2, 2, ... The differences become a constant number (2) at the second level. Now, let’s look at Perfect cubes In Perfect cubes Now, let's apply the same idea to perfect cubes, which is what the interactive illustration shows. Perfect Cubes: 1, 8, 27, 64, 125, 216, ... Level 1 Differences: 7, 19, 37, 61, 91, ... Now, let's apply the same idea to perfect cubes, which is what the interactive illustration shows. Perfect Cubes: 1, 8, 27, 64, 125, 216, ... Level 1 Differences: 7, 19, 37, 61, 91, ... Level 2 Differences: 12, 18, 24, 30, ... At this point, the numbers are not constant, but you might notice they are all multiples of 6. If we go one level deeper, the magic happens: Level 3 Differences: 6, 6, 6, 6, ... For perfect cubes, the differences become a constant number (6) at the third level. What does it mean? This isn't a coincidence! It's a fundamental property of polynomial sequences. A sequence of squares is a degree-2 polynomial (n2). Its constant difference appears at Level 2. A sequence of cubes is a degree-3 polynomial (n3). Its constant difference appears at Level 3. This pattern continues! For a sequence of fourth powers (n4), you would find a constant difference at the fourth level.