Properties of Perfect Squares

Transcript

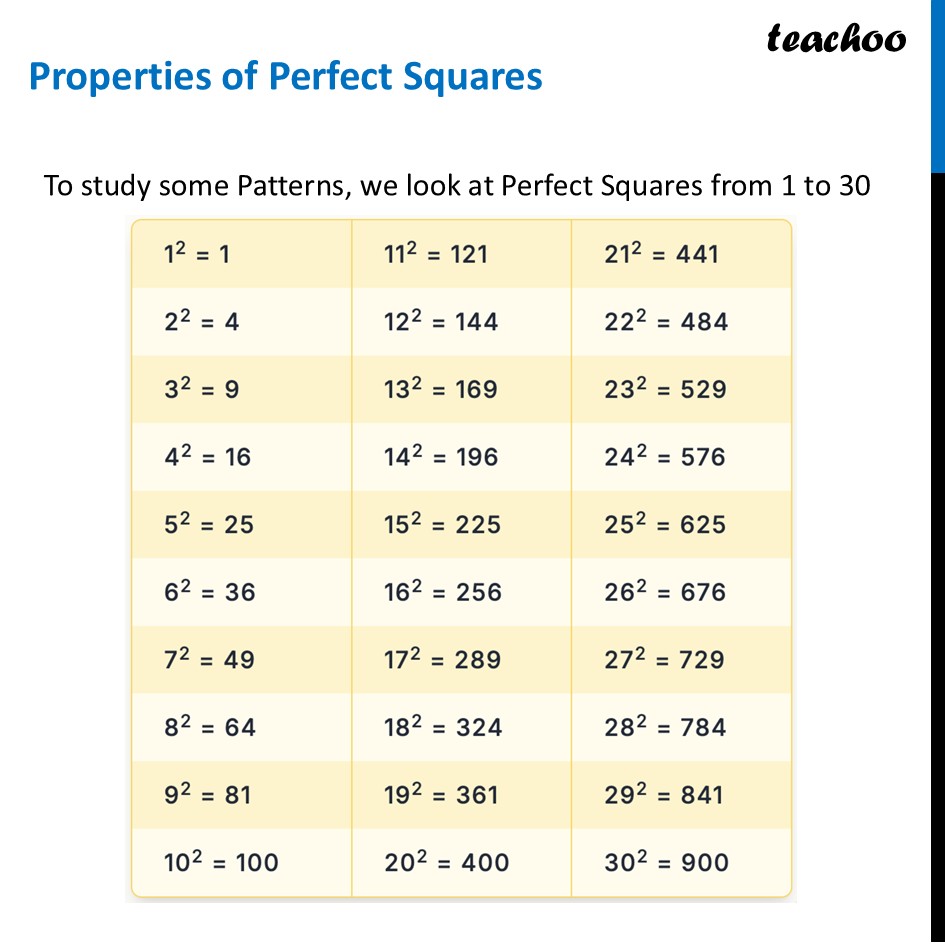
Properties of Perfect Squares To study some Patterns, we look at Perfect Squares from 1 to 30 Property 1 – Ending Digits Perfect squares can only end in the digits 0, 1, 4, 5, 6, or 9. They never end in 2, 3, 7, or 8. This is a quick way to tell if a number is not a perfect square. Example: 28, 97 are not a perfect square 1000 may be a perfect square Property 2 – If number’s last digit is 1 or 9 If a number's last digit is 1 or 9, its square will end in 1. Example: 192 = 361 212 = 441 Property 3 – If number’s last digit is 4 or 6 If a number's last digit is 4 or 6, its square will end in 6. Example: 142 = 196 562 = 3136 Property 4 – Zero’s at the end A square number can only have an even number of zeros at the end. Example: 102 = 100 (two zeros) 10002 = 1000000 (six zeros) Thus, we can say 1000 (three zeros) is not a perfect square Property 5 – Square of even and odd number Square of even numbers are always even, Square of odd numbers are always odd Example: Square of 2 is 4, Square of 6 is 36 And Square of 7 is 49 Square of 9 is 81 Property 6 – Unit digit of any square number Unit digit of square of any number will be the unit digit of its last digit For number 29 Unit digit of 292 = Unit digit of 92 = Unit digit of 81 = 1 For number 76 Unit digit of 762 = Unit digit of 62 = Unit digit of 36 = 6 Thus, we can say parity of a number (whether it is even or odd) and its square are related Property 7 – Perfect square when divided by 3 A perfect square always leaves remainder 0 or 1 when divided by 3 Example: Perfect Square numbers are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 1 on divided by 3 leaves remainder 1 4 on divided by 3 leaves remainder 1 9 on divided by 3 leaves remainder 0 16 on divided by 3 leaves remainder 1 25 on divided by 3 leaves remainder 1 Checking if 98 is a perfect square, We divide 98 by 3 It leaves remainder 2 So, it is not a perfect square