Example 4 - Page 122 - Chapter 5 Class 7 - Parallel and Intersecting Lines (Ganita Prakash)

Transcript

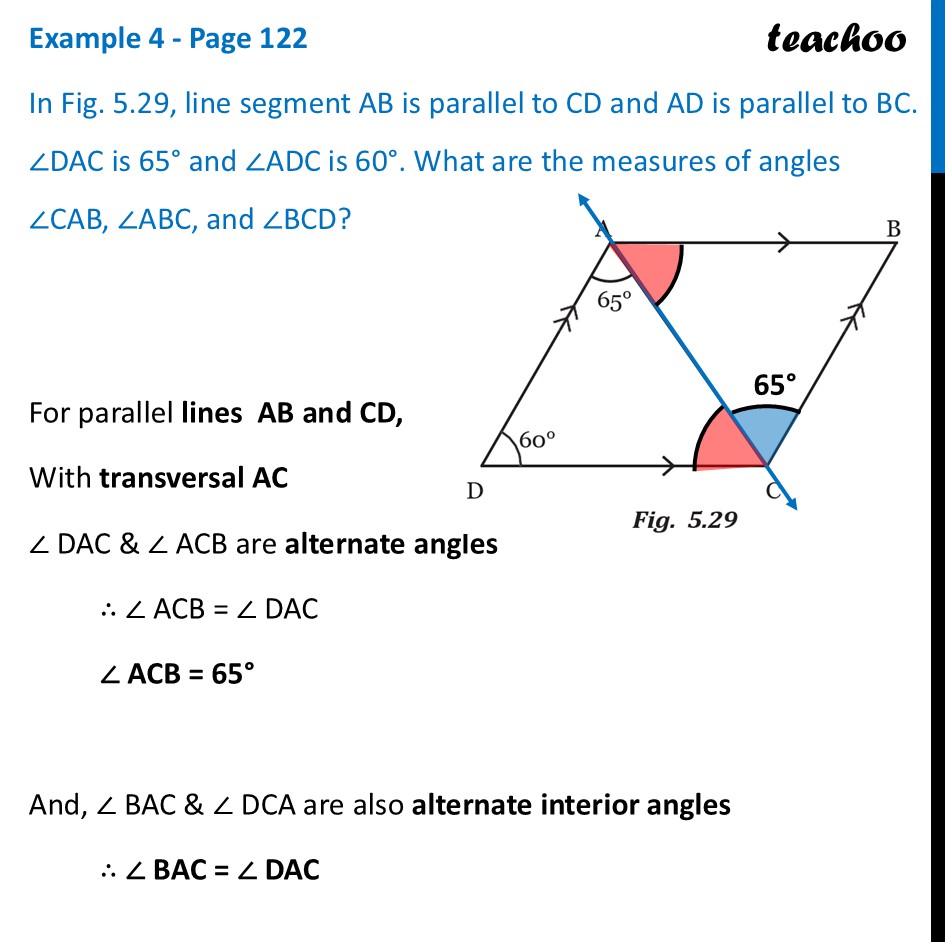
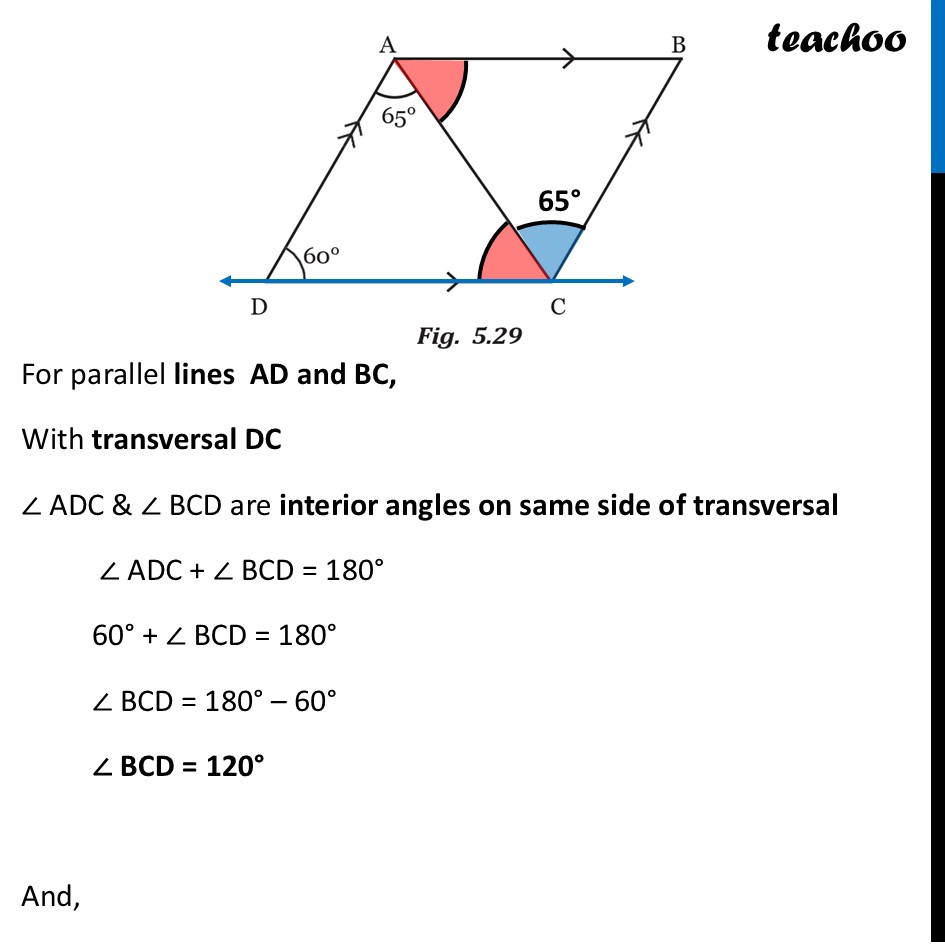
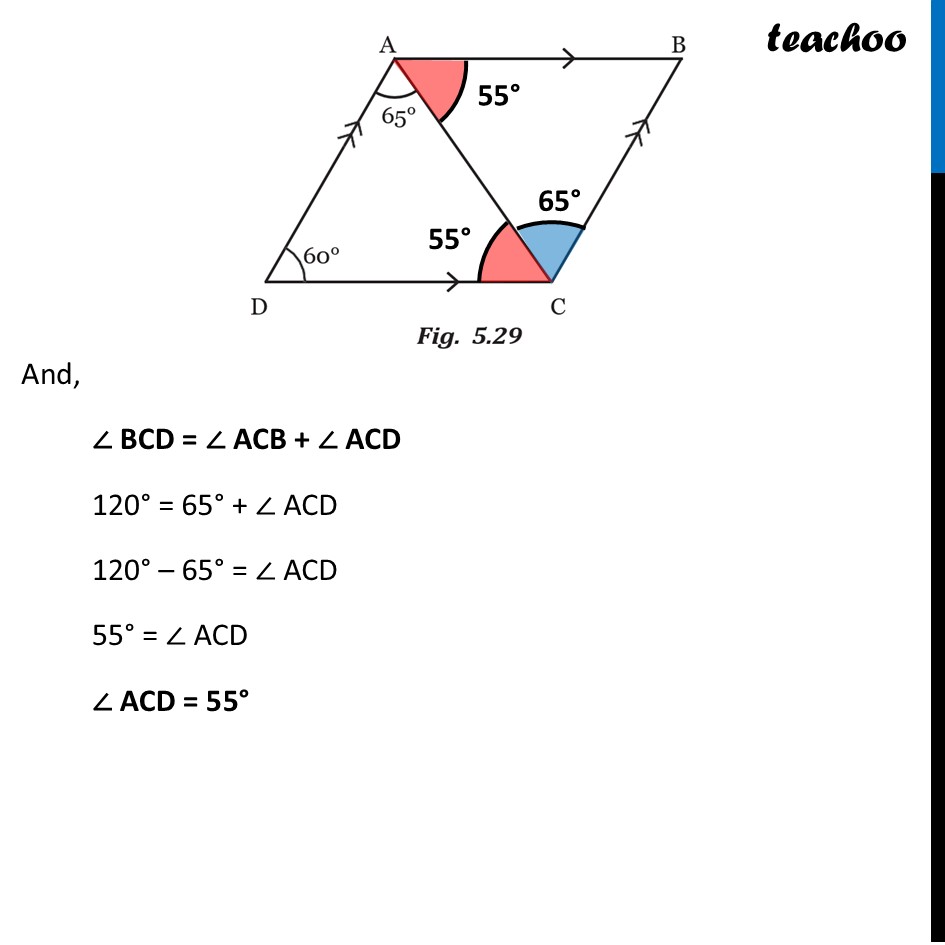
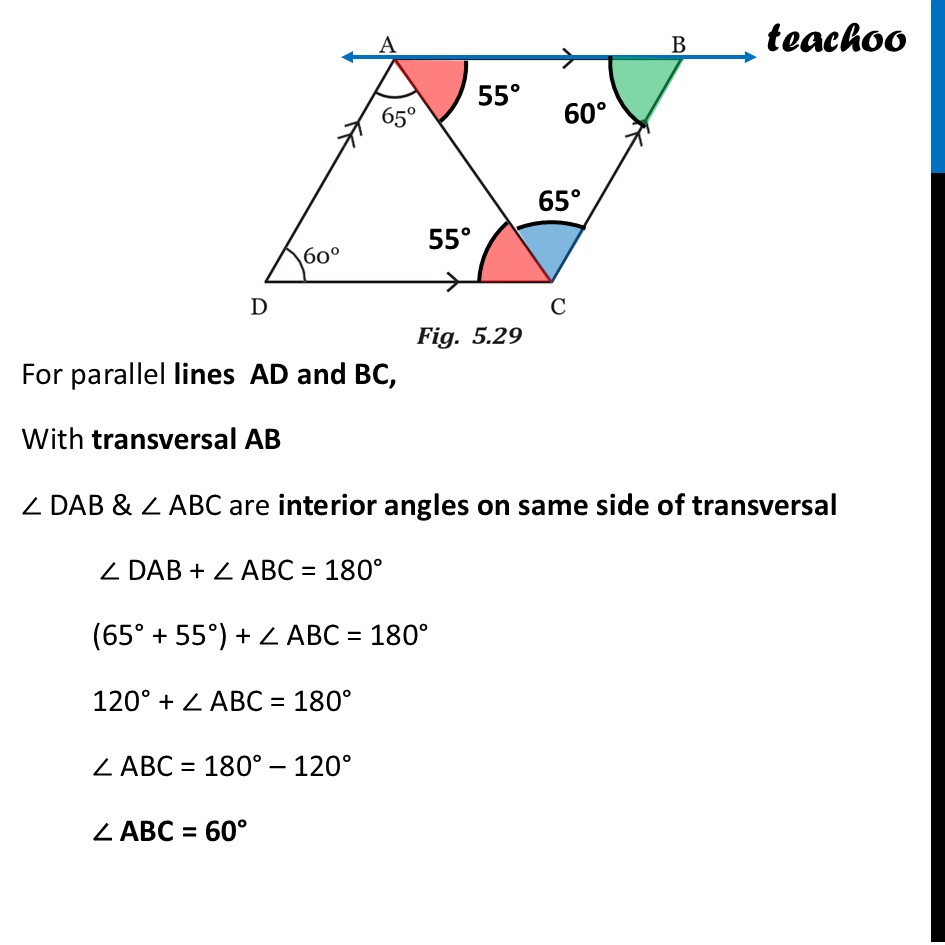
Example 4 - Page 122 In Fig. 5.29, line segment AB is parallel to CD and AD is parallel to BC. ∠DAC is 65° and ∠ADC is 60°. What are the measures of angles ∠CAB, ∠ABC, and ∠BCD? For parallel lines AB and CD, With transversal AC ∠ DAC & ∠ ACB are alternate angles ∴ ∠ ACB = ∠ DAC ∠ ACB = 65° And, ∠ BAC & ∠ DCA are also alternate interior angles ∴ ∠ BAC = ∠ DAC For parallel lines AD and BC, With transversal AB ∠ DAB & ∠ ABC are interior angles on same side of transversal ∠ DAB + ∠ ABC = 180° (65° + 55°) + ∠ ABC = 180° 120° + ∠ ABC = 180° ∠ ABC = 180° – 120° ∠ ABC = 60° For parallel lines AD and BC, With transversal DC ∠ ADC & ∠ BCD are interior angles on same side of transversal ∠ ADC + ∠ BCD = 180° 60° + ∠ BCD = 180° ∠ BCD = 180° – 60° ∠ BCD = 120° And, ∠ BCD = ∠ ACB + ∠ ACD 120° = 65° + ∠ ACD 120° – 65° = ∠ ACD 55° = ∠ ACD ∠ ACD = 55° Therefore, in Fig. 5.29, ∠ CAB = 55°, ∠ ABC = 60°, and ∠ BCD = 120°.