



Transversals
Last updated at July 24, 2025 by Teachoo












Transcript
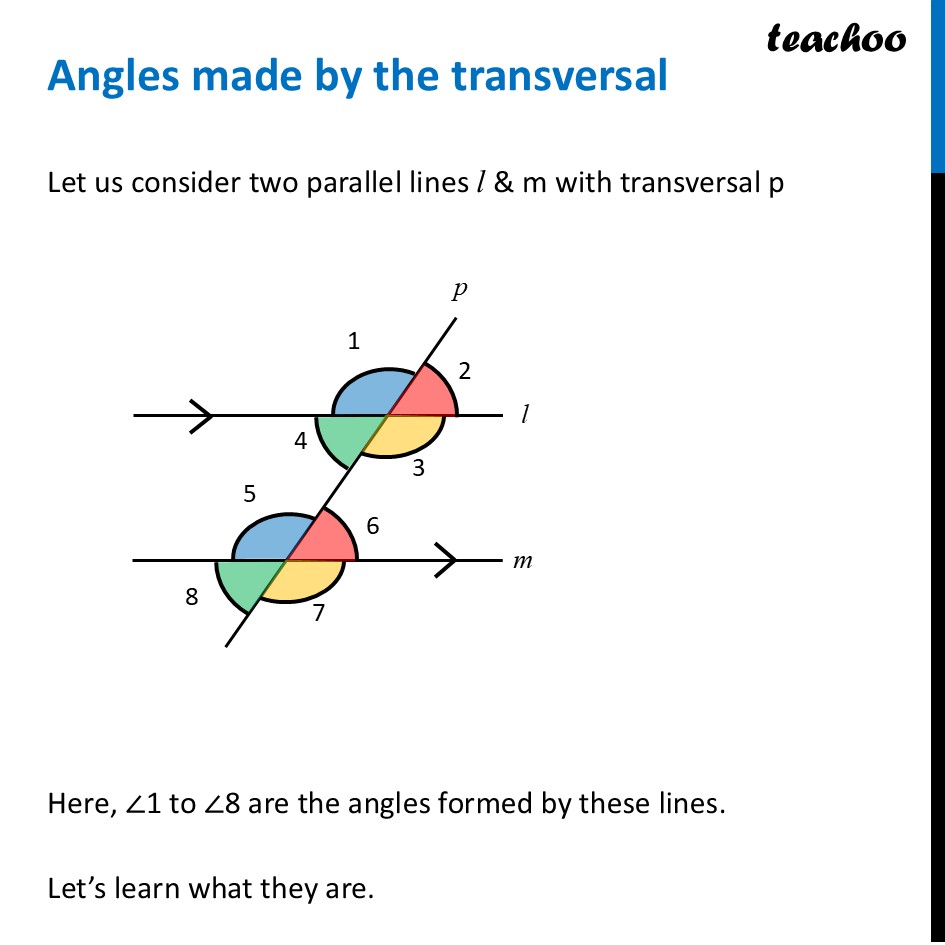
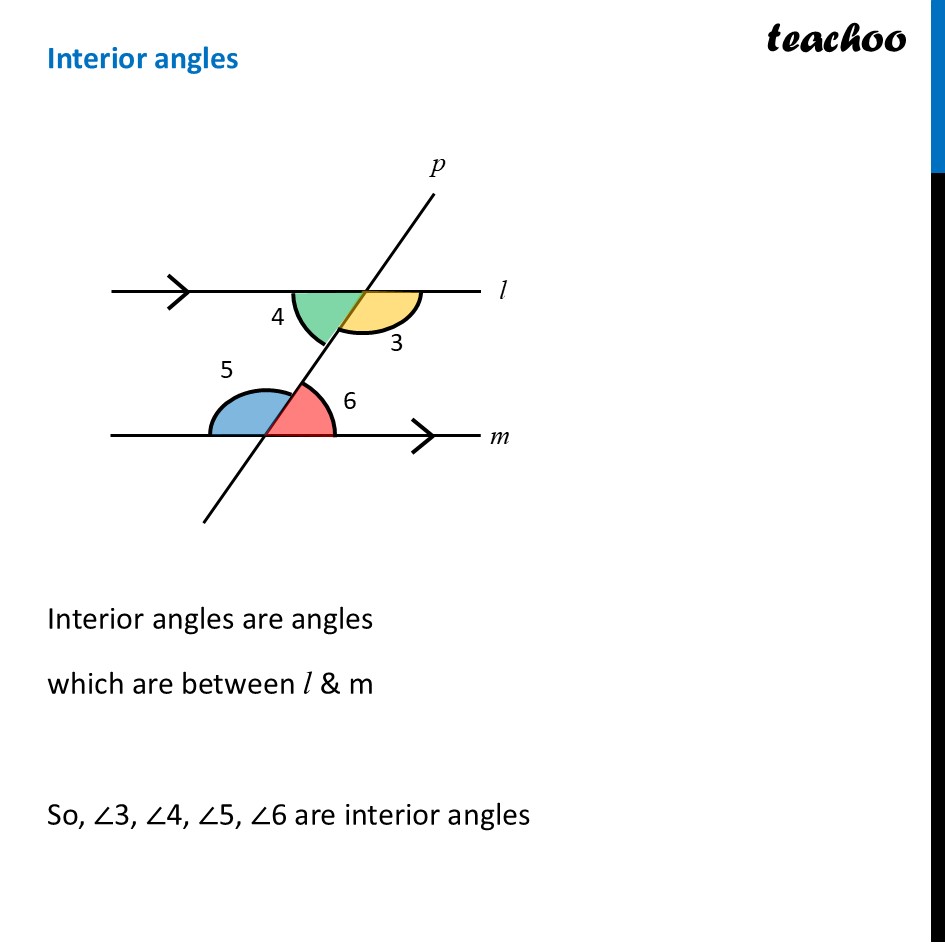
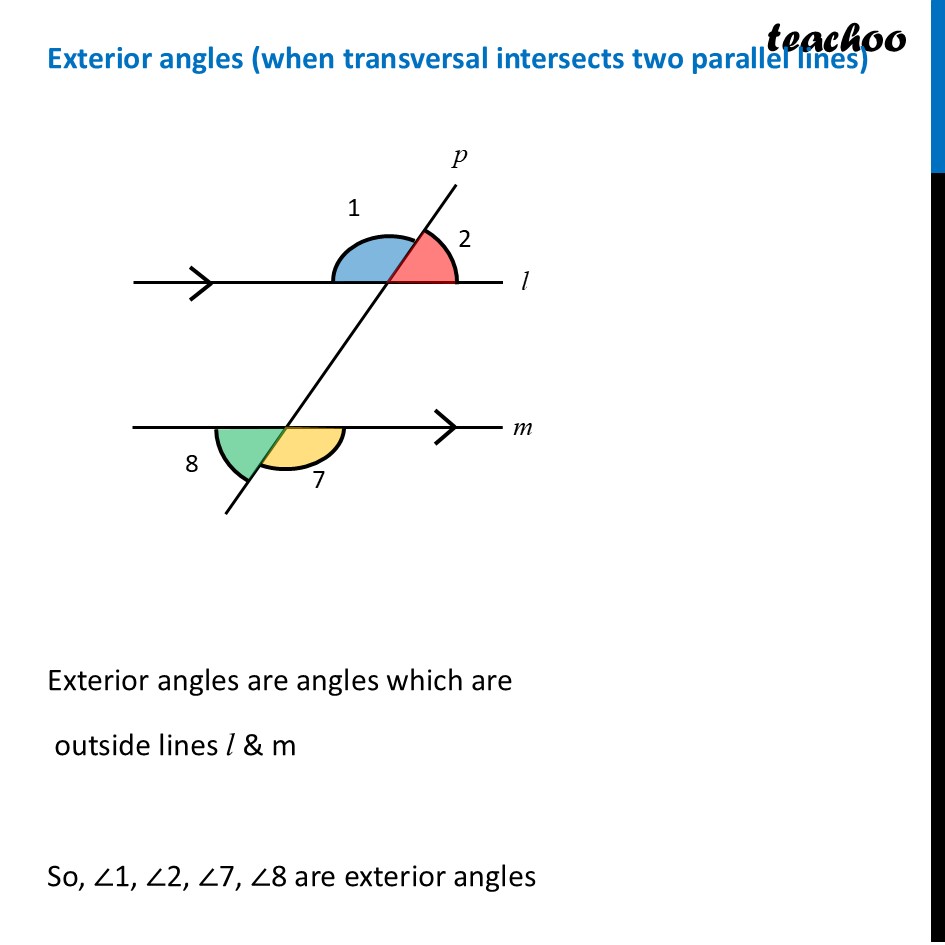
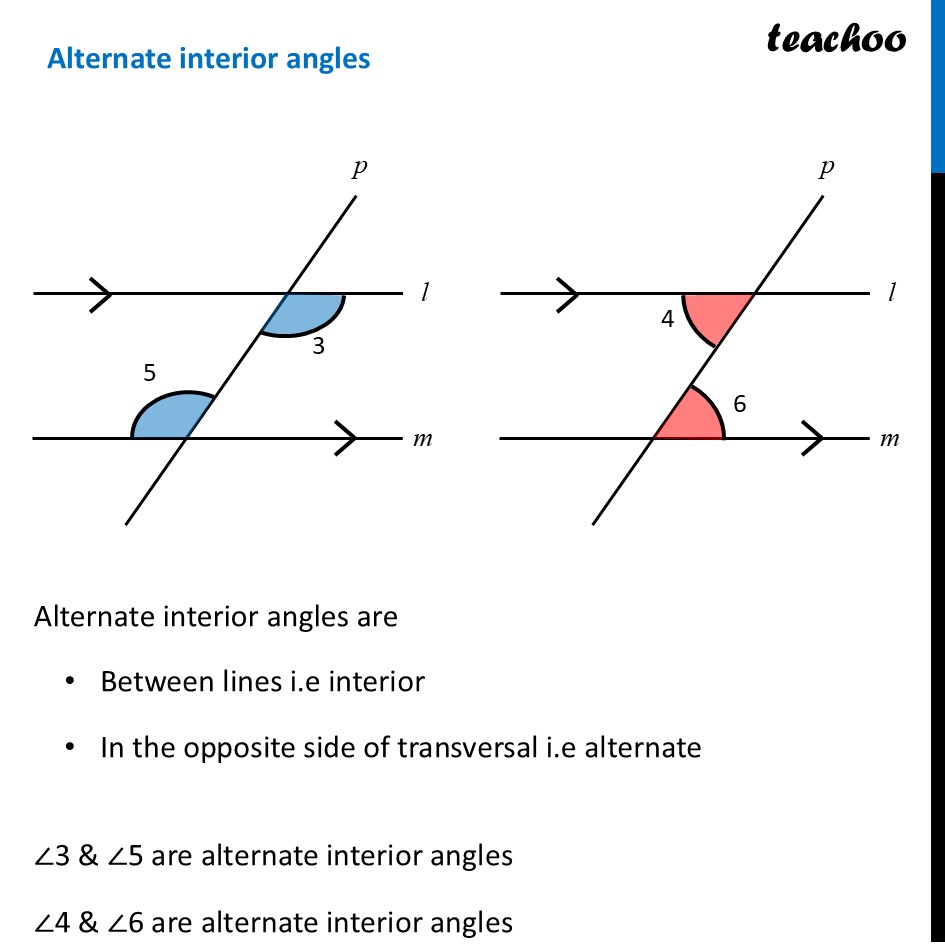
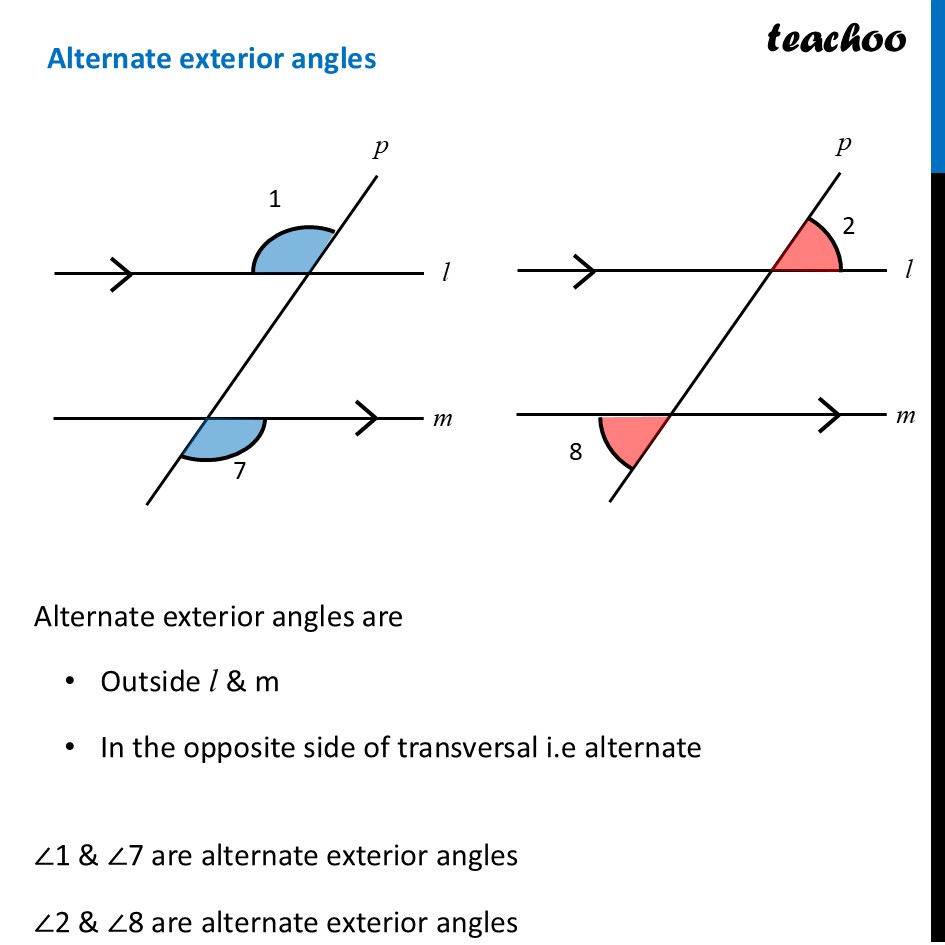
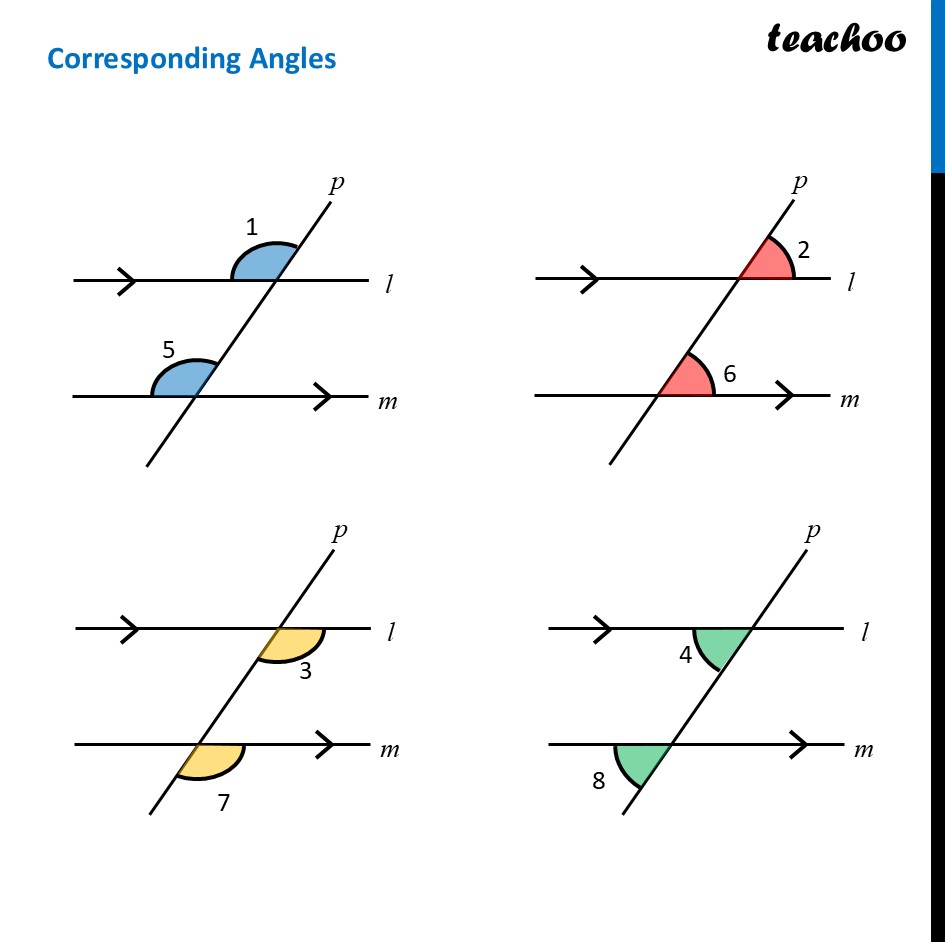
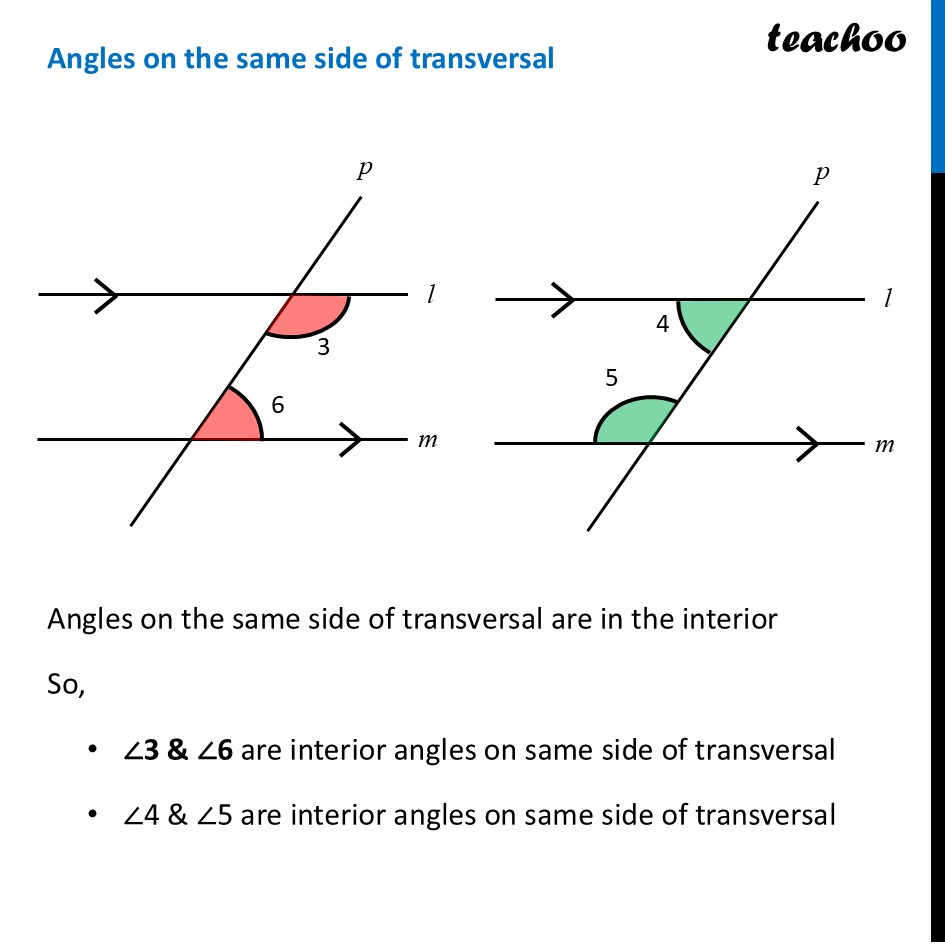
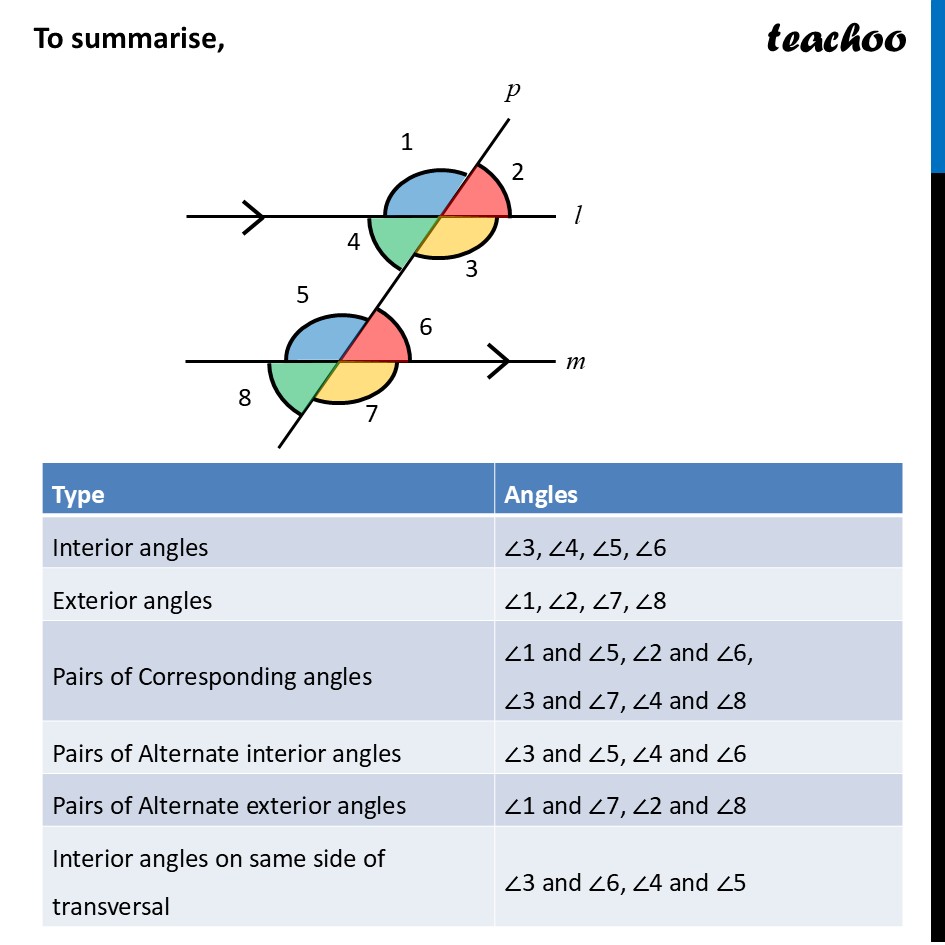
Angles made by the transversalLet us consider two parallel lines l & m with transversal p Here, ∠1 to ∠8 are the angles formed by these lines. Let’s learn what they are. Interior anglesInterior angles are angles which are between l & m So, ∠3, ∠4, ∠5, ∠6 are interior angles Exterior angles (when transversal intersects two parallel lines)Alternate interior anglesAlternate interior angles are Between lines i.e interior In the opposite side of transversal i.e alternate ∠3 & ∠5 are alternate interior angles ∠4 & ∠6 are alternate interior angles For parallel lines, Alternate interior angles are equal. ∠ 3 = ∠ 5 & ∠ 4 = ∠ 6 Alternate exterior anglesAlternate exterior angles are Outside l & m In the opposite side of transversal i.e alternate ∠1 & ∠7 are alternate exterior angles ∠2 & ∠8 are alternate exterior angles For parallel lines, Alternate exterior angles are equal. ∠ 1 = ∠ 7 & ∠ 2 = ∠ 8 Corresponding AnglesCorresponding angles have Different vertices Are on same side of transversal Have corresponding positions i.e. both upper left or lower left or upper right or lower right So, corresponding angles are ∠ 1 and ∠ 5 ∠ 2 and ∠ 6 ∠ 3 and ∠ 7 ∠ 4 and ∠ 8 For parallel lines, corresponding angles are equal Angles on the same side of transversalAngles on the same side of transversal are in the interior So, ∠3 & ∠6 are interior angles on same side of transversal ∠4 & ∠5 are interior angles on same side of transversal For parallel lines, sum of angles on same side of transversal is 180° Therefore, ∠ 3 + ∠ 6 = 180° And, ∠ 4 + ∠ 5 = 180° To summarise,