Ex 10.2, 11 - Chapter 10 Class 10 Circles
Last updated at April 16, 2024 by Teachoo
Theorem 10.2: Equal tangents from external point (proof type)
Chapter 10 Class 10 Circles
Concept wise
- Number of tangents
- Theorem 10.1: Tangent perpendicular to radius (numerical type)
- Theorem 10.1: Tangent perpendicular to radius (proof type)
- Theorem 10.2: Equal tangents from external point (numerical type)
-
Theorem 10.2: Equal tangents from external point (proof type)
Transcript
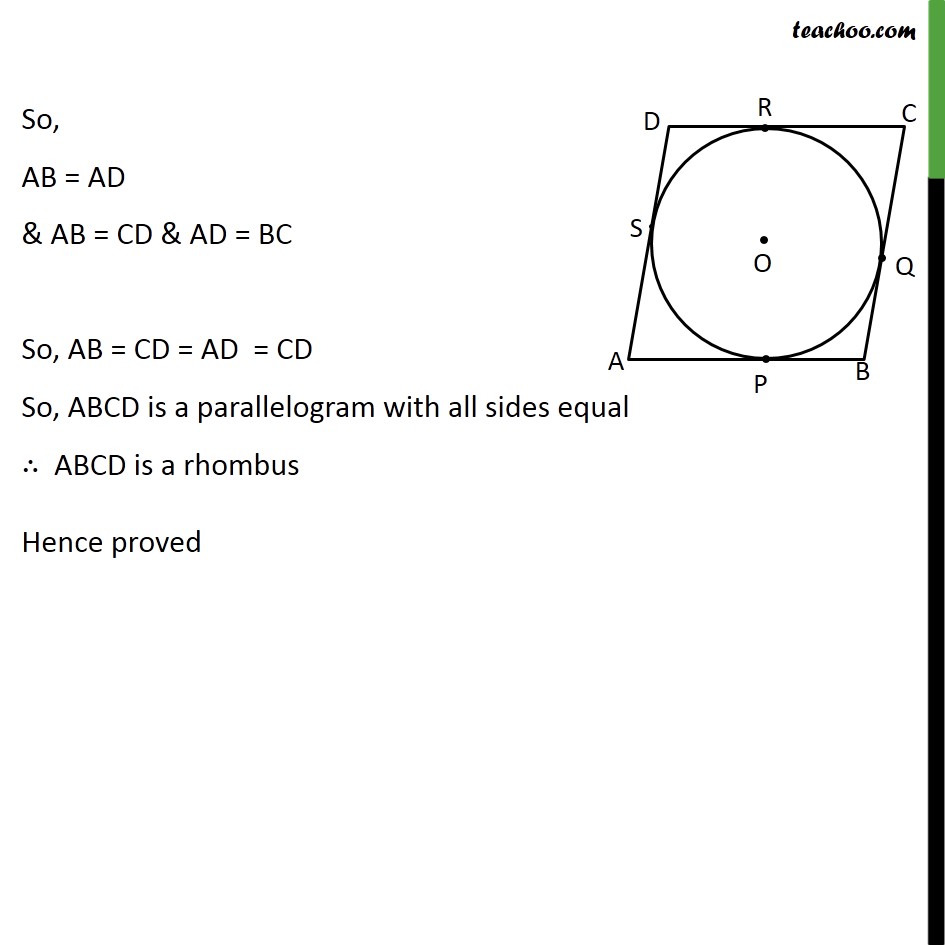
Ex 10.2,11 Prove that the parallelogram circumscribing a circle is a rhombus. Given: A circle with centre O. A parallelogram ABCD touching the circle at points P,Q,R and S To prove: ABCD is a rhombus Proof: A rhombus is a parallelogram with all sides equal, So, we have to prove all sides equal In parallelogram ABCD, AB = CD & AD = BC From theorem 10.2, lengths of tangents drawn from external point are equal Hence, AP = AS BP = BQ CR = CQ DR = DS Adding (2) + (3) + (4) + (5) AP + BP + CR + DR = AS + BQ + CQ + DS (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ) AB + CD = AD + BC AB + AB = AD + AD 2AB = 2AD AB = AD So, AB = AD & AB = CD & AD = BC So, AB = CD = AD = CD So, ABCD is a parallelogram with all sides equal ABCD is a rhombus Hence proved
