You are here
Ex 10.2, 2 (MCQ) - Chapter 10 Class 10 Circles
Last updated at April 16, 2024 by Teachoo
Theorem 10.1: Tangent perpendicular to radius (numerical type)
Chapter 10 Class 10 Circles
Concept wise
- Number of tangents
-
Theorem 10.1: Tangent perpendicular to radius (numerical type)
- Theorem 10.1: Tangent perpendicular to radius (proof type)
- Theorem 10.2: Equal tangents from external point (numerical type)
- Theorem 10.2: Equal tangents from external point (proof type)
Transcript
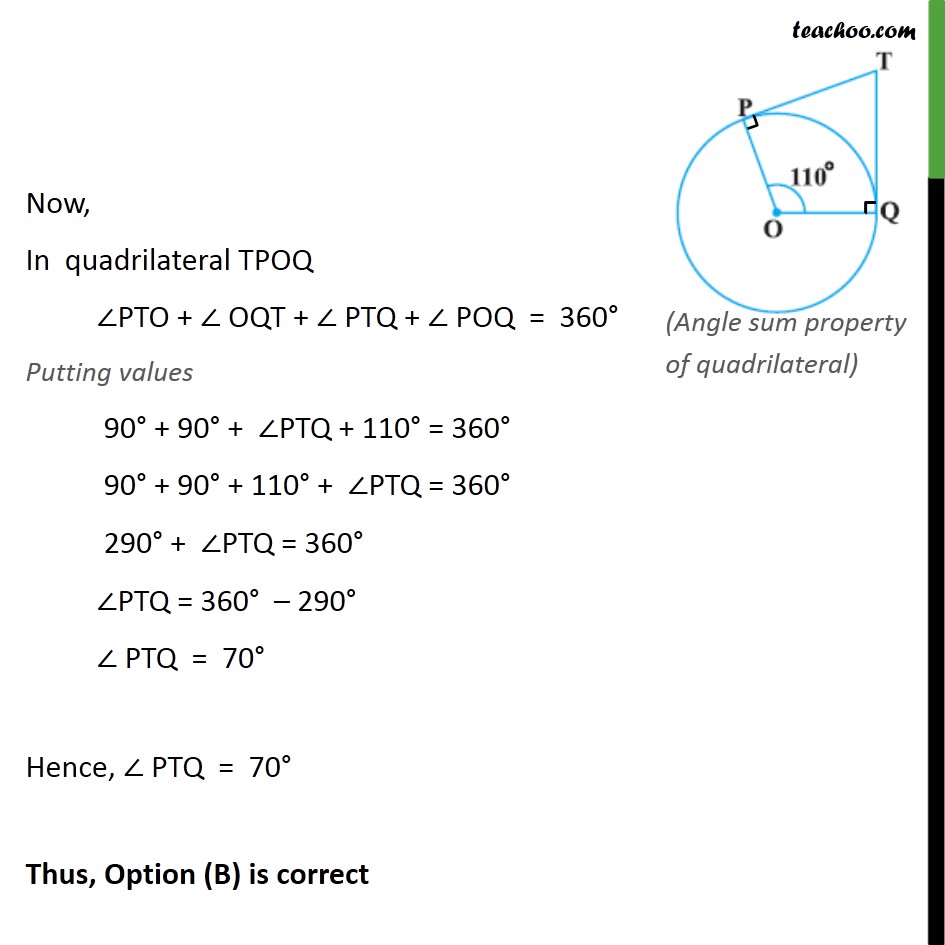
Ex 10.2,2 Choose the correct option and give justification. In figure, if TP and TQ are the two tangents to a circle with centre O so that POQ = 110 , then PTQ is equal to 60 (B) 70 (C) 80 (D) 90 Given POQ = 110 Here TP is a tangent. So, OP TP Hence, OPT = 90 Similarly , TQ is a tangent. So, OQ TQ Hence, OQT = 90 Now, In quadrilateral TPOQ PTO + OQT + PTQ + POQ = 360 Putting values 90 + 90 + PTQ + 110 = 360 90 + 90 + 110 + PTQ = 360 290 + PTQ = 360 PTQ = 360 290 PTQ = 70 Hence, PTQ = 70 Thus, Option (B) is correct
