Question 4 - Paralleograms & triangles with same base & same parallel lines - Areas of Parallelograms and Triangles

Transcript

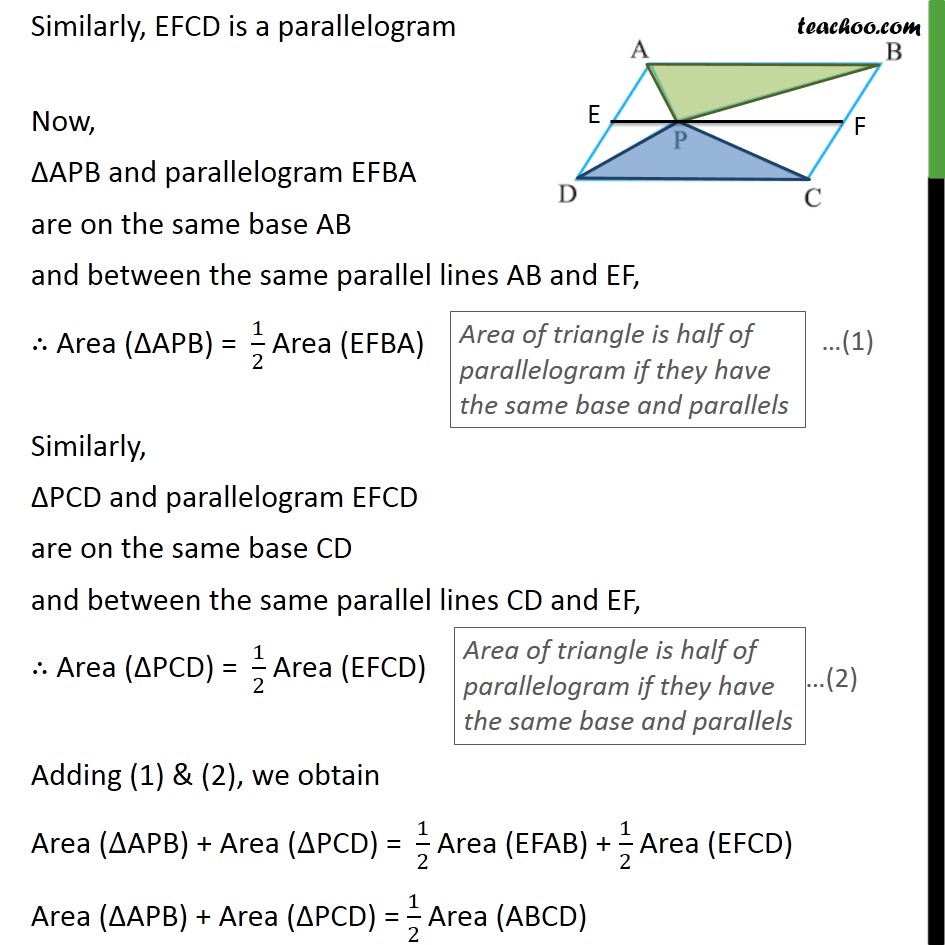
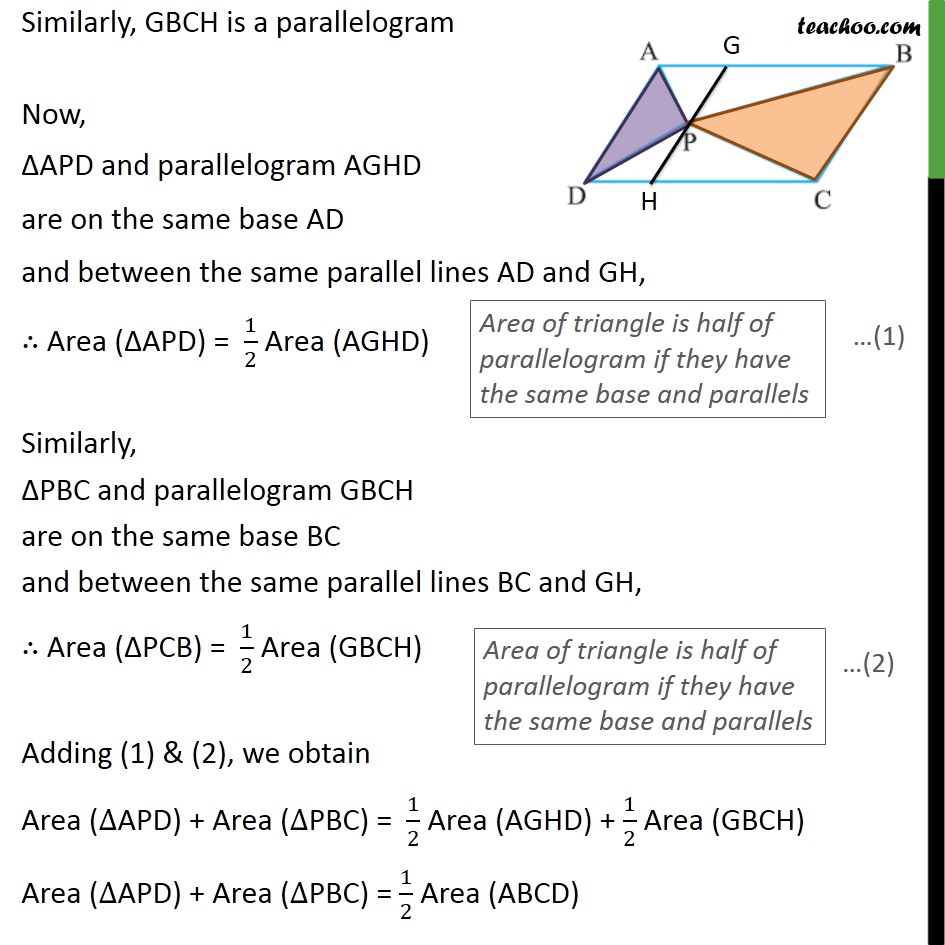
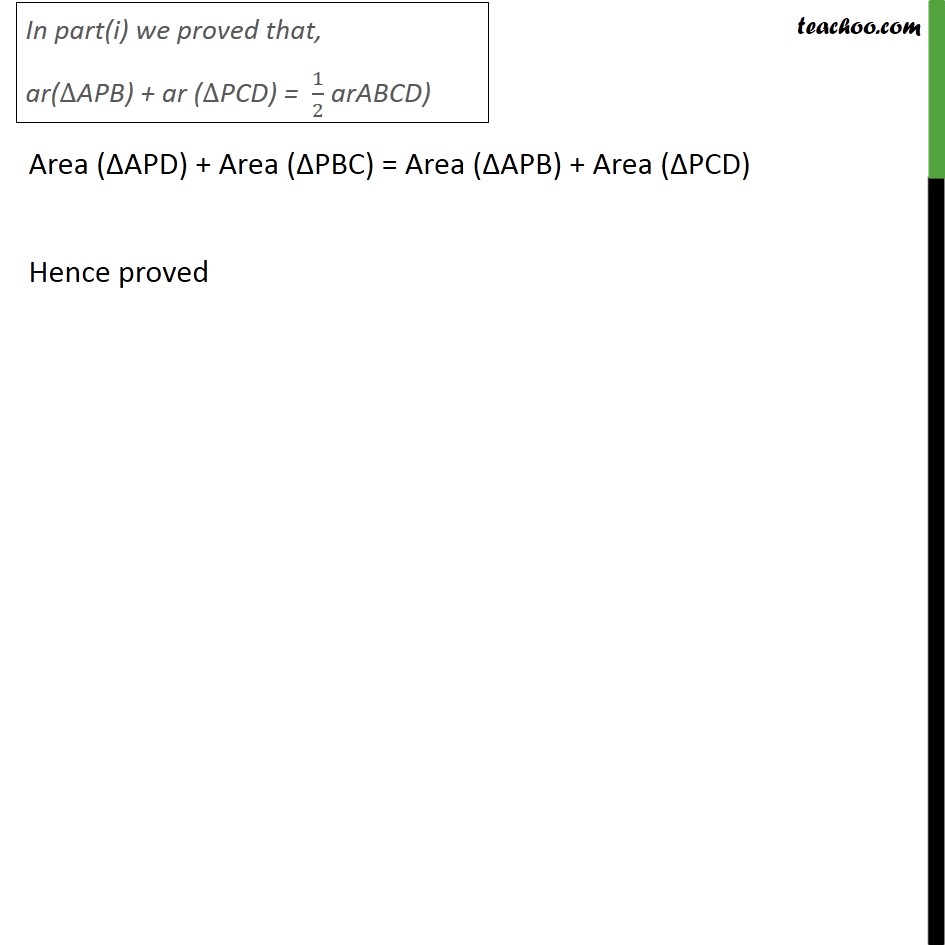
Question 4 In the given figure, P is a point in the interior of a parallelogram ABCD. Show that ar (APB) + ar (PCD) = 1/2 ar (ABCD) Given: A parallelogram ABCD To prove: ar (APB) + ar(PCD) = 1/2 ar (ABCD) Proof: Since ABCD is a parallelogram AB ∥ CD & AD ∥ BC We draw line EF passing through P, parallel to AB & DC i.e. EF ∥ AB ∥ CD Here, AE ∥ BF & AB ∥ EF ∴ EFBA is a parallelogram Similarly, EFCD is a parallelogram Now, ΔAPB and parallelogram EFBA are on the same base AB and between the same parallel lines AB and EF, ∴ Area (ΔAPB) = 1/2 Area (EFBA) Similarly, ΔPCD and parallelogram EFCD are on the same base CD and between the same parallel lines CD and EF, ∴ Area (ΔPCD) = 1/2 Area (EFCD) Adding (1) & (2), we obtain Area (∆APB) + Area (∆PCD) = 1/2 Area (EFAB) + 1/2 Area (EFCD) Area (ΔAPB) + Area (ΔPCD) = 1/2 Area (ABCD) Question 4 In the given figure, P is a point in the interior of a parallelogram ABCD. Show that (ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD) Given: A parallelogram ABCD To prove: ar (APD) + ar(PBC) =ar (APB) + ar (PCD) Proof: Since ABCD is a parallelogram AB ∥ CD & AD ∥ BC We draw line GH passing through P, parallel to AD & BC i.e. GH ∥ AD ∥ BC Here, GH ∥ AD & AG ∥ DH ∴ AGHD is a parallelogram Similarly, GBCH is a parallelogram Now, ΔAPD and parallelogram AGHD are on the same base AD and between the same parallel lines AD and GH, ∴ Area (ΔAPD) = 1/2 Area (AGHD) Similarly, ΔPBC and parallelogram GBCH are on the same base BC and between the same parallel lines BC and GH, ∴ Area (ΔPCB) = 1/2 Area (GBCH) Adding (1) & (2), we obtain Area (∆APD) + Area (∆PBC) = 1/2 Area (AGHD) + 1/2 Area (GBCH) Area (∆APD) + Area (∆PBC) = 1/2 Area (ABCD) Area (ΔAPD) + Area (ΔPBC) = Area (ΔAPB) + Area (ΔPCD) Hence proved