Question 2 - Figure it out - Page 235 - Chapter 9 Class 6 - Symmetry (Ganita Prakash)

Transcript

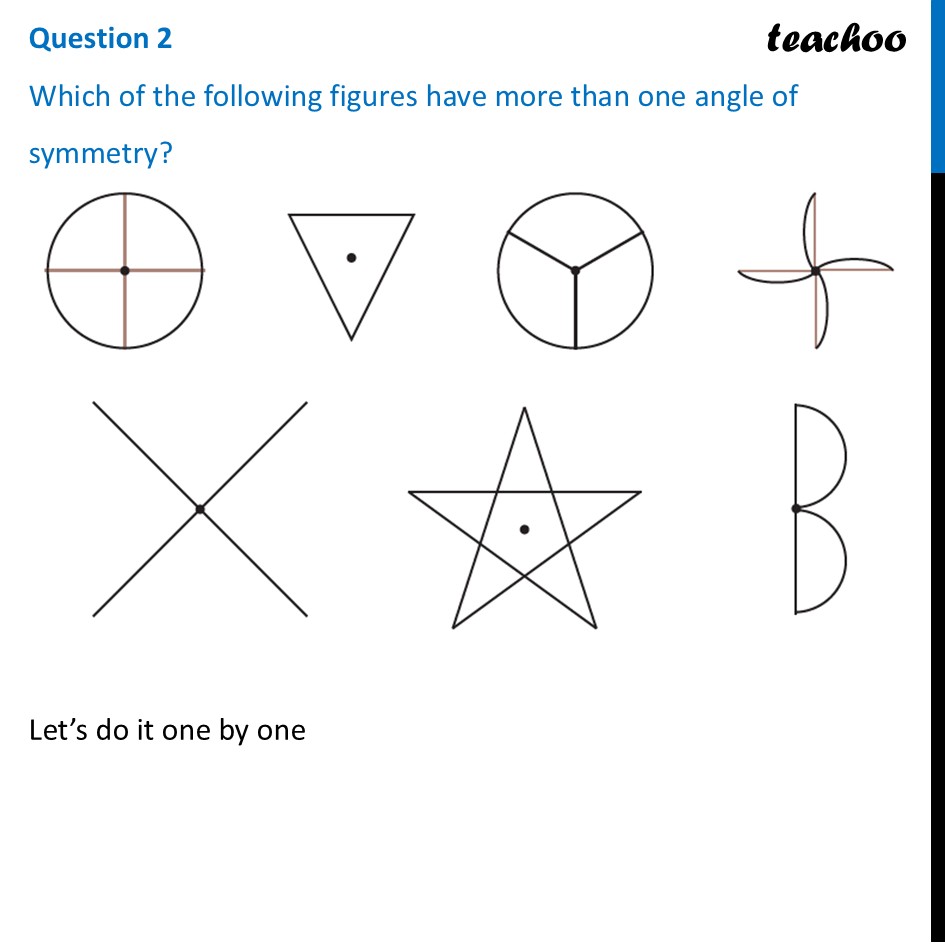
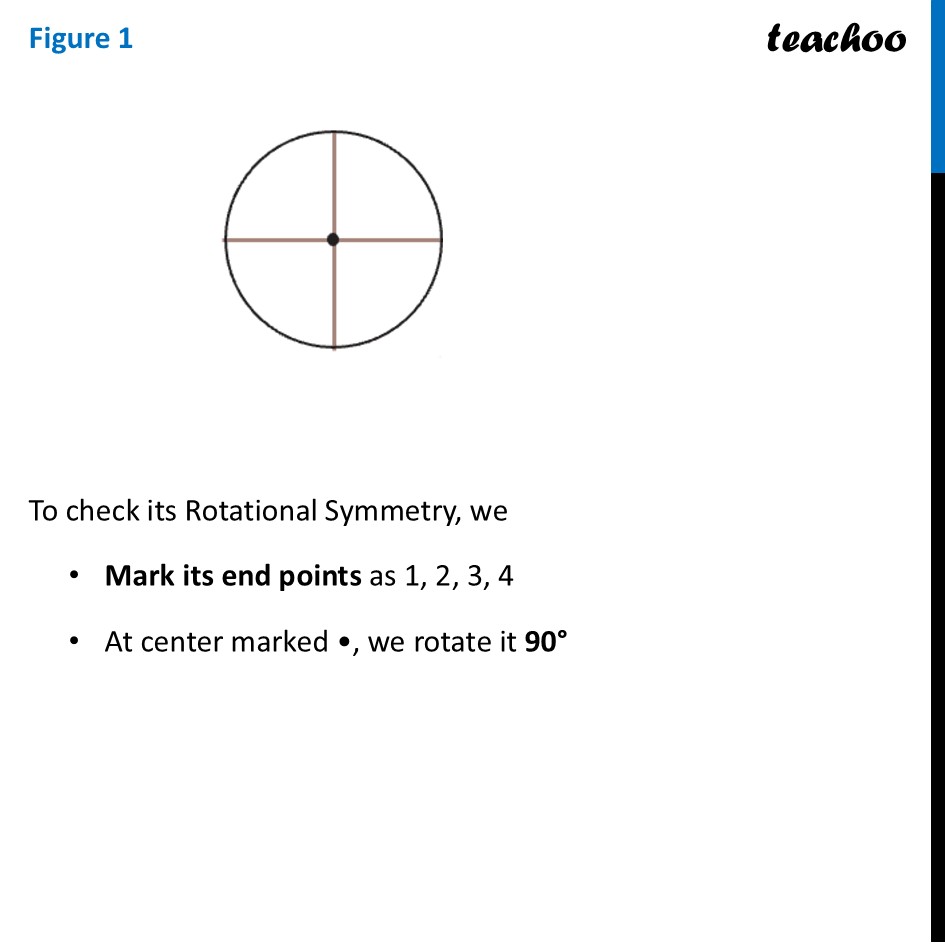
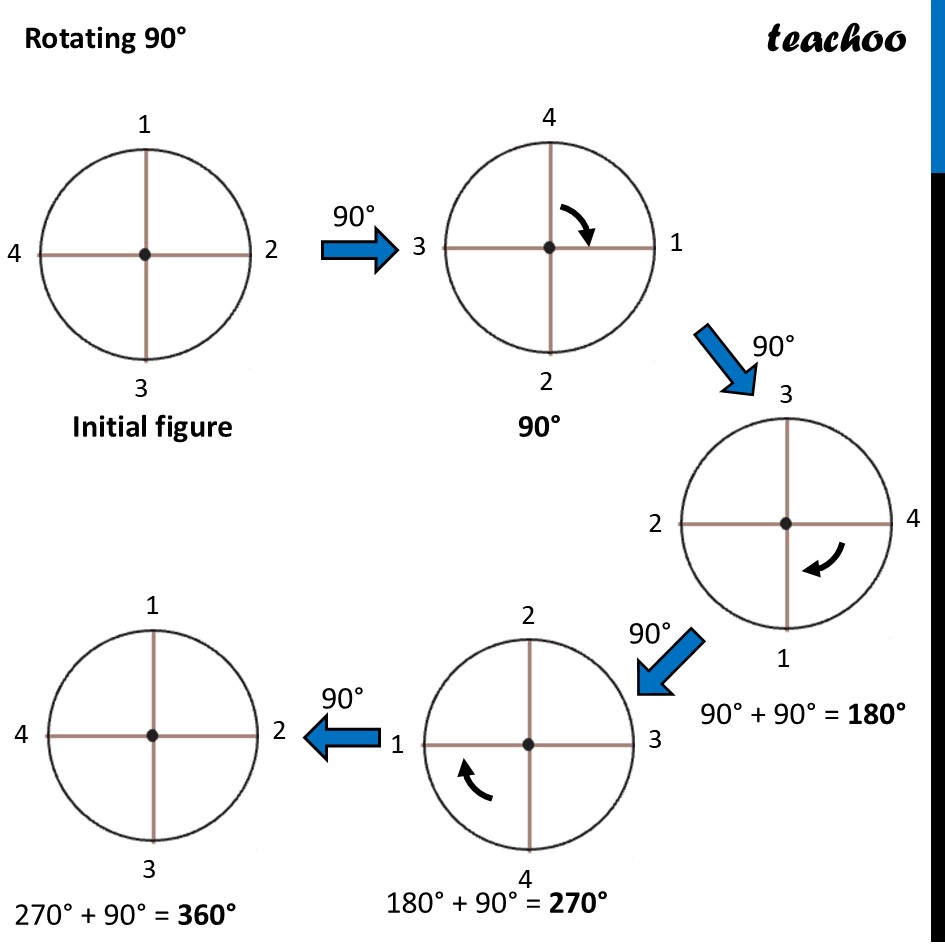
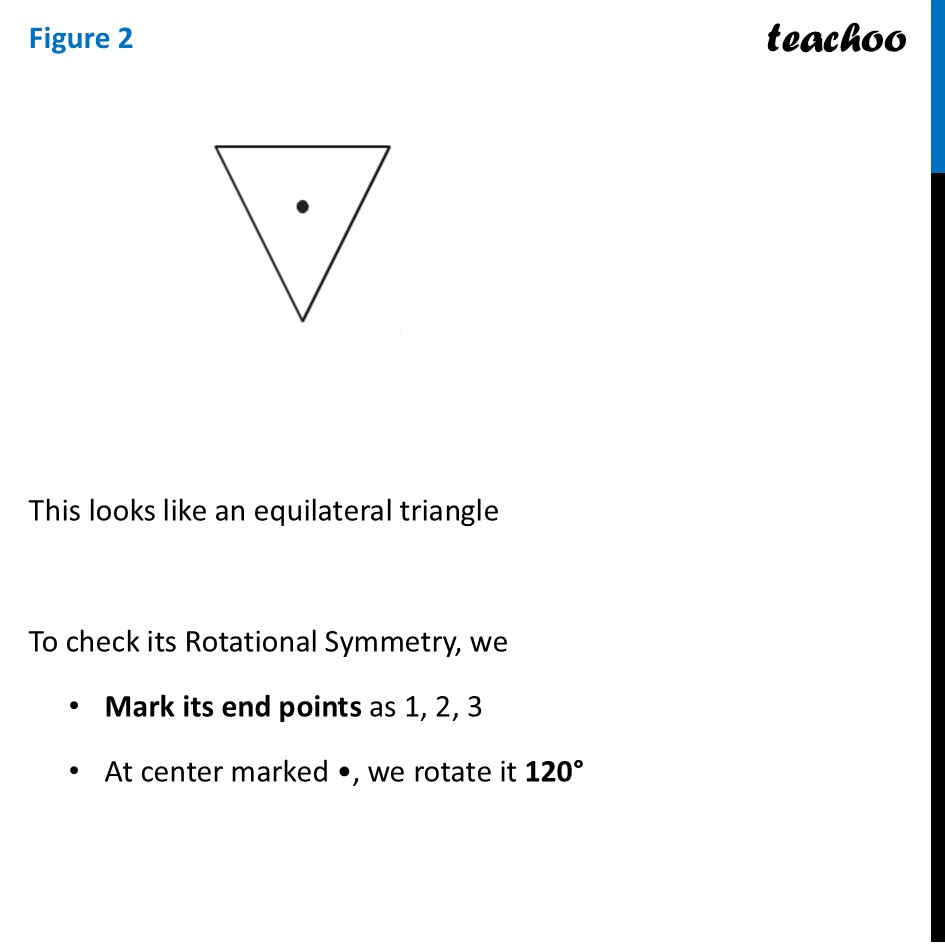
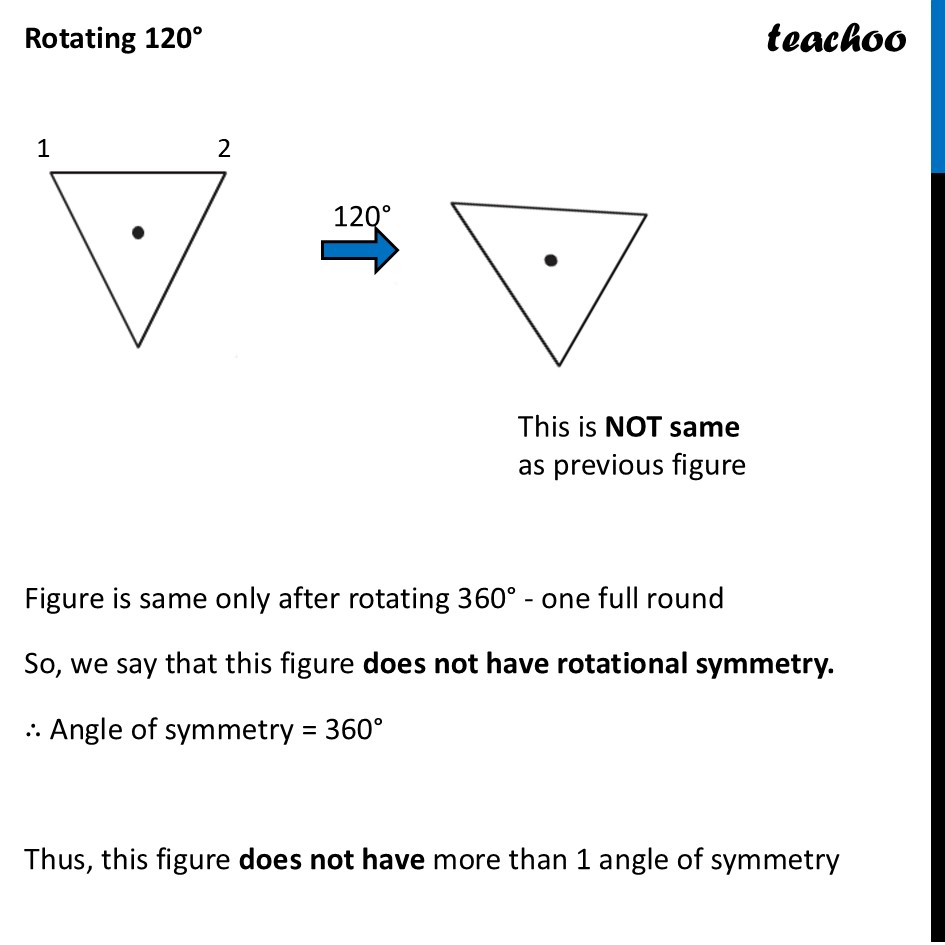
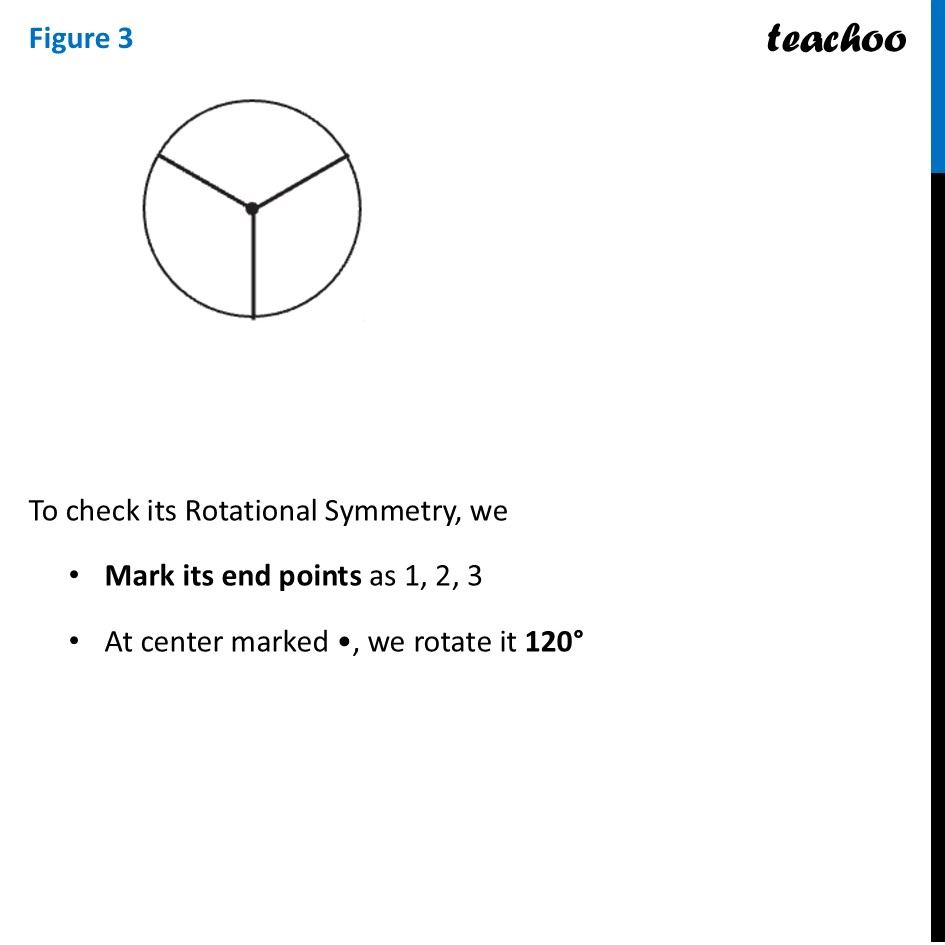
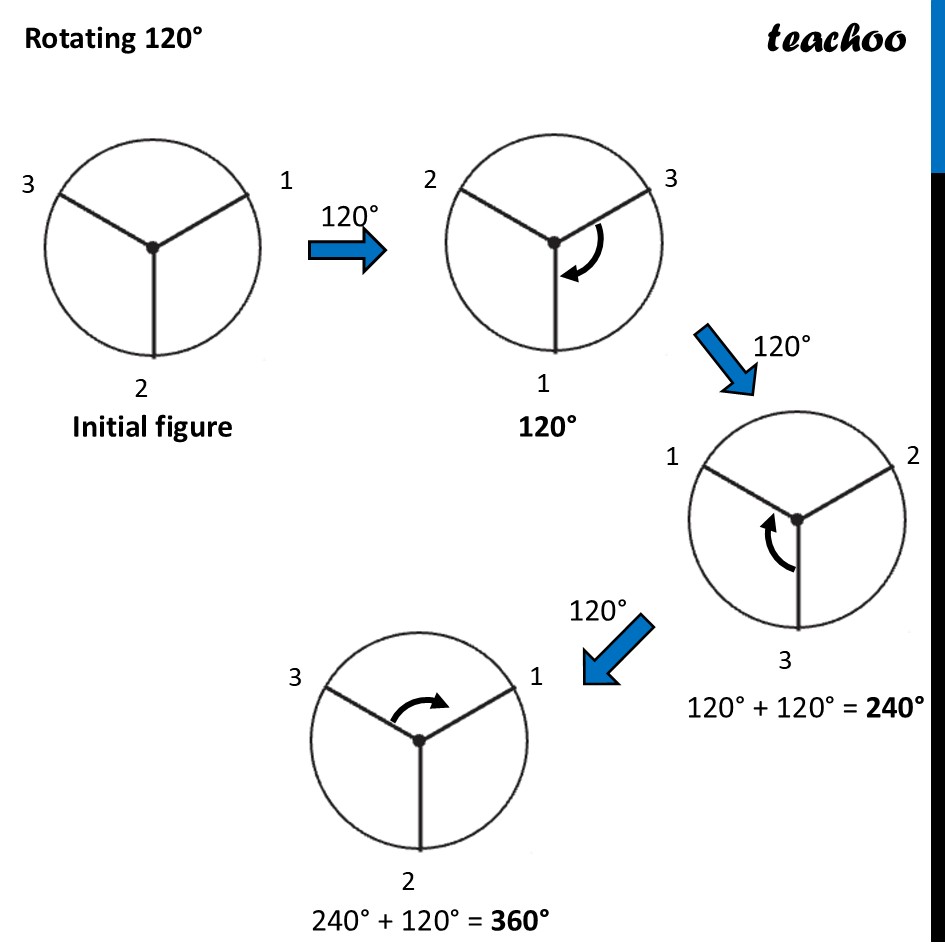
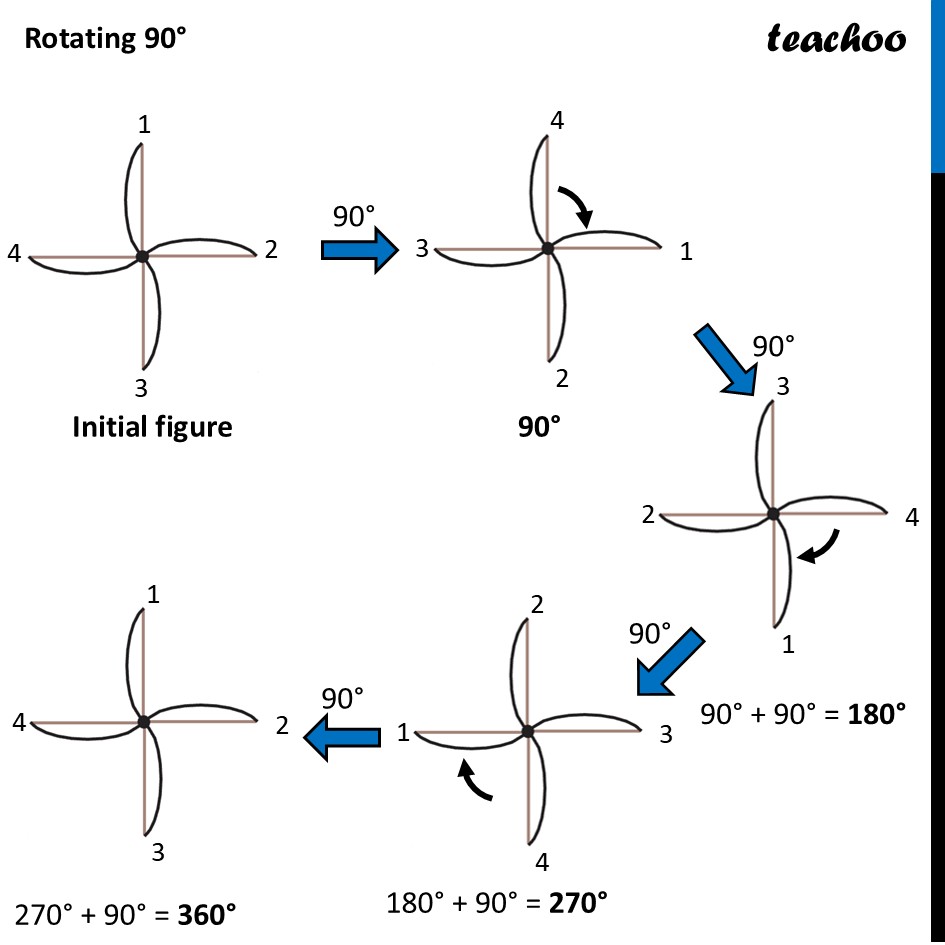
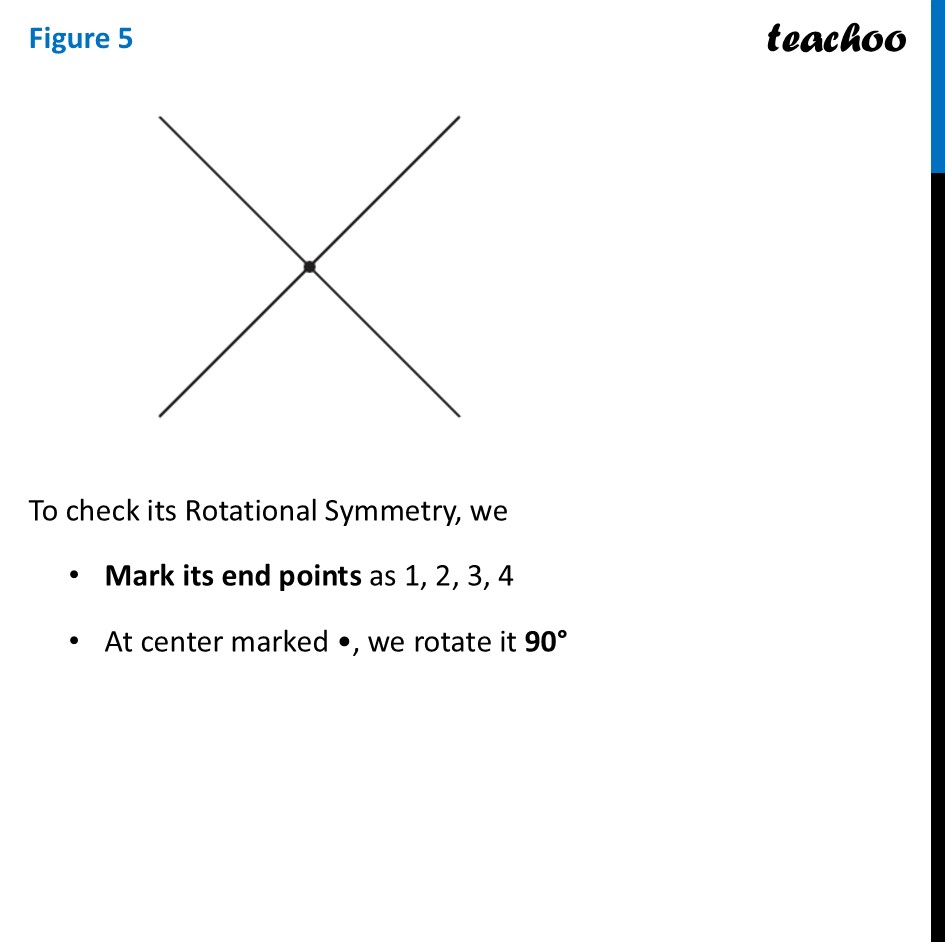
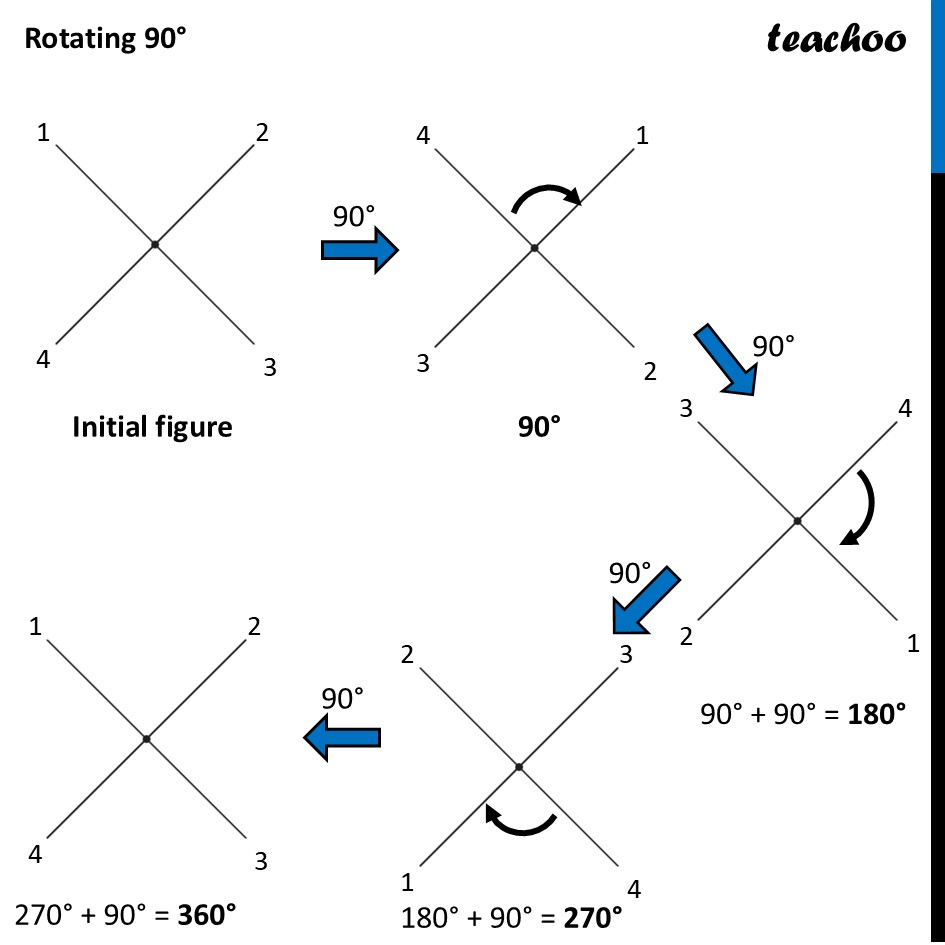
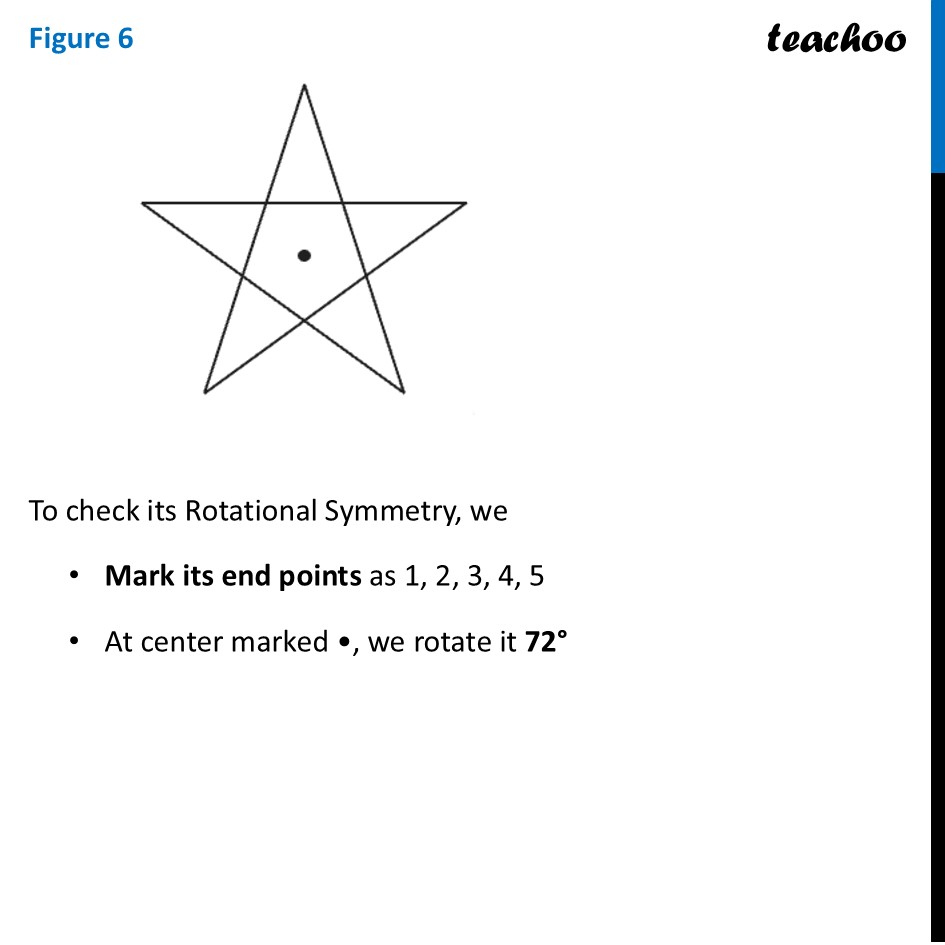
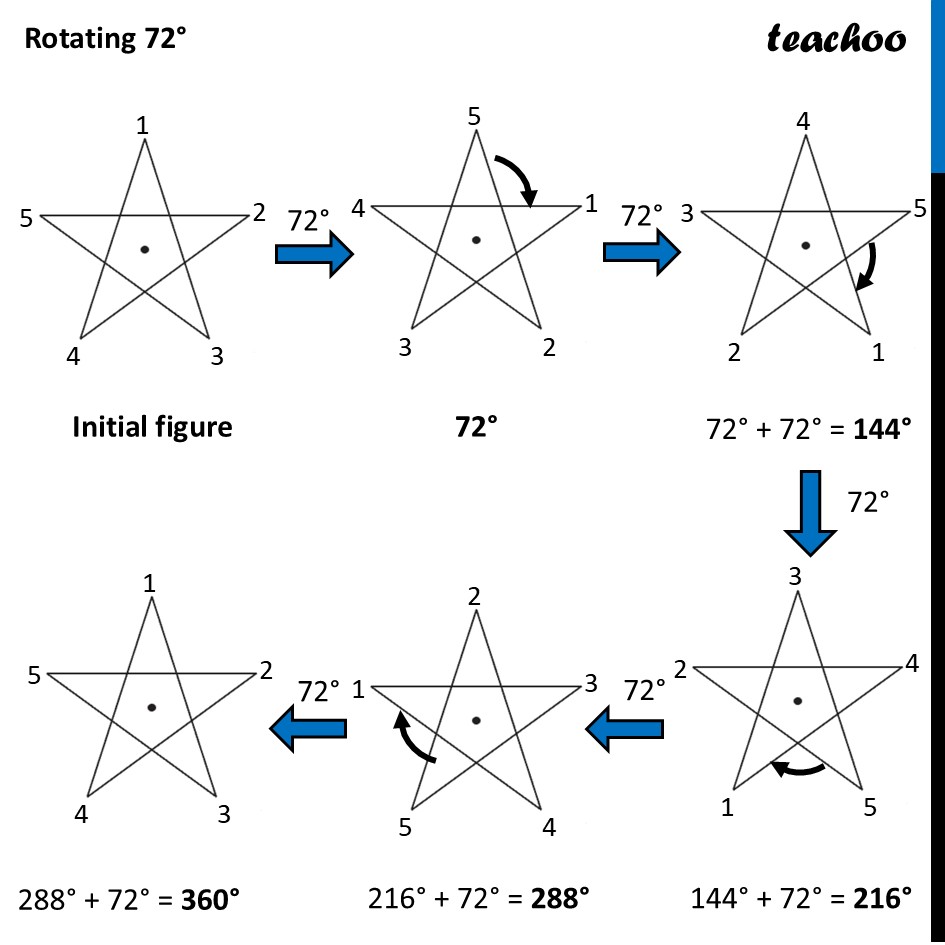
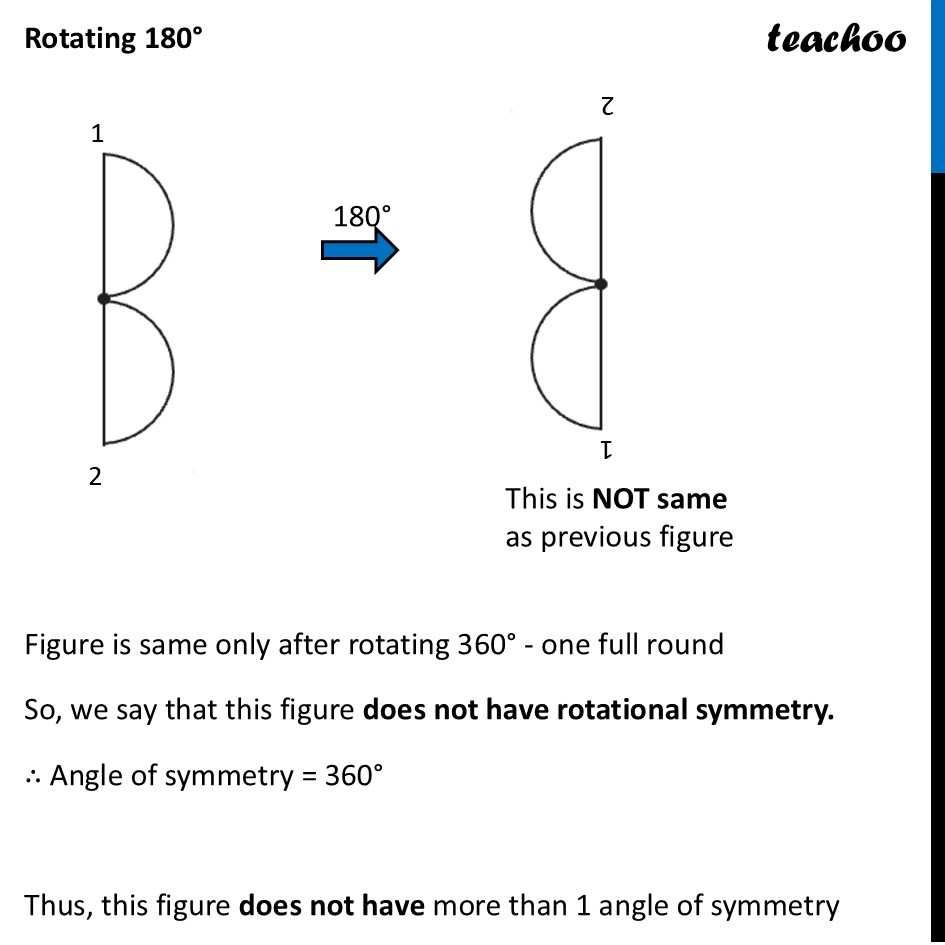
Question 2 Which of the following figures have more than one angle of symmetry?Let’s do it one by one Figure 1To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4 At center marked •, we rotate it 90° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 4 times So, we say that figure has Rotational Symmetry of order 4 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/4 = 90° Thus, the figure would be same at angles 90° 90° × 2 = 180° 90° × 3 = 270° 90° × 4 = 360° So, we write Angles of symmetry = 90°, 180°, 270°, 360° Thus, this figure has more than 1 angle of symmetry This looks like an equilateral triangle To check its Rotational Symmetry, we Mark its end points as 1, 2, 3 At center marked •, we rotate it 120° Figure is same only after rotating 360° - one full round So, we say that this figure does not have rotational symmetry. ∴ Angle of symmetry = 360° Thus, this figure does not have more than 1 angle of symmetry This is NOT same as previous figure To check its Rotational Symmetry, we Mark its end points as 1, 2, 3 At center marked •, we rotate it 120° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 3 times So, we say that figure has Rotational Symmetry of order 3 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/4 = 120° Thus, the figure would be same at angles 120° 120° × 2 = 240° 120° × 3 = 360° So, we write Angles of symmetry = 120°, 240° 360° Thus, this figure has more than 1 angle of symmetry To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4 At center marked •, we rotate it 90° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 4 times So, we say that figure has Rotational Symmetry of order 4 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/4 = 90° Thus, the figure would be same at angles 90° 90° × 2 = 180° 90° × 3 = 270° 90° × 4 = 360° So, we write Angles of symmetry = 90°, 180°, 270°, 360° Thus, this figure has more than 1 angle of symmetry To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4 At center marked •, we rotate it 90° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 4 times So, we say that figure has Rotational Symmetry of order 4 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/4 = 90° Thus, the figure would be same at angles 90° 90° × 2 = 180° 90° × 3 = 270° 90° × 4 = 360° So, we write Angles of symmetry = 90°, 180°, 270°, 360° Thus, this figure has more than 1 angle of symmetry To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4, 5 At center marked •, we rotate it 72° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 5 times So, we say that figure has Rotational Symmetry of order 5 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/5 = 72° Thus, the figure would be same at angles 72° 72° × 2 = 144° 72° × 3 = 216° 72° × 4 = 288° 72° × 5 = 360° So, we write Angles of symmetry = 72°, 144°, 216°, 288°,360° To check its Rotational Symmetry, we Mark its end points as 1, 2 At center marked •, we rotate it 180° Figure is same only after rotating 360° - one full round So, we say that this figure does not have rotational symmetry. ∴ Angle of symmetry = 360° Thus, this figure does not have more than 1 angle of symmetry This is NOT same as previous figure