Question 1 - Figure it out - Page 235 - Chapter 9 Class 6 - Symmetry (Ganita Prakash)

Transcript

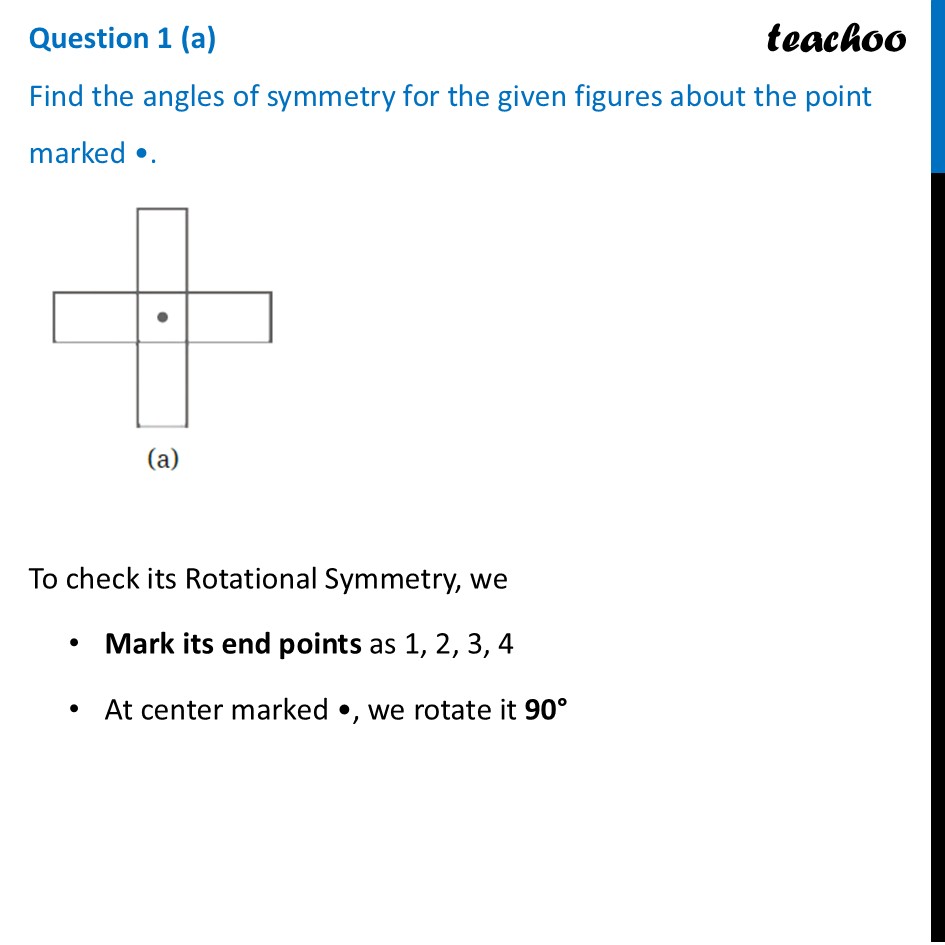
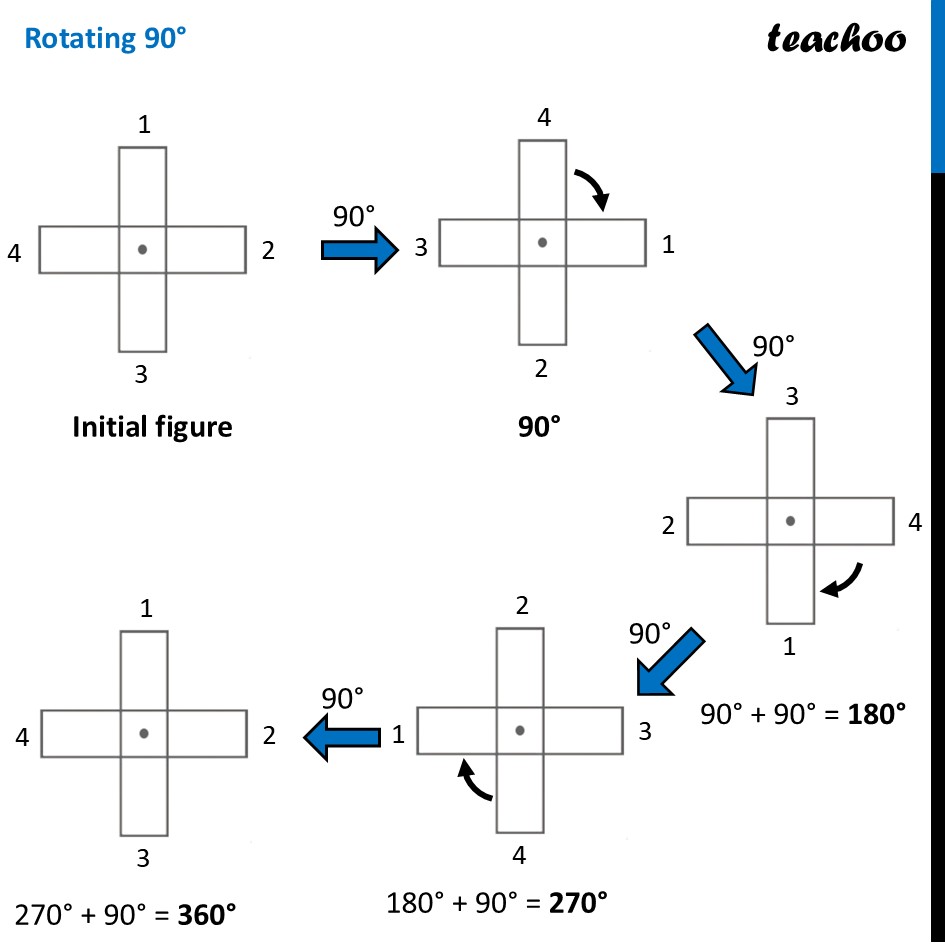
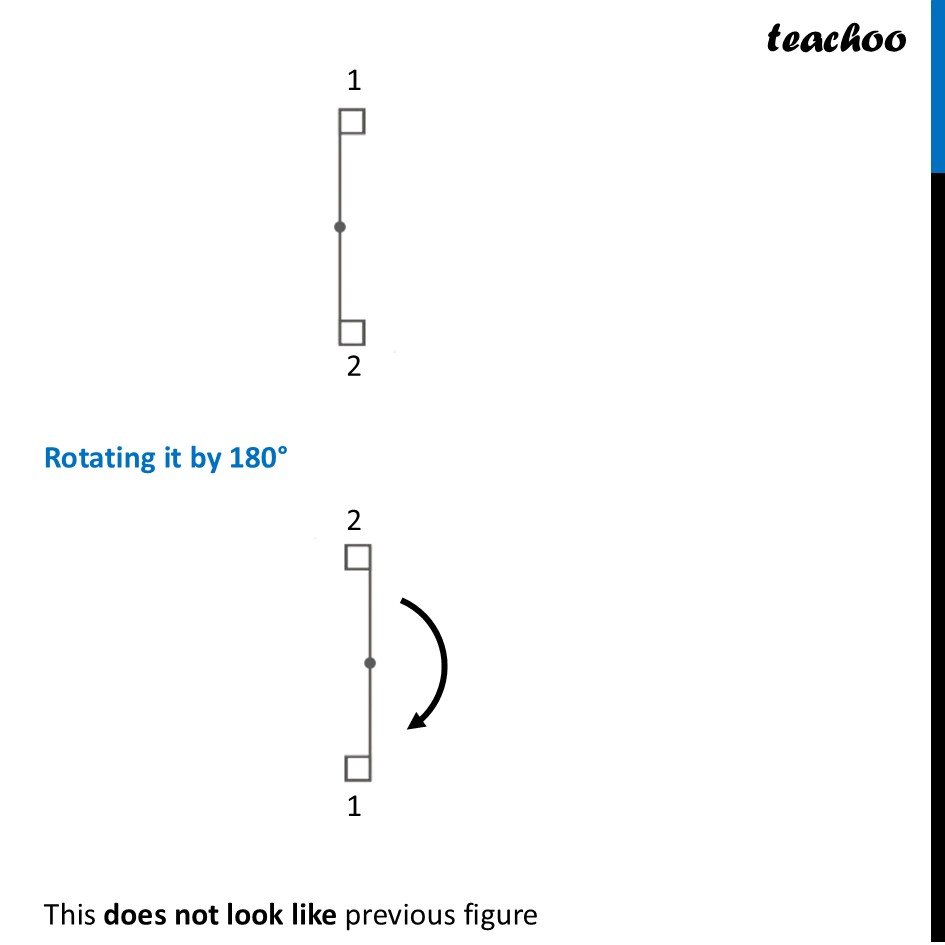
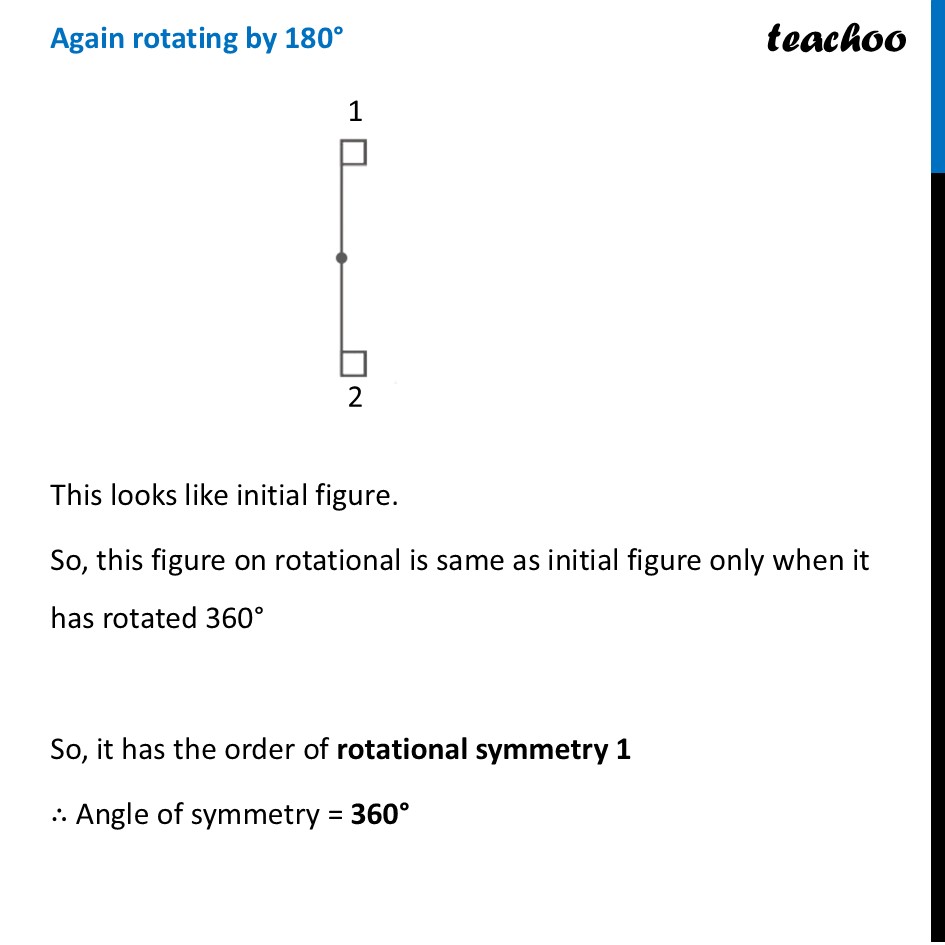
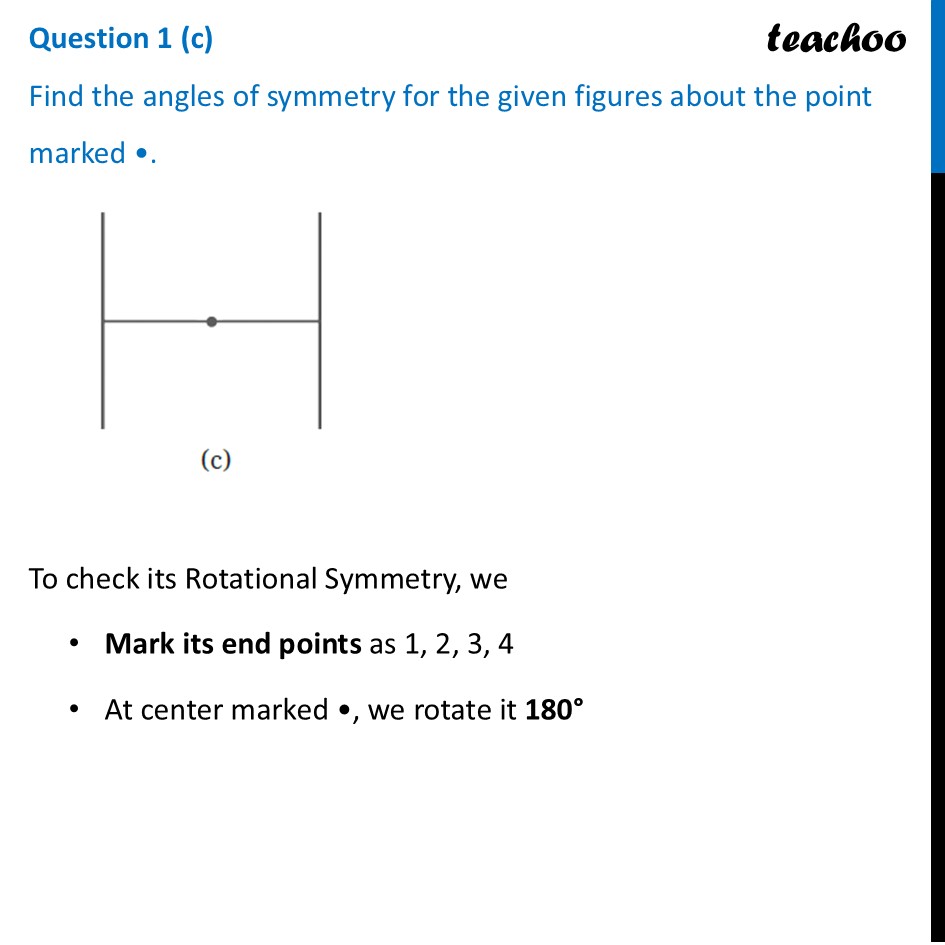
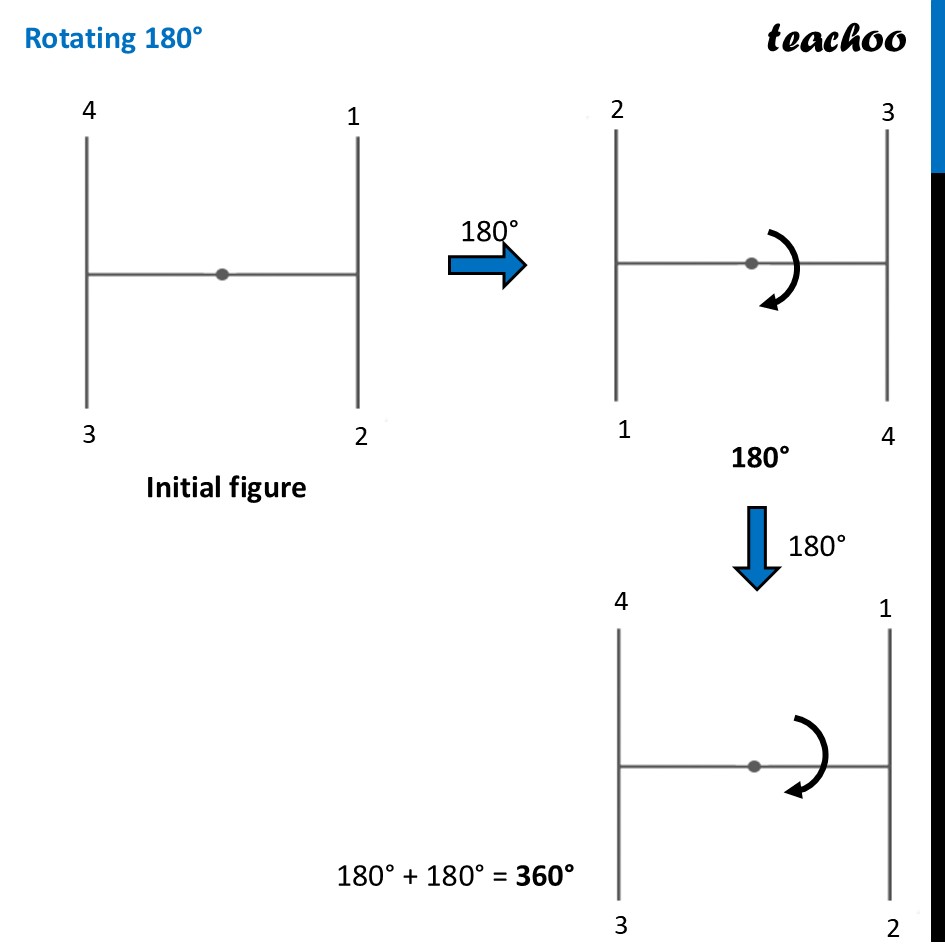
Question 1 (a) Find the angles of symmetry for the given figures about the point marked •.To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4 At center marked •, we rotate it 90° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 4 times So, we say that figure has Rotational Symmetry of order 4 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/4 = 90° Thus, the figure would be same at angles 90° 90° × 2 = 180° 90° × 3 = 270° 90° × 4 = 360° So, we write Angles of symmetry = 90°, 180°, 270°, 360° Question 1 (b) Find the angles of symmetry for the given figures about the point marked •.To check its Rotational Symmetry, we Mark its end points as 1, 2 At center marked •, we rotate it 180° Rotating it by 180° This does not look like previous figure Again rotating by 180° This looks like initial figure. So, this figure on rotational is same as initial figure only when it has rotated 360° So, it has the order of rotational symmetry 1 ∴ Angle of symmetry = 360° Question 1 (c) Find the angles of symmetry for the given figures about the point marked •.To check its Rotational Symmetry, we Mark its end points as 1, 2, 3, 4 At center marked •, we rotate it 180° Rotating 180° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 2 times So, we say that figure has Rotational Symmetry of order 2 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/2 = 180° Thus, the figure would be same at angles 180° 180° × 2 = 360° Thus, in 1 full turn (i.e 360°) The figure is same as that of initial 2 times So, we say that figure has Rotational Symmetry of order 2 And, Angle of symmetry = (𝟑𝟔𝟎° )/(𝑶𝒓𝒅𝒆𝒓 𝒐𝒇 𝑹𝒐𝒕𝒂𝒕𝒊𝒐𝒏𝒂𝒍 𝑺𝒚𝒎𝒎𝒆𝒕𝒓𝒚) = (360° )/2 = 180° Thus, the figure would be same at angles 180° 180° × 2 = 360°