Ex 12.3, 4 - Chapter 12 Class 7 Symmetry

Transcript

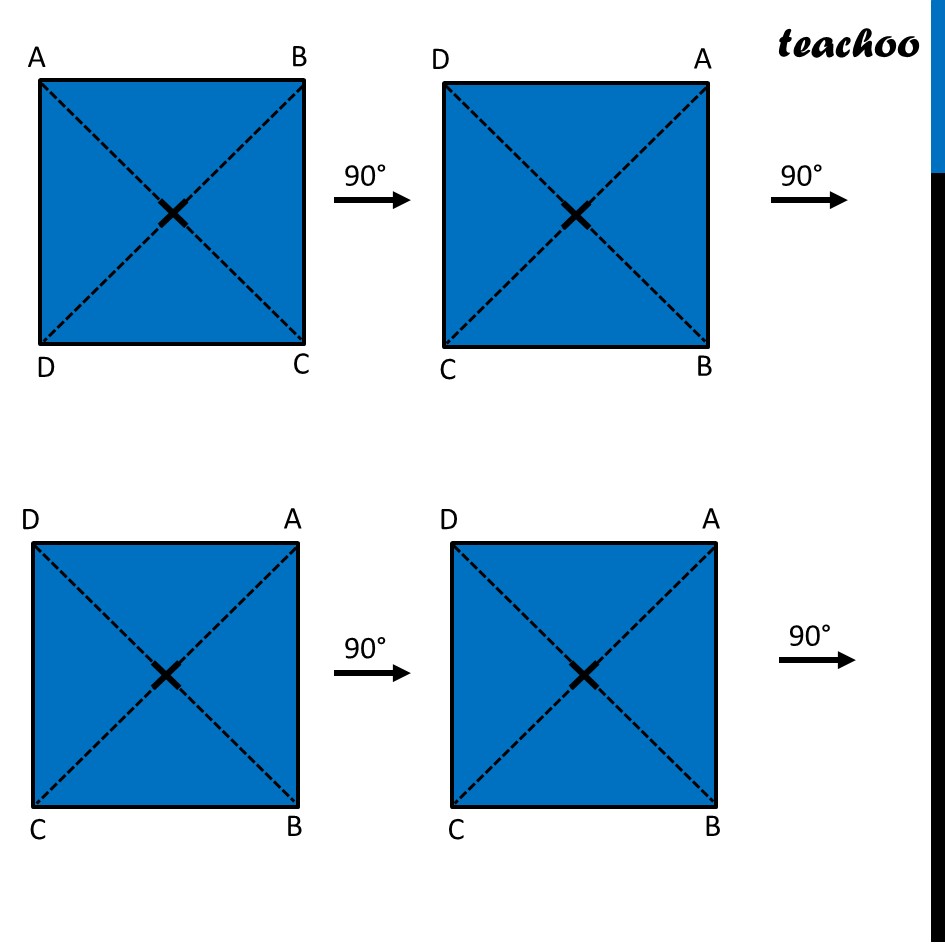
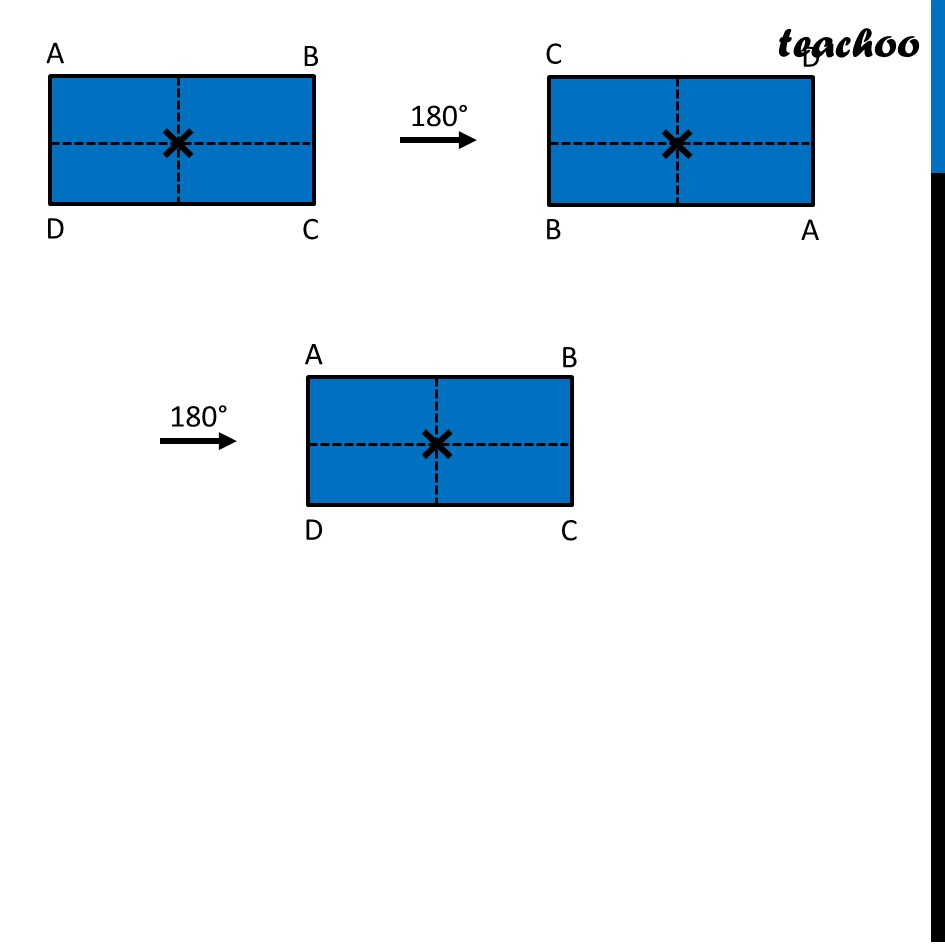
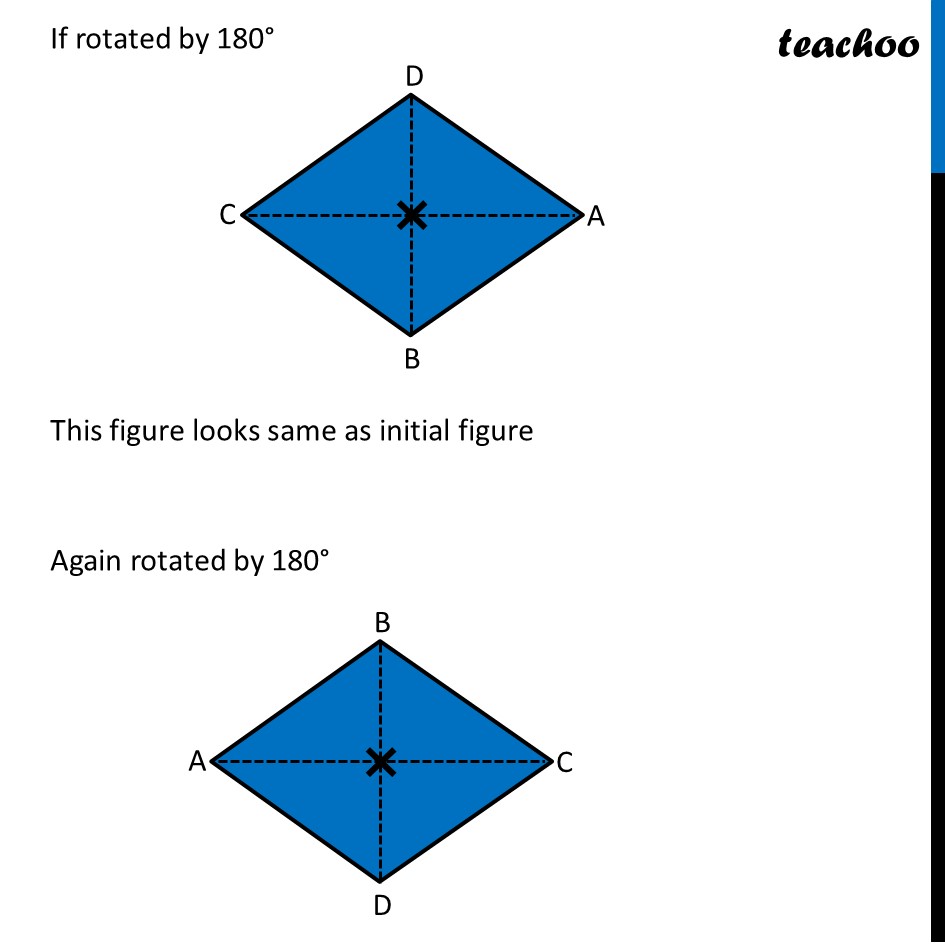
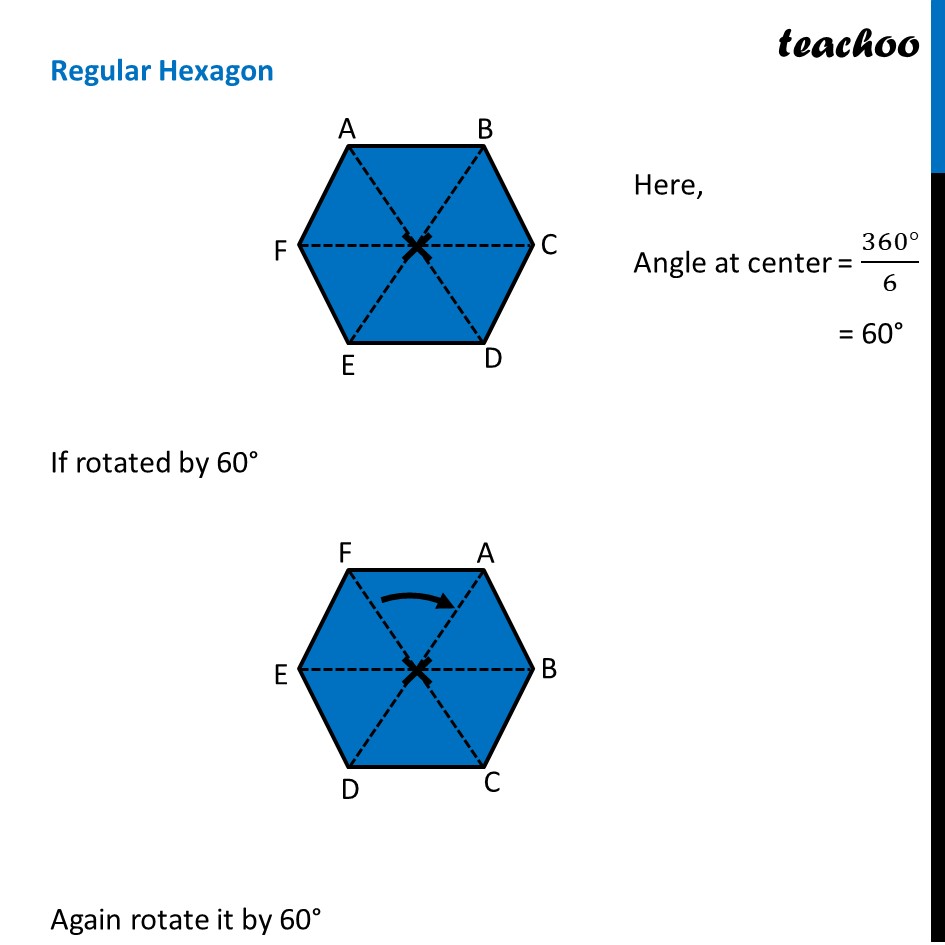
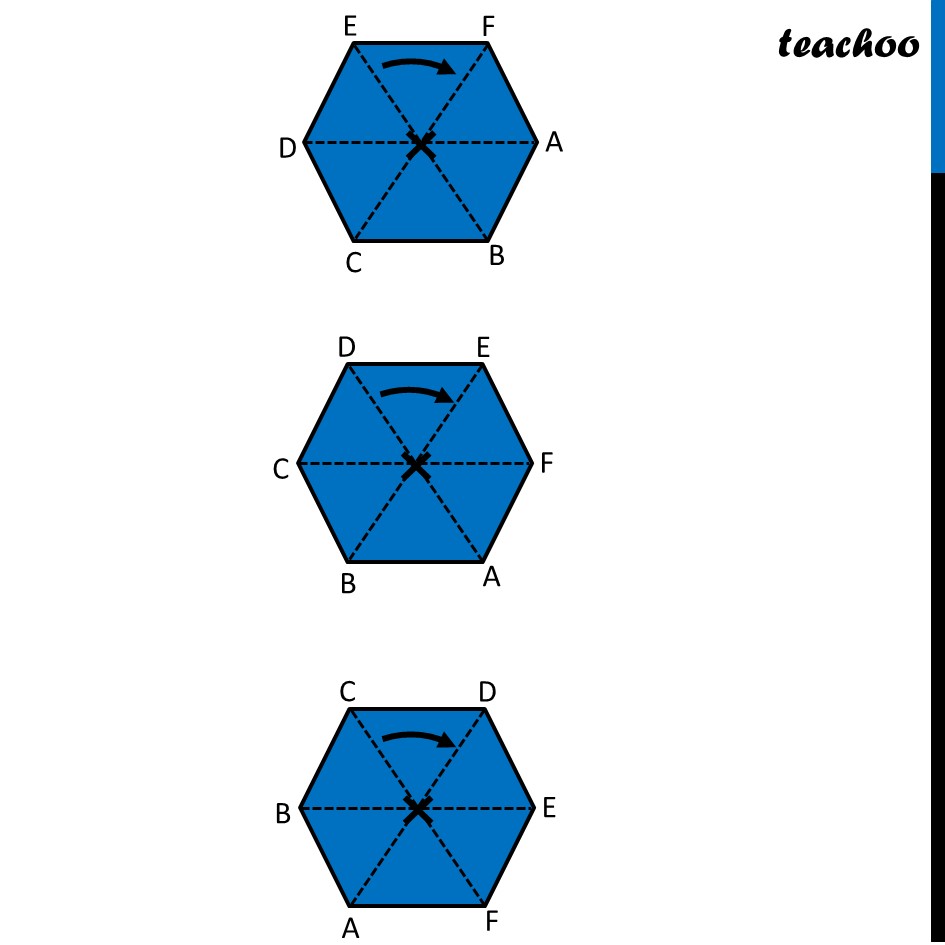
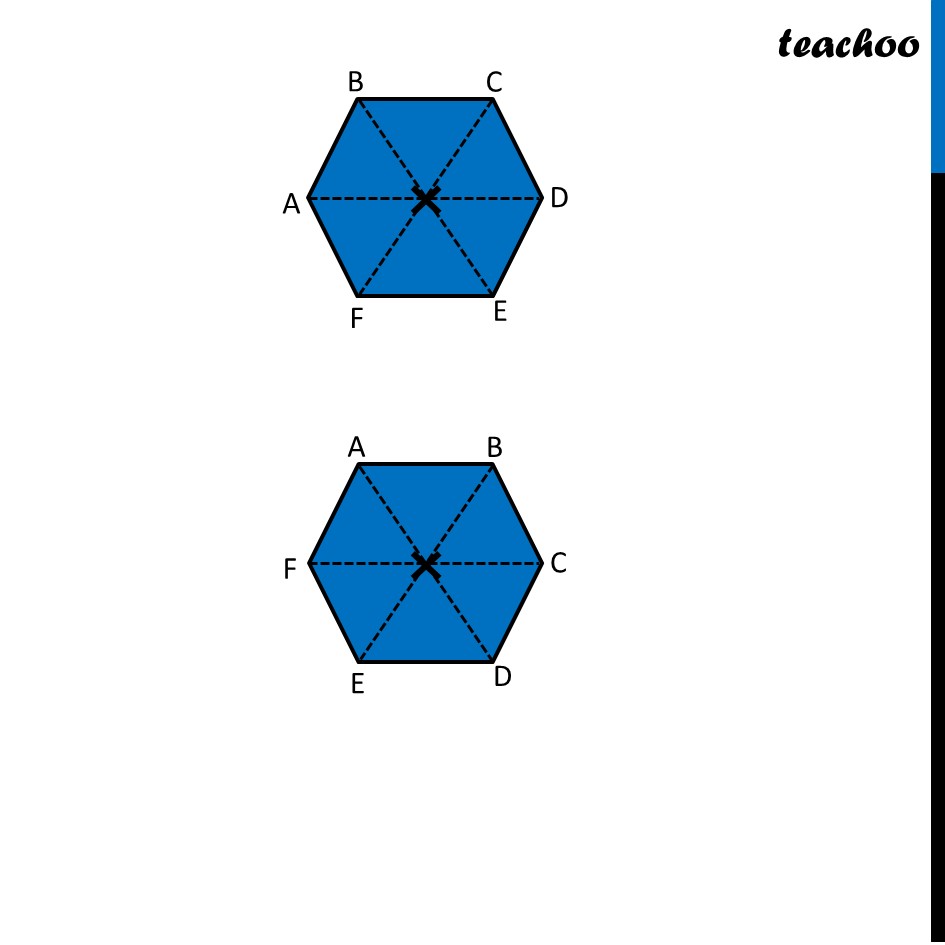
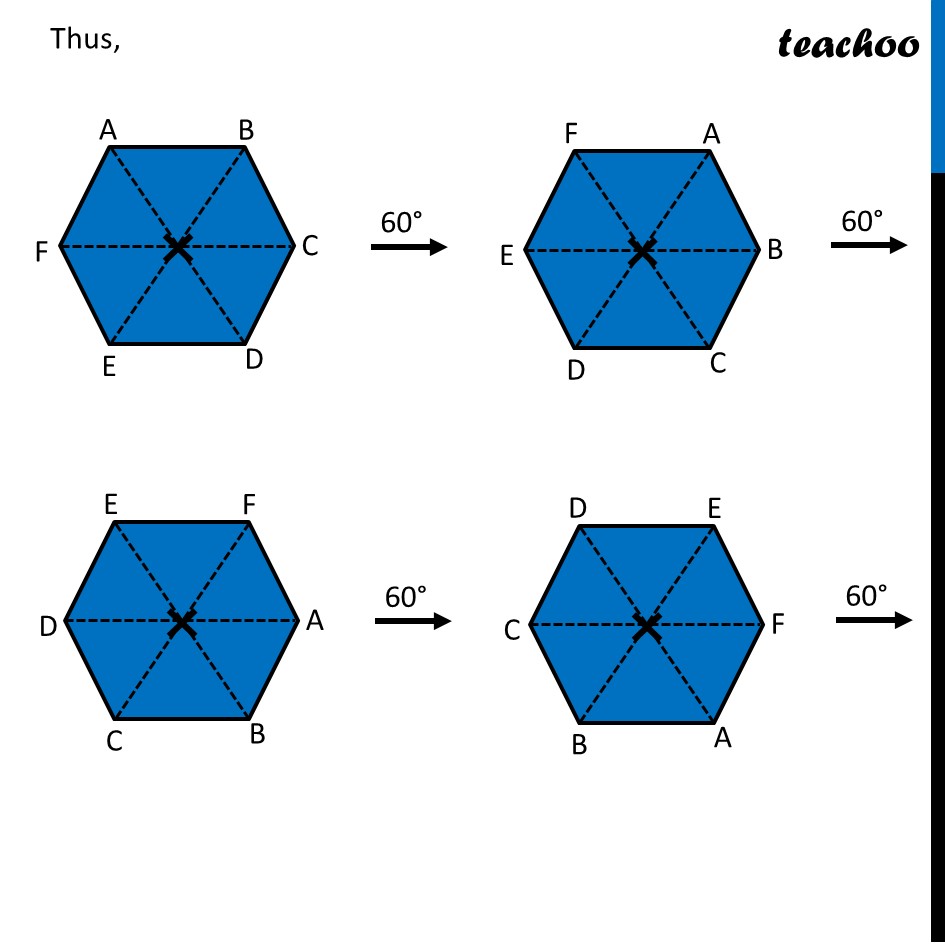
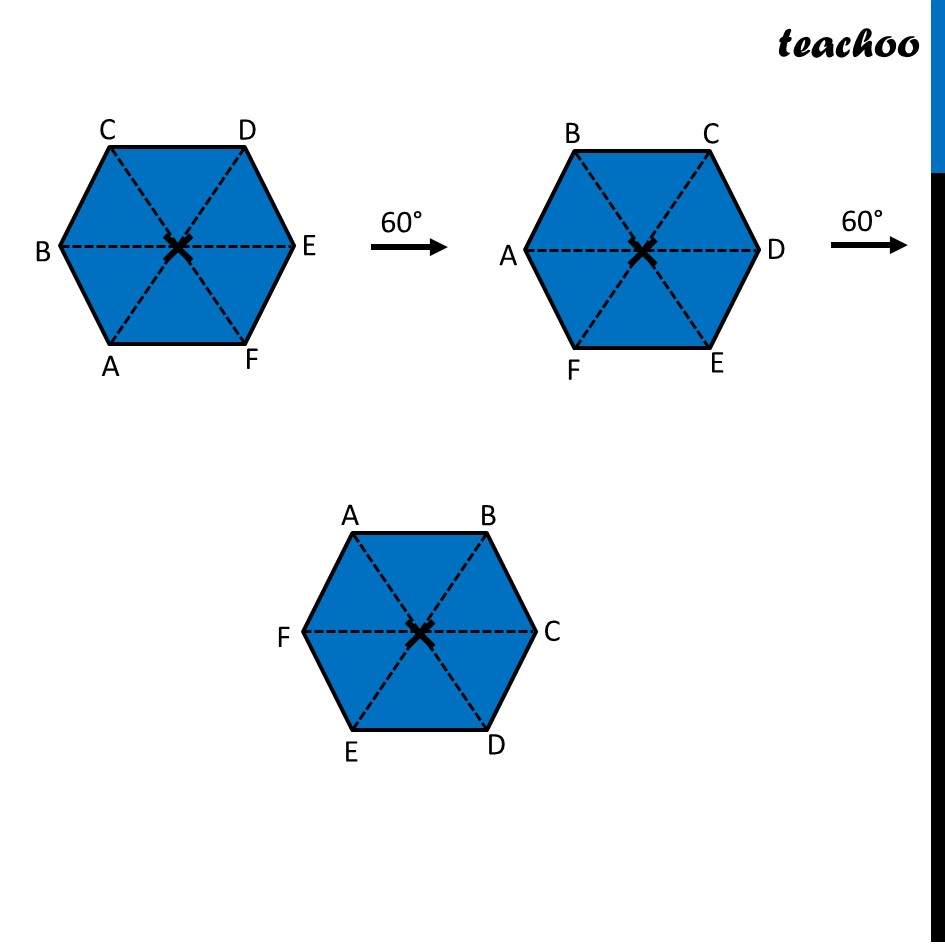
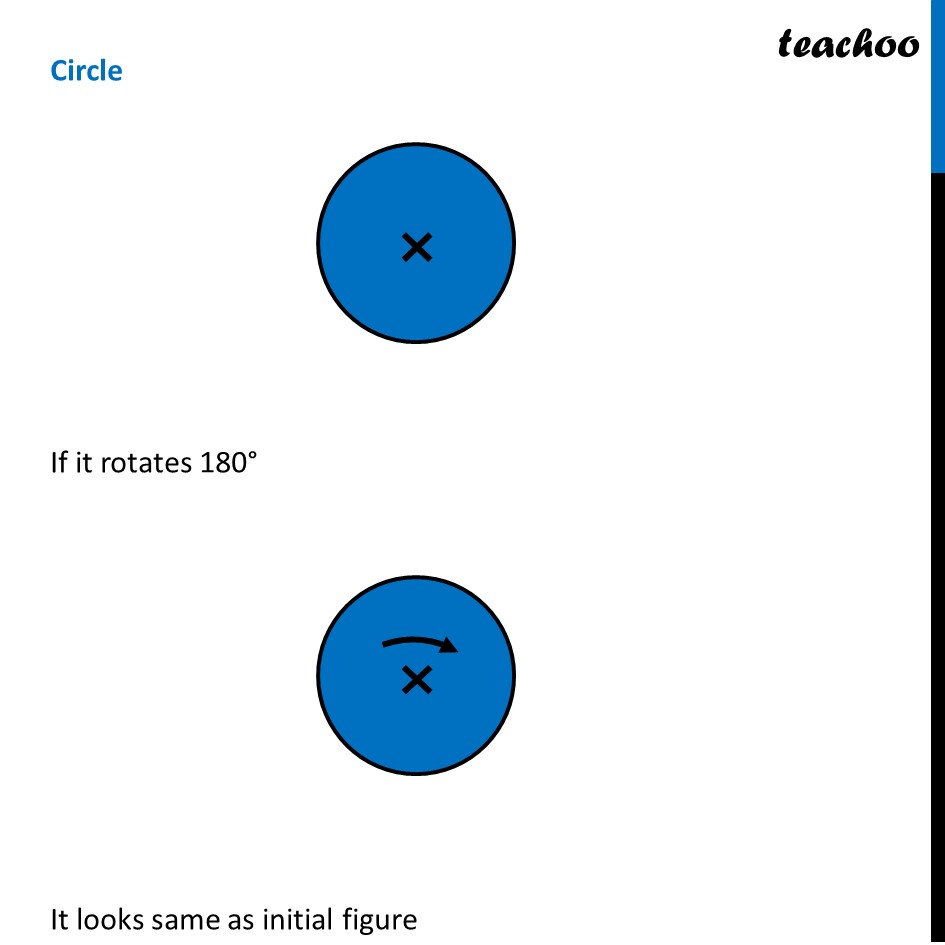
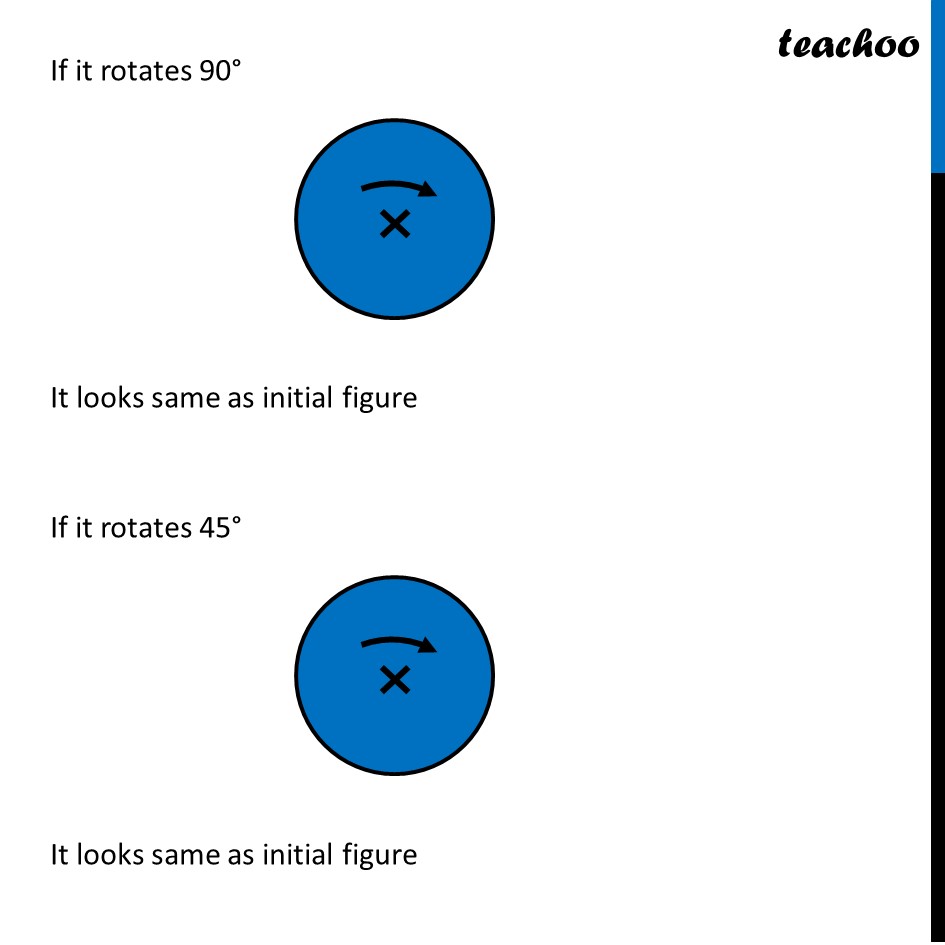
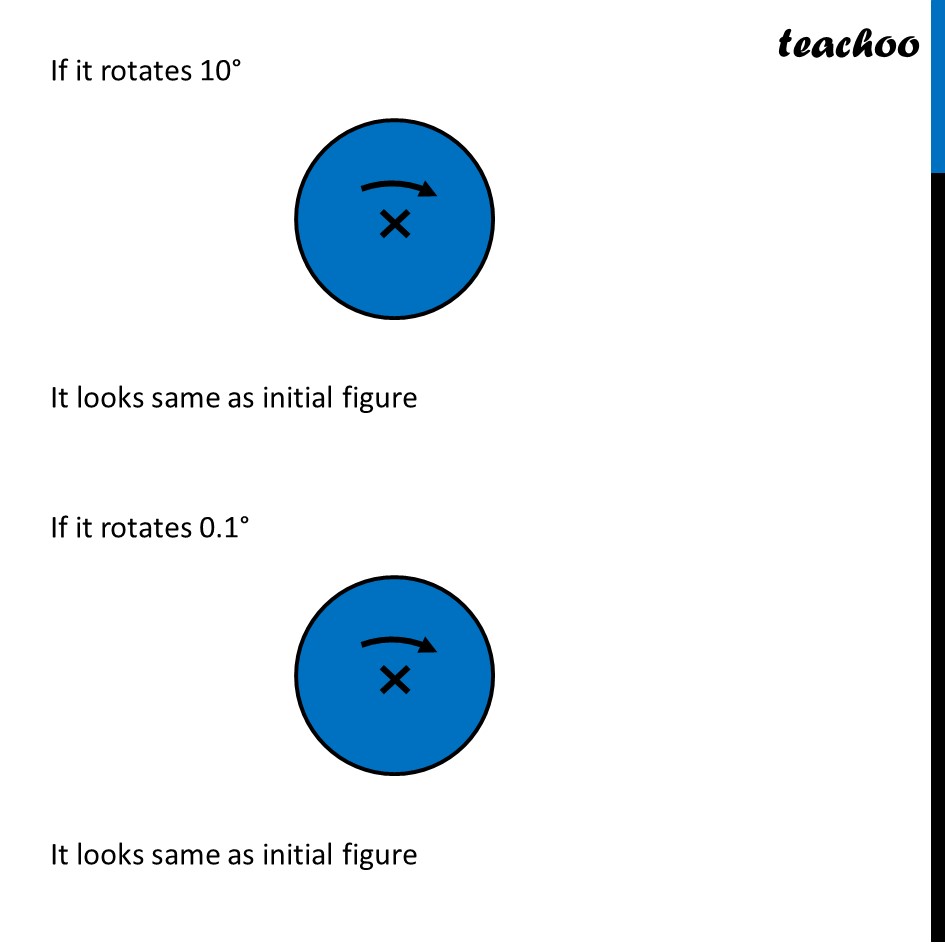
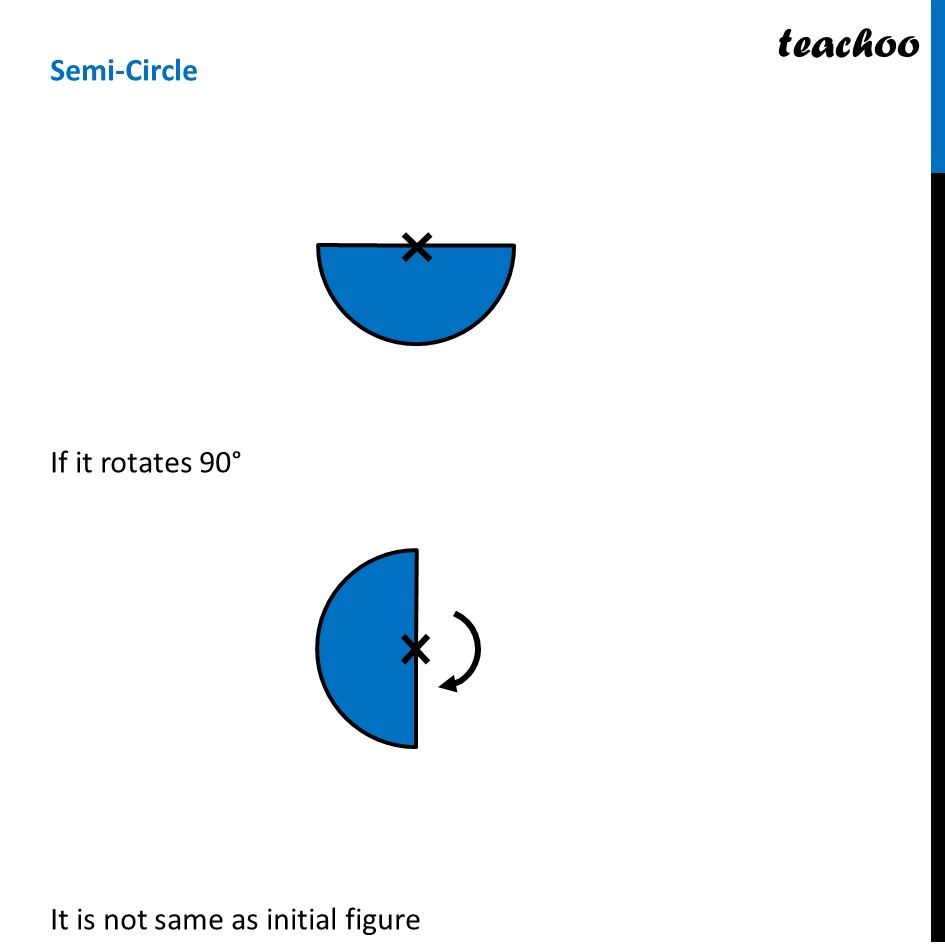
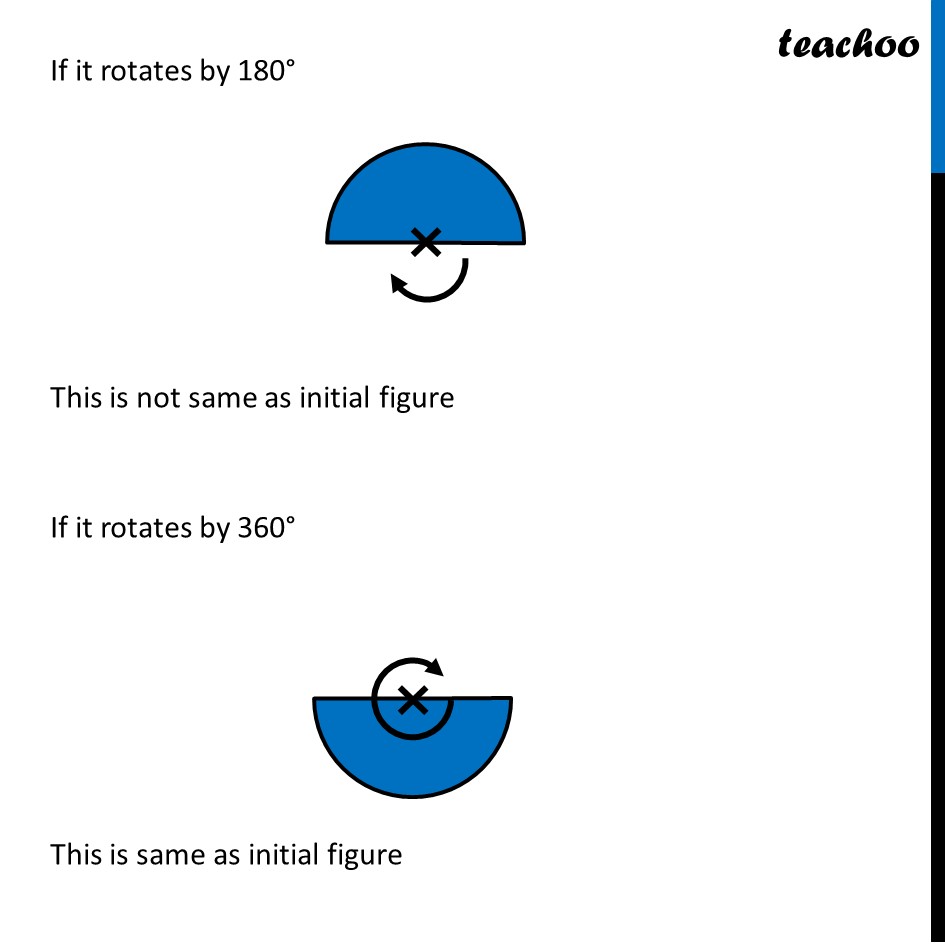
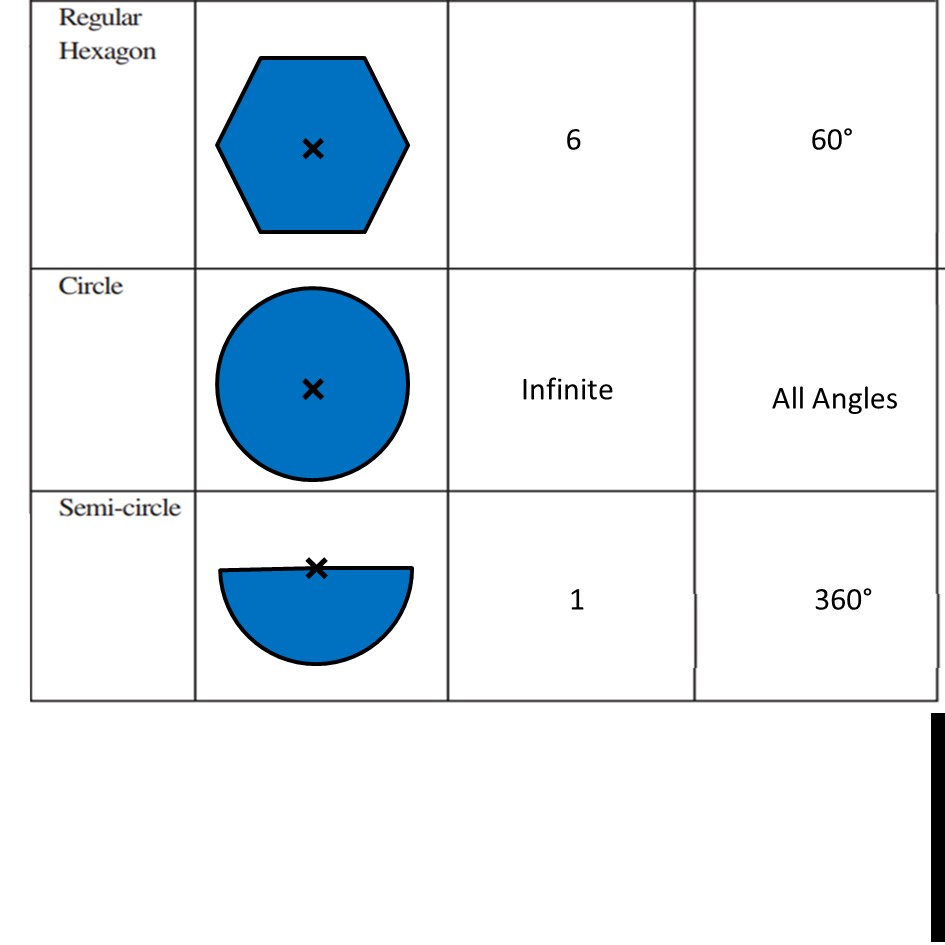
Ex 12.3, 4 Fill in the blanks: (Done before) Square (Done before) Rectangle Rhombus If rotated by 90° This figure is not same as initial figure If rotated by 180° This figure looks same as initial figure Again rotated by 180° Thus, in 1 full – turn (i.e 360°) The figure is same as that of initial 2 turns So, we say that this figure has rotational symmetry of order 2 Regular Hexagon If rotated by 60° Again rotate it by 60° Here, Angle at center = (360°)/6 = 60° Thus, Circle If it rotates 180° It looks same as initial figure If it rotates 90° It looks same as initial figure If it rotates 45° It looks same as initial figure If it rotates 10° It looks same as initial figure If it rotates 0.1° It looks same as initial figure If it rotates 0.01° It looks same as initial figure Therefore, Circle has infinite order of rotational symmetry Semi-Circle If it rotates 90° It is not same as initial figure If it rotates by 180° This is not same as initial figure If it rotates by 360° This is same as initial figure So, this figure on rotation is same as initial figure only when it has rotated 360° So, it has order of rotational symmetry 1