Ex 6.2,8 - Chapter 6 Class 12 Application of Derivatives

Last updated at April 16, 2024 by

Ex 6.2, 8 - Find x for which y = x(x - 2)2 is increasing

Ex 6.2,8 - Chapter 6 Class 12 Application of Derivatives - Part 2
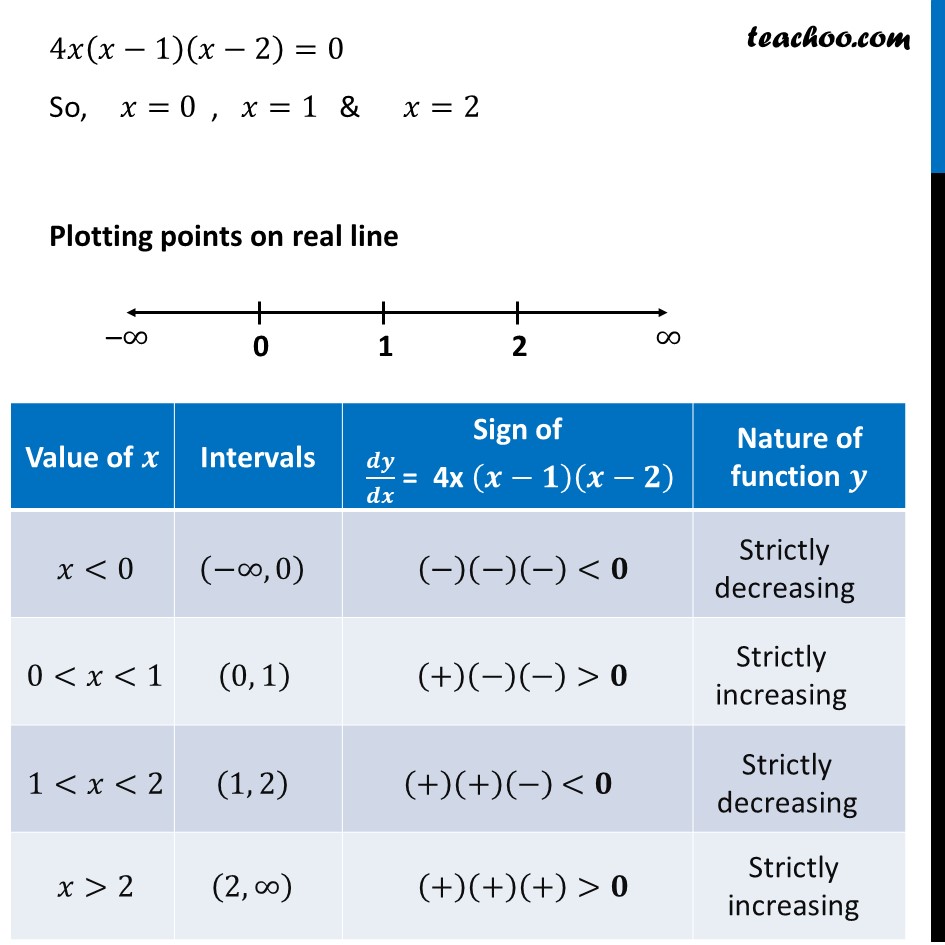
Ex 6.2,8 - Chapter 6 Class 12 Application of Derivatives - Part 3
Ex 6.2,8 - Chapter 6 Class 12 Application of Derivatives - Part 4

Transcript

Ex 6.2, 8 Find the values of 𝑥 for which y = [𝑥(𝑥 – 2)]2 is an increasing function 𝑦 = [𝑥(𝑥−2)]^2 Finding 𝒅𝒚/𝒅𝒙 𝑦 = [𝑥(𝑥−2)]^2 𝑦 = [𝑥^2−2𝑥]^2 𝑦 = (𝑥)^4+(2𝑥)^2−2(𝑥^2 )(2𝑥) 𝒚 = 𝒙^𝟒+𝟒𝒙^𝟐−𝟒𝒙^𝟑 Differentiating w.r.t 𝑥 𝑑𝑦/𝑑𝑥=𝑑(𝑥^4 + 4𝑥^2 − 4𝑥^3 )/𝑑𝑥 𝑑𝑦/𝑑𝑥=4𝑥^3+8𝑥−12𝑥^2 𝑑𝑦/𝑑𝑥=4𝑥(𝑥^2+2−3𝑥) 𝑑𝑦/𝑑𝑥=4𝑥(𝑥^2−3𝑥+2) 𝑑𝑦/𝑑𝑥=4𝑥(𝑥^2−2𝑥−𝑥+2) 𝑑𝑦/𝑑𝑥=4𝑥(𝑥(𝑥−2)−1(𝑥−2)) 𝑑𝑦/𝑑𝑥=4𝑥((𝑥−1)(𝑥−2)) 𝑑𝑦/𝑑𝑥=4𝑥(𝑥−1)(𝑥−2) Putting 𝒅𝒚/𝒅𝒙=𝟎 4𝑥(𝑥−1)(𝑥−2)=0 So, 𝑥=0 , 𝑥=1 & 𝑥=2 Plotting points on real line Thus, the function is strictly increasing for 0 <𝒙<𝟏 and 𝒙>𝟐

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.