








Miscellaneous
Misc 1 (ii) Important
Misc 2 Important
Misc 3 Important
Misc 4 (MCQ)
Misc 5 (MCQ) Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Important Deleted for CBSE Board 2024 Exams
Question 10 Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 12 Deleted for CBSE Board 2024 Exams
Question 13 (MCQ) Deleted for CBSE Board 2024 Exams You are here
Question 14 (MCQ) Important Deleted for CBSE Board 2024 Exams
Miscellaneous
Last updated at April 16, 2024 by Teachoo











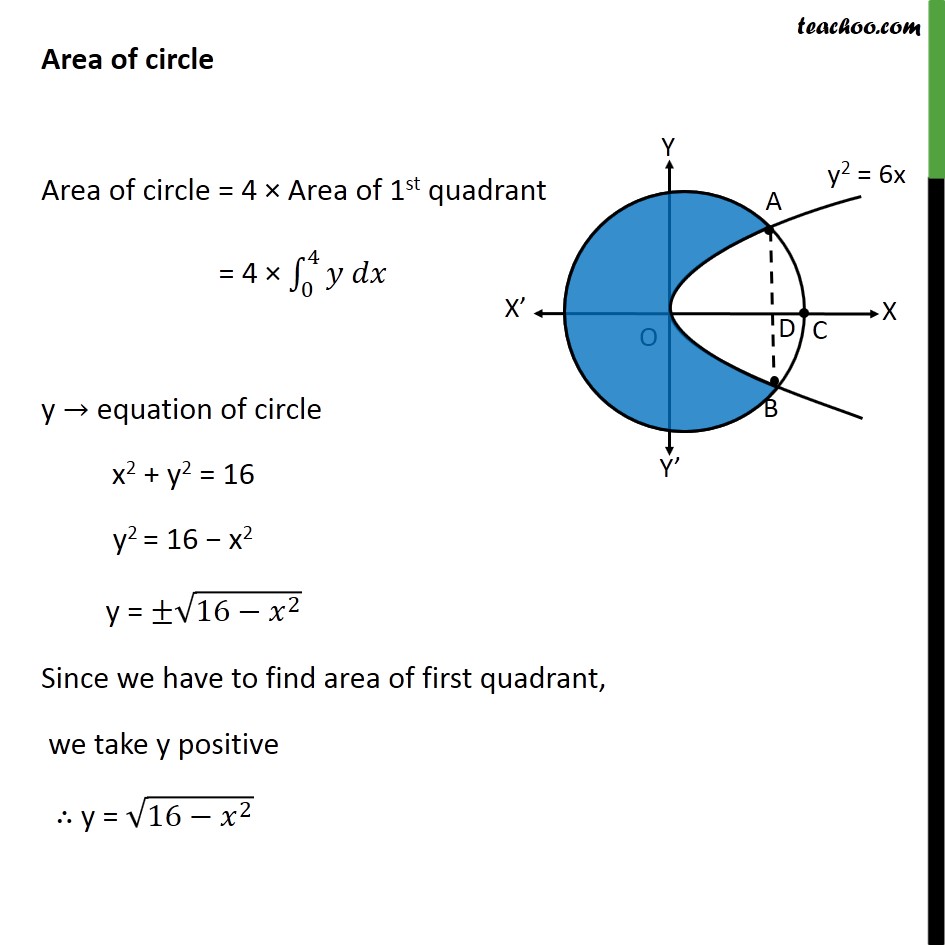
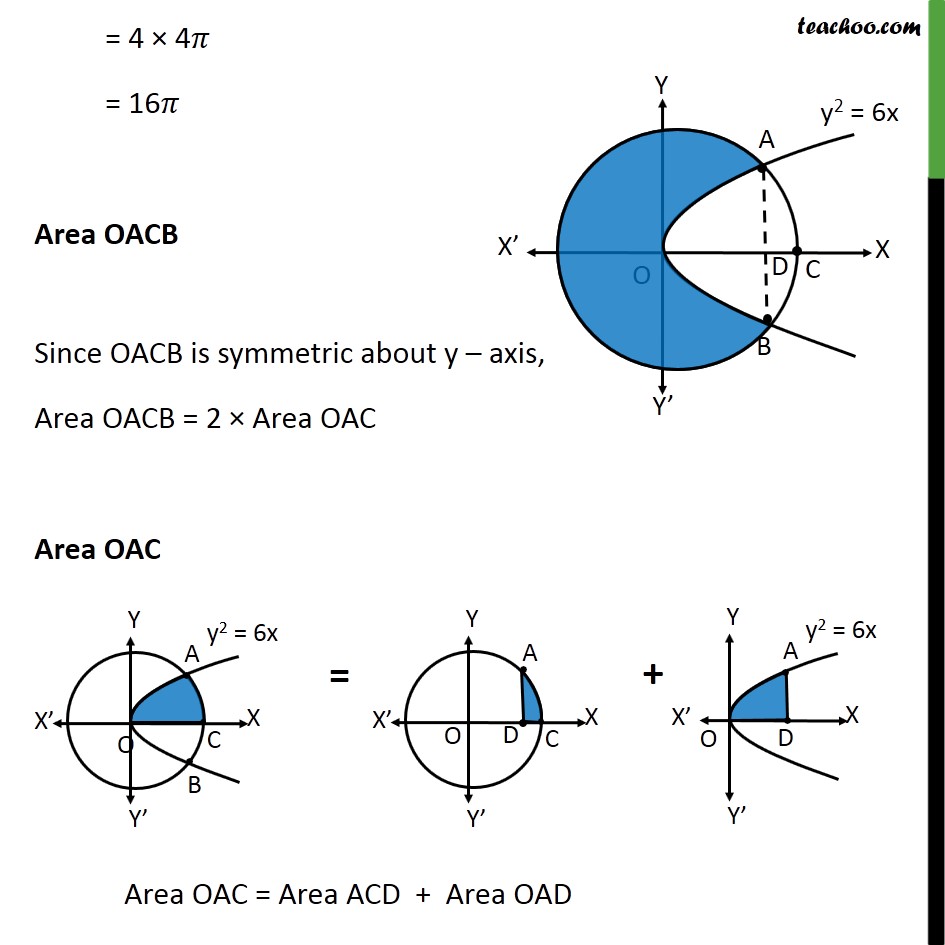
Misc 18 The area of the circle 𝑥2+𝑦2 = 16 exterior to the parabola 𝑦2=6𝑥 is (A) 43 (4𝜋− 3 ) (B) 43 (4𝜋+ 3) (C) 43 (8𝜋− 3) (D) 43 (8𝜋+ 3) Step 1: Draw the Figure 𝑥2+𝑦2 = 16 𝑥2+𝑦2= 42 It is a circle with center 0 , 0 & radius 4 And y2 = 6x is a parabola Step 2: Finding point of intersection A & B Solving 𝑦2=6𝑥 …(1) & 𝑥2+ 𝑦2=16 …(2) Putting (1) in (2) 𝑥2+ 𝑦2=16 𝑥2+6𝑥=16 𝑥2+6𝑥−16=0 𝑥2+8𝑥−2𝑥−16=0 𝑥(𝑥+8) −2(𝑥+8)=0 𝑥−2 𝑥+8=0 So, 𝑥=2 & 𝑥=−8 Area of circle Area of circle = 4 × Area of 1st quadrant = 4 × 04𝑦 𝑑𝑥 y → equation of circle x2 + y2 = 16 y2 = 16 − x2 y = ± 16− 𝑥2 Since we have to find area of first quadrant, we take y positive ∴ y = 16− 𝑥2 Therefore Area of circle = 4 × 04 16− 𝑥2𝑑𝑥 = 4 × 04 42− 𝑥2𝑑𝑥 = 4 × 𝑥2 42− 𝑥2+ 422 sin−1 𝑥404 = 4 × 𝑥2 16− 𝑥2+8 sin−1 𝑥404 = 4 × 42 16− 42+8 sin−1 44− 02 16− 02+8 sin−1 04 = 4 × 0+8 sin−11−0−8 sin−10 = 4 × 0+8× 𝜋2−0−0 = 4 × 4𝜋 = 16𝜋 Area OACB Since OACB is symmetric about y – axis, Area OACB = 2 × Area OAC Area OAC Area ACD Area ACD = 24𝑦 𝑑𝑥 y → equation of circle x2 + y2 = 16 y2 = 16 − x2 y = ± 16 − x2 Since ACD is 1st quadrant y = 16− 𝑥2 Therefore, Area ACD = 24 16− 𝑥2 𝑑𝑥 = 24 42− 𝑥2 = 24 42− 𝑥2 = 𝑥2 42− 𝑥2+ 424 sin−1 𝑥424 = 𝑥2 16− 𝑥2+8 sin−1 𝑥424 = 42 16− 42+8 sin−1 44 − 22 16− 22+8 sin−1 24 = 8 × 𝜋2 − 2 3 − 8 × 𝜋6 = 4𝜋 − 4𝜋3 − 2 3 = 8𝜋3 − 2 3 Area OAD Area OAD = 02𝑦 𝑑𝑥 y → equation of parabola y2 = 6x y = 6𝑥 Therefore, Area OAD = 02 6𝑥 𝑑𝑥 = 6 02 𝑥 12 𝑑𝑥 = 6 × 𝑥 32 3202 = 2 63 2 32− 0 32 = 2 63 × 2 2 = 4 2× 3× 23 = 8 33 Area OAC = Area ACD + Area OAD = 8𝜋3−2 3+ 83 3 = 8𝜋3+ 23 3 Thus, Area OACB = 2 × Area OAC = 2 × 8𝜋3+ 2 33 = 16𝜋3+ 4 33 Therefore, Required Area = Area of circle − Area OACB = 16𝜋 − 4 33+ 163𝜋 = 32𝜋3− 4 33 = 43(8𝜋 − 3) square units. So, C is the correct answer