

Miscellaneous
Misc 1 (ii) Important
Misc 2 Important
Misc 3 Important
Misc 4 (MCQ)
Misc 5 (MCQ) Important You are here
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Important Deleted for CBSE Board 2024 Exams
Question 10 Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 12 Deleted for CBSE Board 2024 Exams
Question 13 (MCQ) Deleted for CBSE Board 2024 Exams
Question 14 (MCQ) Important Deleted for CBSE Board 2024 Exams
Miscellaneous
Last updated at April 16, 2024 by Teachoo




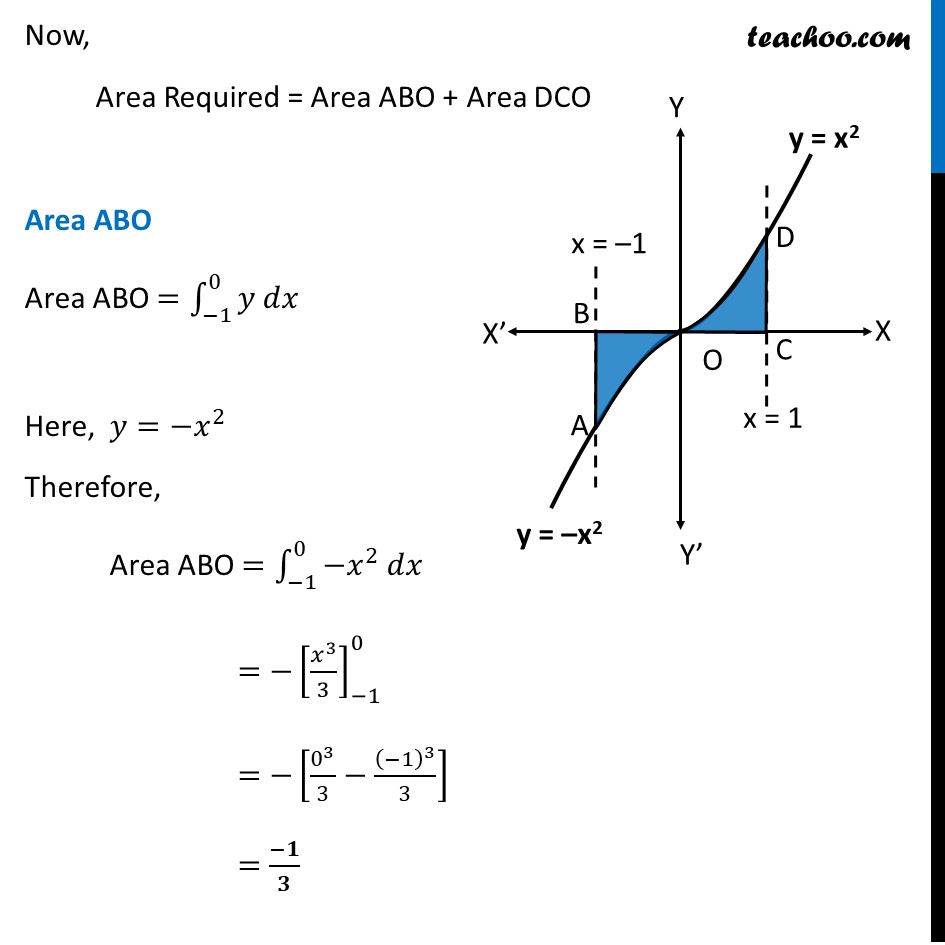
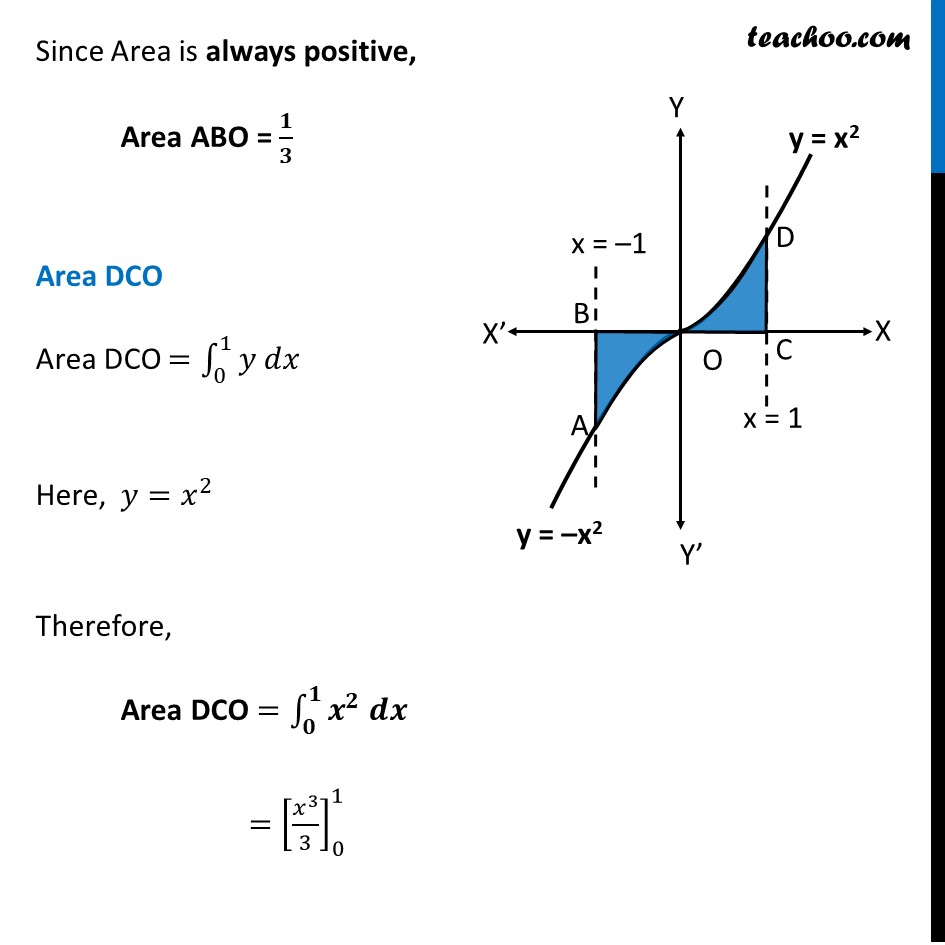
Misc 5 The area bounded by the curve 𝑦 = 𝑥 |𝑥| , 𝑥−𝑎𝑥𝑖𝑠 and the ordinates 𝑥 = – 1 and 𝑥=1 is given by (A) 0 (B) 1/3 (C) 2/3 (D) 4/3 [Hint : 𝑦=𝑥2 if 𝑥 > 0 𝑎𝑛𝑑 𝑦 =−𝑥2 if 𝑥 < 0]We know that |𝑥|={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ Therefore, y = x|𝒙|={█(𝒙𝒙, 𝒙≥𝟎@&𝒙(−𝒙), 𝒙<𝟎)┤ y ={█(𝑥^2, 𝑥≥0@&−𝑥^2, 𝑥<0)┤ Now, Area Required = Area ABO + Area DCO Area ABO Area ABO =∫_(−1)^0▒〖𝑦 𝑑𝑥〗 Here, 𝑦=〖−𝑥〗^2 Therefore, Area ABO =∫_(−1)^0▒〖〖−𝑥〗^2 𝑑𝑥〗 〖=−[𝑥^3/3]〗_(−1)^0 =−[0^3/3−(−1)^3/3] =(−𝟏)/𝟑 Since Area is always positive, Area ABO = 𝟏/𝟑 Area DCO Area DCO =∫_0^1▒〖𝑦 𝑑𝑥〗 Here, 𝑦=𝑥^2 Therefore, Area DCO =∫_𝟎^𝟏▒〖𝒙^𝟐 𝒅𝒙〗 〖=[𝑥^3/3]〗_0^1 =1/3 [1^3−0^3 ] =1/3 [1−0] =𝟏/𝟑 Therefore, Required Area = Area ABO + Area DCO =1/3+1/3 =𝟐/𝟑 square units So, the correct answer is (c)