
Miscellaneous
Misc 1 (ii) Important
Misc 2 Important
Misc 3 Important
Misc 4 (MCQ)
Misc 5 (MCQ) Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams You are here
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Important Deleted for CBSE Board 2024 Exams
Question 10 Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 12 Deleted for CBSE Board 2024 Exams
Question 13 (MCQ) Deleted for CBSE Board 2024 Exams
Question 14 (MCQ) Important Deleted for CBSE Board 2024 Exams
Miscellaneous
Last updated at April 16, 2024 by Teachoo





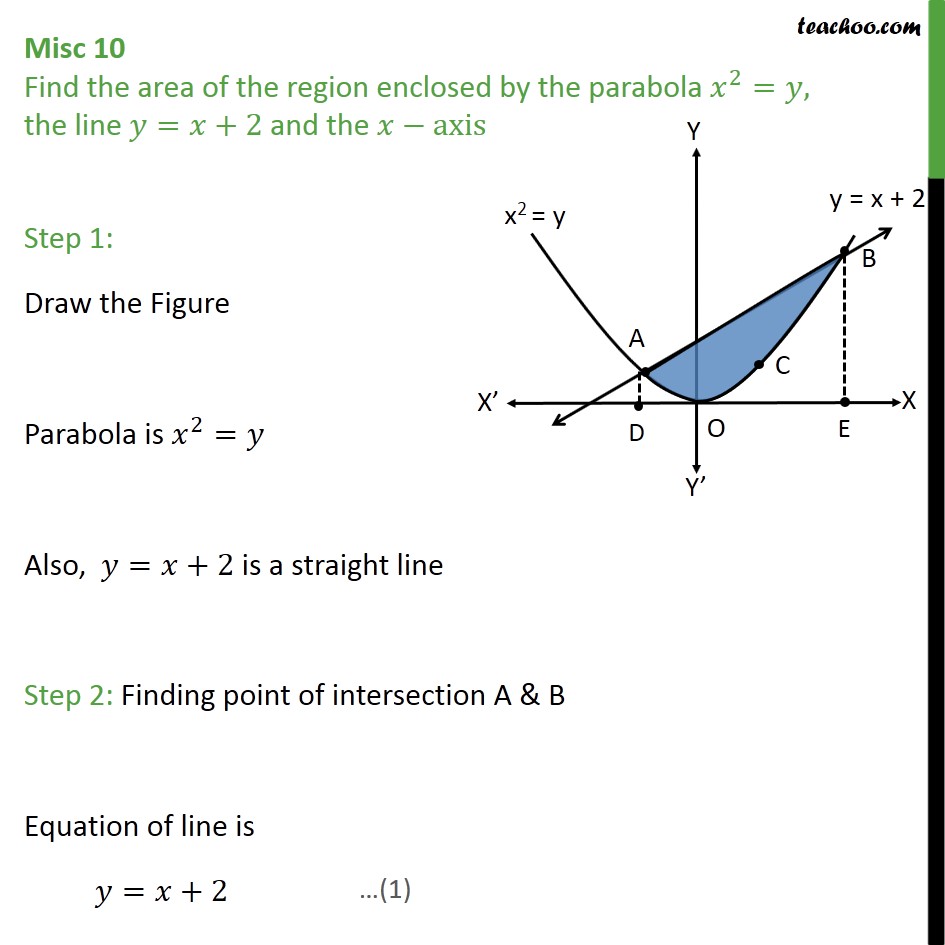
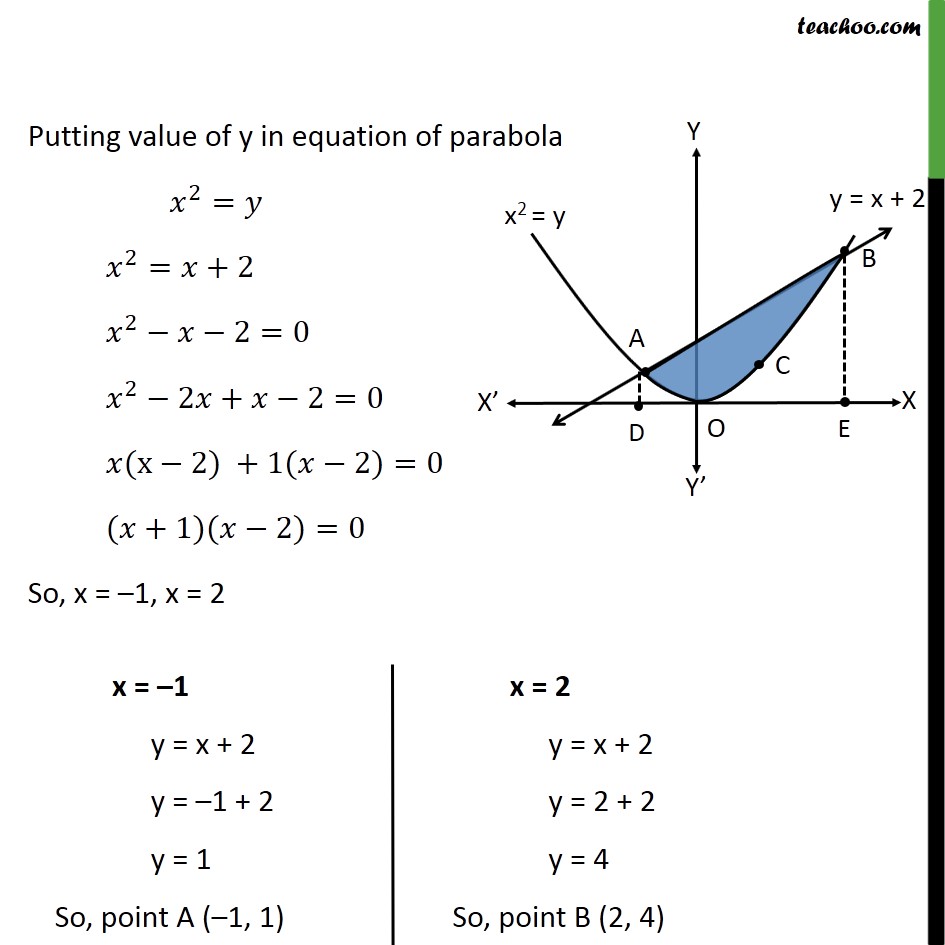
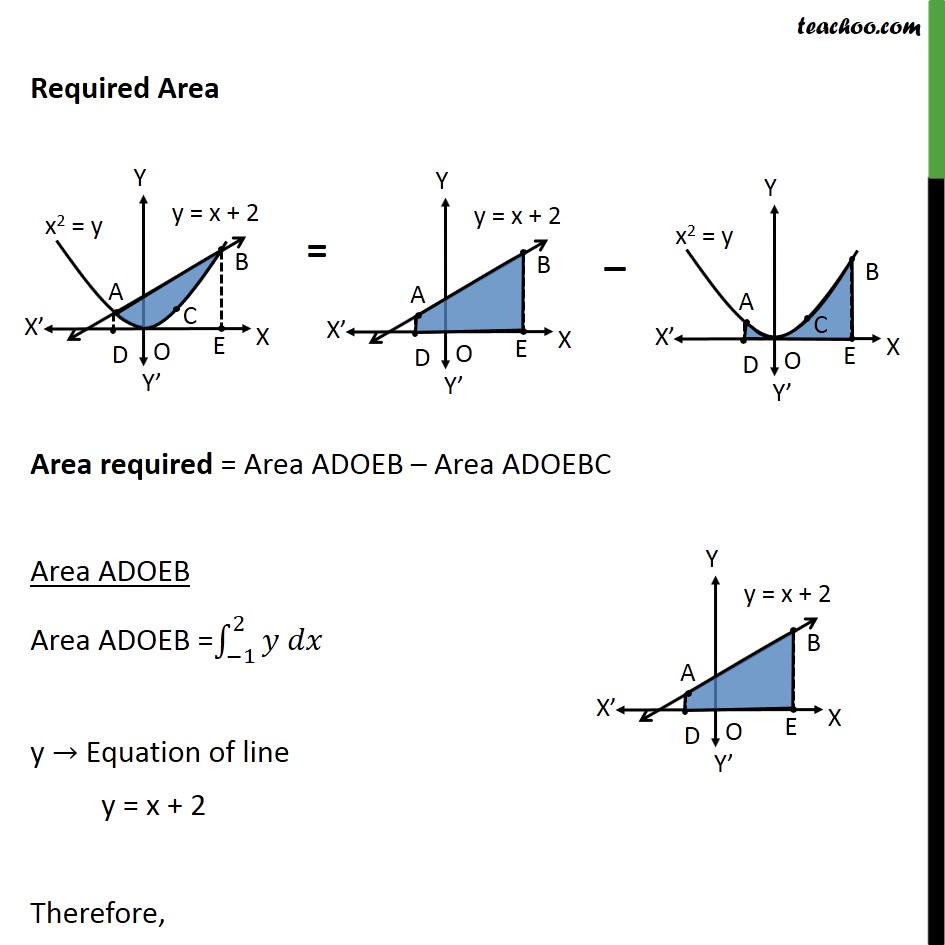
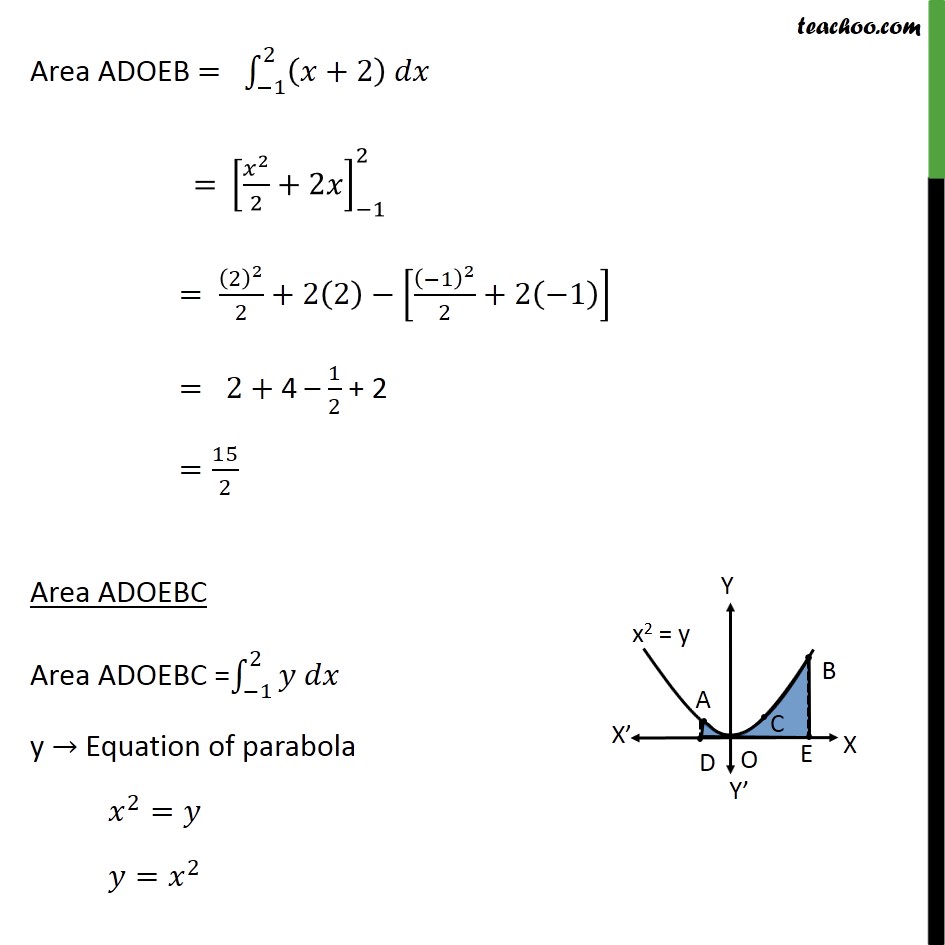
Question 7 Find the area of the region enclosed by the parabola 𝑥2=𝑦, the line 𝑦=𝑥+2 and the 𝑥−axis Step 1: Draw the Figure Parabola is 𝑥2=𝑦 Also, 𝑦=𝑥+2 is a straight line Step 2: Finding point of intersection A & B Equation of line is 𝑦=𝑥+2 Putting value of y in equation of parabola 𝑥2=𝑦 𝑥2=𝑥+2 𝑥2−𝑥−2=0 𝑥2−2𝑥+𝑥−2=0 𝑥(x−2) +1(𝑥−2)=0 (𝑥+1)(𝑥−2)=0 So, x = –1, x = 2 Required Area Area required = Area ADOEB – Area ADOEBC Area ADOEB Area ADOEB = −12𝑦 𝑑𝑥 y → Equation of line y = x + 2 Therefore, Area ADOEB = −12 𝑥+2 𝑑𝑥 = 𝑥22+2𝑥−12 = 222+2 2− −122+2 −1 = 2+ 4 – 12 + 2 = 152 Area ADOEBC Area ADOEBC = −12𝑦 𝑑𝑥 y → Equation of parabola 𝑥2=𝑦 𝑦= 𝑥2 Therefore, Area ADOEBC = −12 𝑥2 𝑑𝑥 = 𝑥33−12 = 13 23− −13 = 93 = 3 Area required = Area ADOEB – Area ADOEBC = 152 – 3 = 92