


Examples
Example 2 Important
Example 3
Example 4 Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams You are here
Question 4 Important Deleted for CBSE Board 2024 Exams
Question 5 Important Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Deleted for CBSE Board 2024 Exams
Question 10 Important Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Last updated at April 16, 2024 by Teachoo




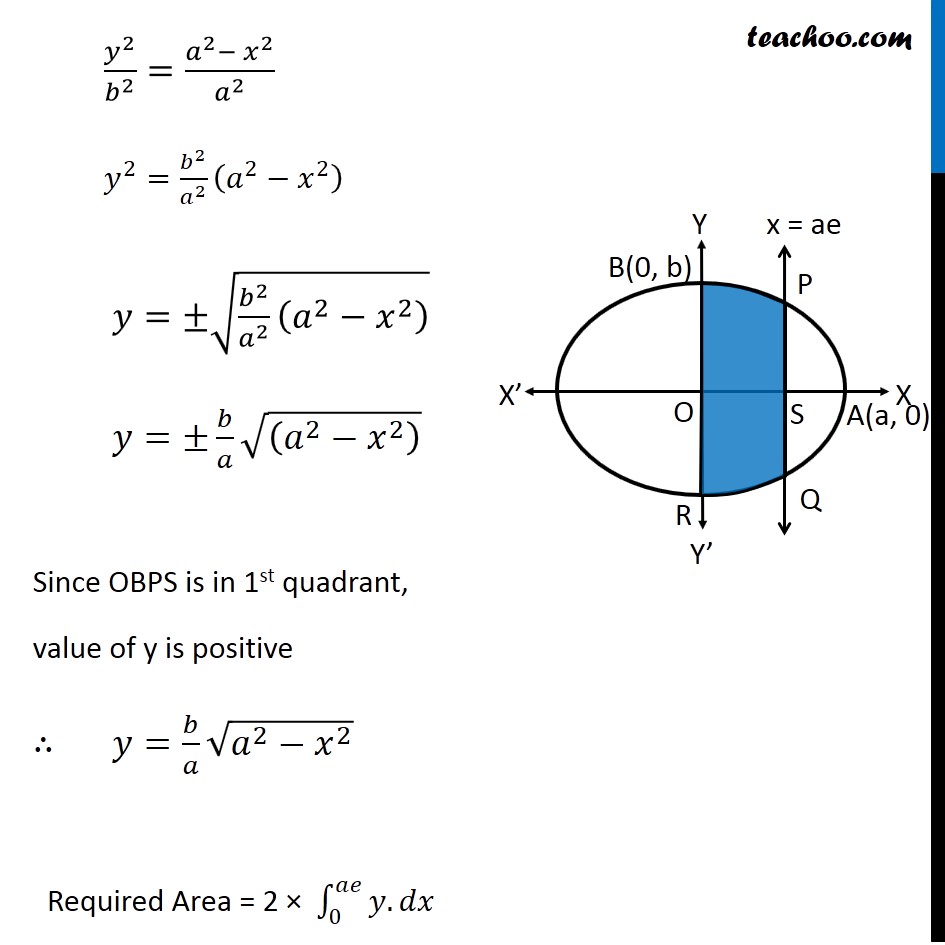
Question 3 Find the area bounded by the ellipse 𝑥^2/𝑎^2 +𝑦^2/𝑏^2 =1 and the ordinates 𝑥=0 and 𝑥=𝑎𝑒, where, 𝑏2=𝑎2 (1 – 𝑒2) and e < 1 Required Area = Area of shaded region = Area BORQSP = 2 × Area OBPS = 2 × ∫_0^𝑎𝑒▒〖𝑦.𝑑𝑥〗 We know that , 𝑥^2/𝑎^2 +𝑦^2/𝑏^2 =1 (As ellipse is symmetric about its axis ) 𝑦^2/𝑏^2 =(𝑎^2−〖 𝑥〗^2)/𝑎^2 𝑦^2=𝑏^2/𝑎^2 (𝑎^2−𝑥^2 ) 𝑦=±√(𝑏^2/𝑎^2 (𝑎^2−𝑥^2 ) ) 𝑦=±𝑏/𝑎 √((𝑎^2−𝑥^2 ) ) Since OBPS is in 1st quadrant, value of y is positive ∴ 𝑦=𝑏/𝑎 √(𝑎^2−𝑥^2 ) Required Area = 2 × ∫_0^𝑎𝑒▒〖𝑦.𝑑𝑥〗 = 2∫_0^𝑎𝑒▒〖𝑏/𝑎 √(𝑎^2−𝑥^2 )〗 𝑑𝑥 = 2𝑏/𝑎 ∫_0^𝑎𝑒▒√(𝑎^2−𝑥^2 ) 𝑑𝑥 = 2𝑏/𝑎 [1/2 𝑥√(𝑎^2−𝑥^2 )+𝑎^2/2 sin^(−1)〖𝑥/𝑎〗 ]_0^𝑎𝑒 =2𝑏/𝑎 [(𝑎𝑒/2 √(𝑎^2−(𝑎𝑒)^2 )+𝑎^2/2 sin^(−1)〖𝑎𝑒/𝑎〗 )−(0/2 √(𝑎^2−0)+𝑎^2/2 sin^(−1)(0/𝑎) )] =2𝑏/𝑎 [𝑎𝑒/2 √(𝑎^2−𝑎^2 𝑒^2 )+𝑎^2/2 sin^(−1)〖(𝑒)−0−𝑎^2/2 sin^(−1)(0) 〗 ] =2𝑏/𝑎 [𝑎𝑒/2.𝑎√(1−𝑒^2 )+𝑎^2/2 sin^(−1)〖𝑒−0〗 ] It is of form √(𝑎^2−𝑥^2 ) 𝑑𝑥=1/2 𝑥√(𝑎^2−𝑥^2 )+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)〖 𝑥/𝑎+𝑐〗 =2𝑏/𝑎 [(𝑎^2 𝑒)/2 √(1−𝑒^2 )+𝑎^2/2 sin^(−1)𝑒 ] =2𝑏/𝑎 (𝑎^2/2)[𝑒√(1−𝑒^2 )+sin^(−1)𝑒 ] =𝑎𝑏[𝑒√(1−𝑒^2 )+sin^(−1)𝑒 ] ∴ Required Area =𝒂𝒃[𝒆√(𝟏−𝒆^𝟐 )+〖𝒔𝒊𝒏〗^(−𝟏)𝒆 ] square units