

Examples
Example 2 Important
Example 3
Example 4 Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Important Deleted for CBSE Board 2024 Exams
Question 5 Important Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams
Question 9 Deleted for CBSE Board 2024 Exams
Question 10 Important Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Last updated at April 16, 2024 by Teachoo



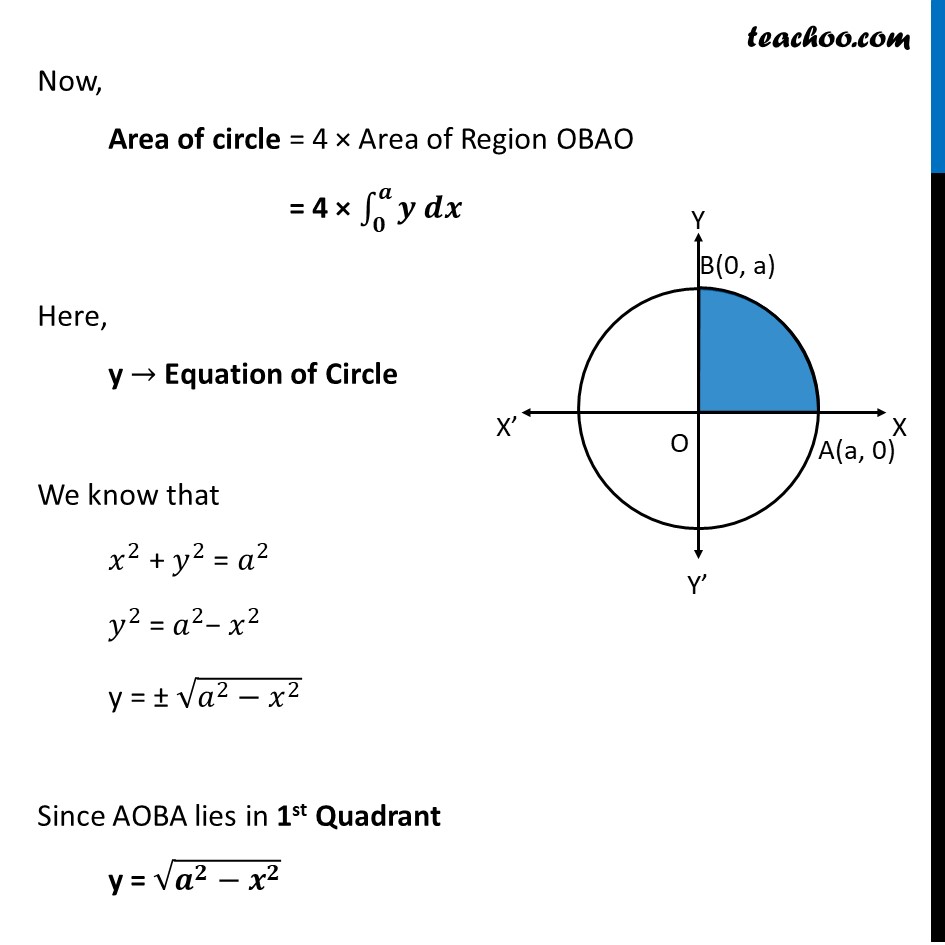
Example 1 Find the area enclosed by the circle 𝑥2 + 𝑦2 = 𝑎2Given 𝑥^2 + 𝑦^2= 𝑎^2 This is a circle with Center = (0, 0) Radius = 𝑎 Since radius is a, OA = OB = 𝑎 A = (𝑎, 0) B = (0, 𝑎) Now, Area of circle = 4 × Area of Region OBAO = 4 × ∫1_𝟎^𝒂▒〖𝒚 𝒅𝒙〗 Here, y → Equation of Circle We know that 𝑥^2 + 𝑦^2 = 𝑎^2 𝑦^2 = 𝑎^2− 𝑥^2 y = ± √(𝑎^2−𝑥^2 ) Since AOBA lies in 1st Quadrant y = √(𝒂^𝟐−𝒙^𝟐 ) Now, Area of circle = 4 × ∫1_0^𝑎▒〖𝑦 𝑑𝑥〗 = 4 × ∫1_0^𝑎▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥〗 Using: √(𝑎^2−𝑥^2 )dx = 1/2 √(𝑎^2−𝑥^2 ) + 𝑎^2/2 〖"sin" 〗^(−1) 𝑥/4 + c = 4[𝒙/𝟐 √(𝒂^𝟐−𝒙^𝟐 )+𝒂^𝟐/𝟐 〖"sin" 〗^(−𝟏) 𝒙/𝒂]_𝟎^𝒂 = 4[𝑎/2 √(𝑎^2−𝑎^2 )+𝑎^2/2 〖"sin" 〗^(−1) 𝑎/𝑎−0/2 √(𝑎^2−0)−0^2/2 〖"sin" 〗^(−1) (0)] = 4[0+𝑎^2/2 〖"sin" 〗^(−1) (1)−0−0] = 4.𝑎^2/2. 𝜋/2 = 𝝅𝒂^𝟐