Question 1 - Area between 2 curves - Chapter 8 Class 12 Application of Integrals

Transcript

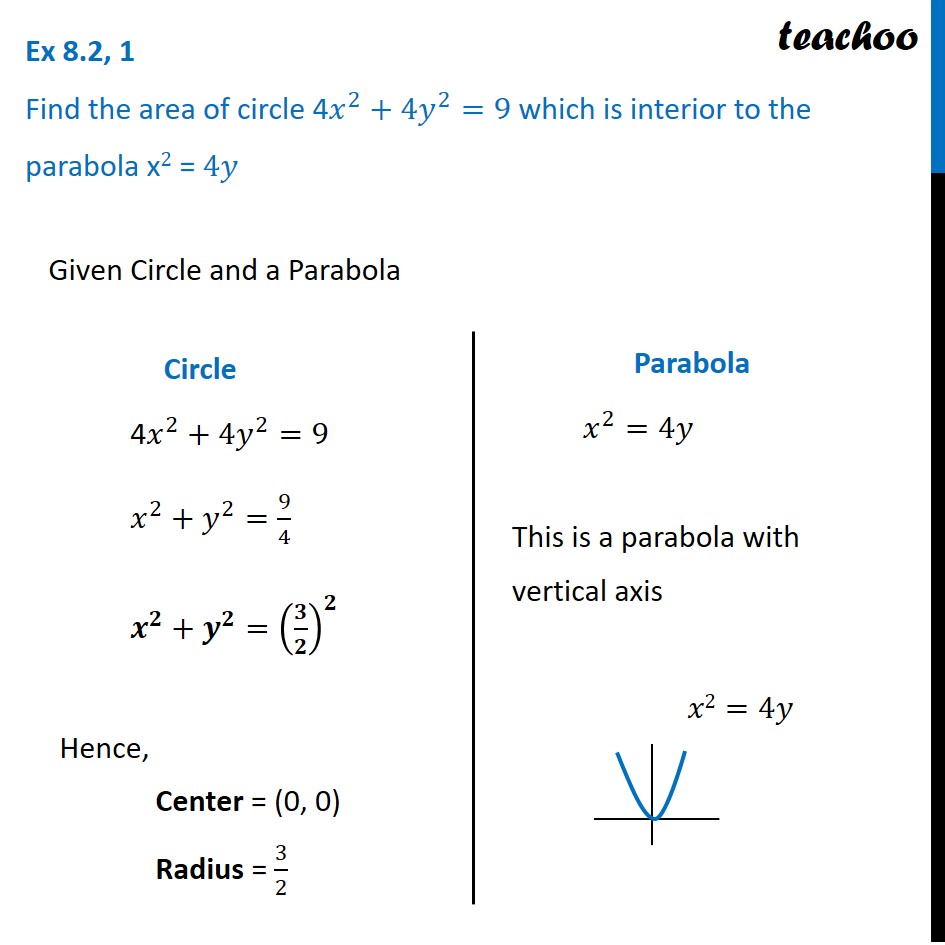
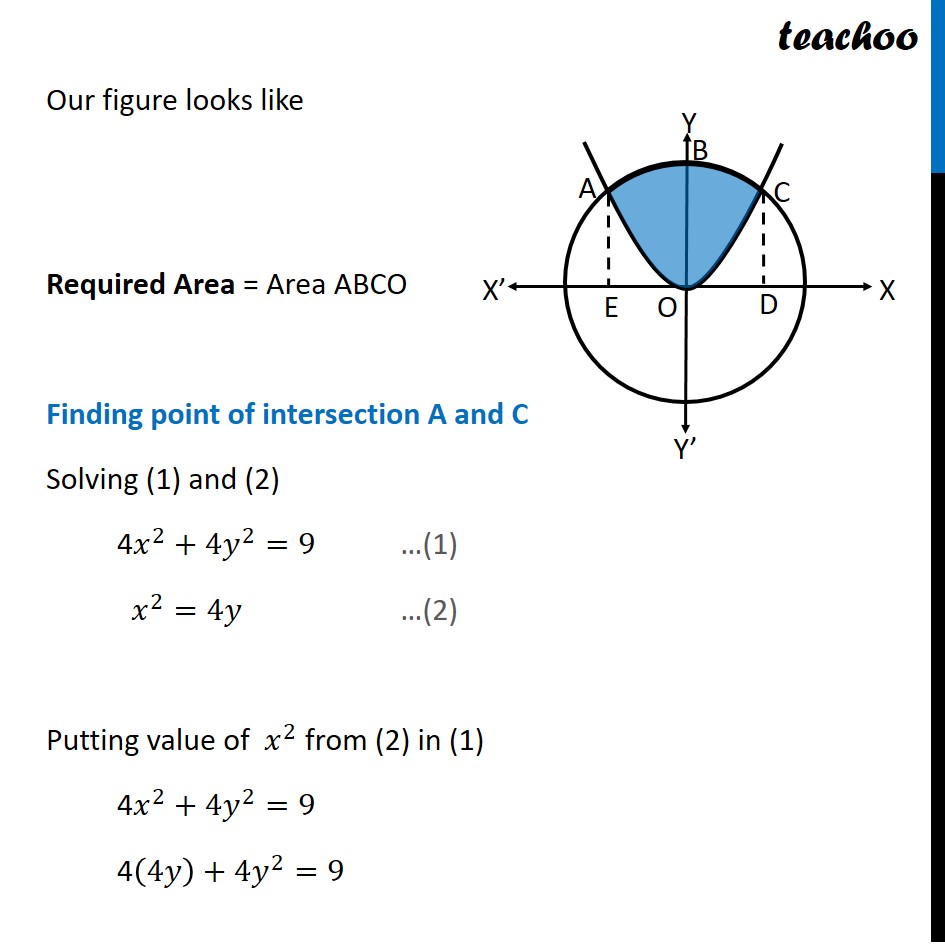
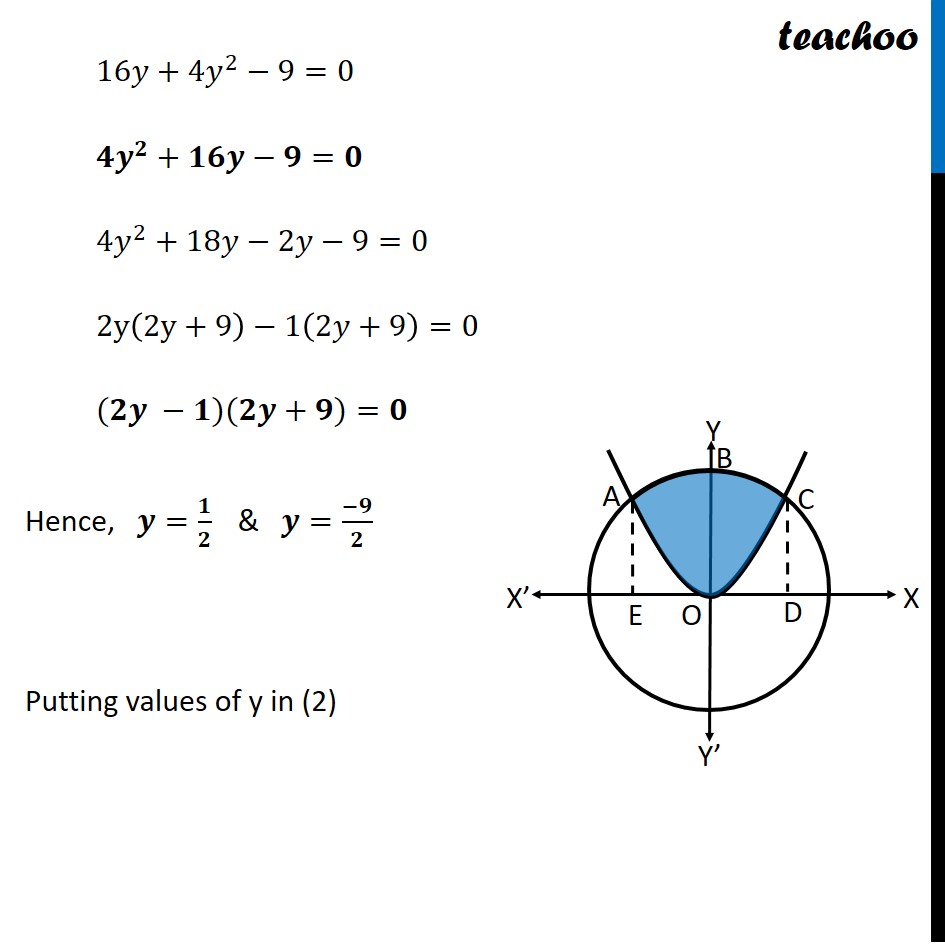
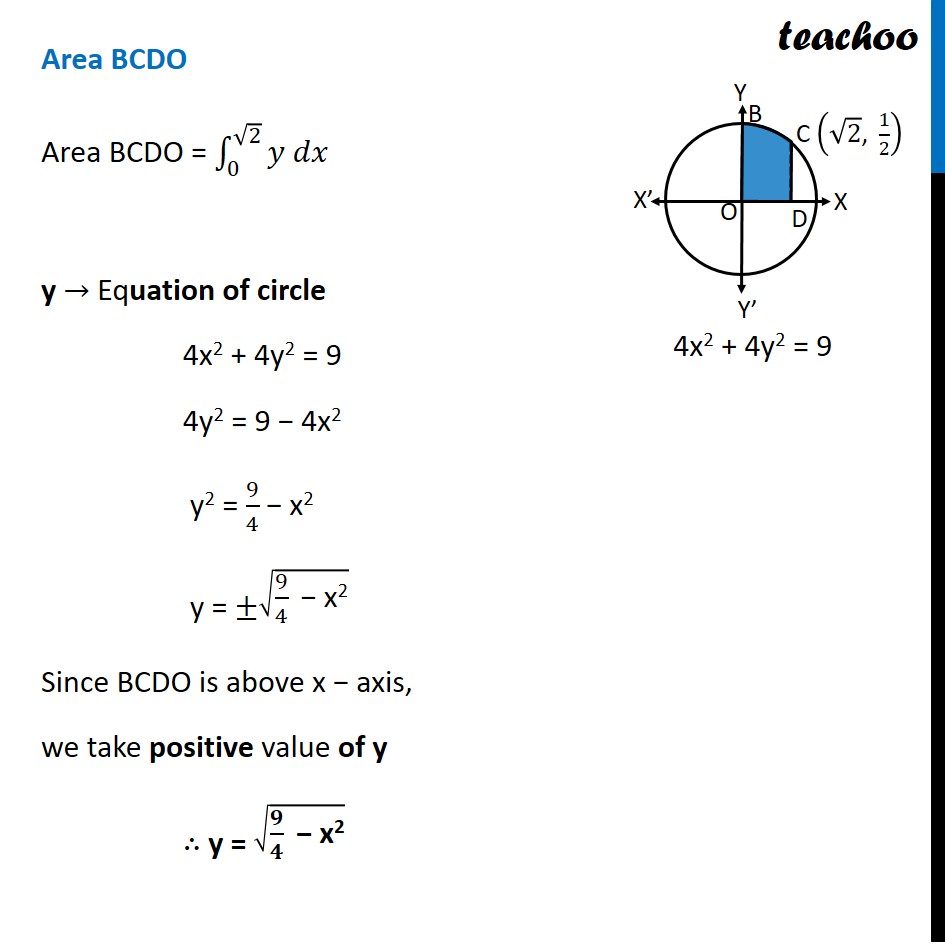
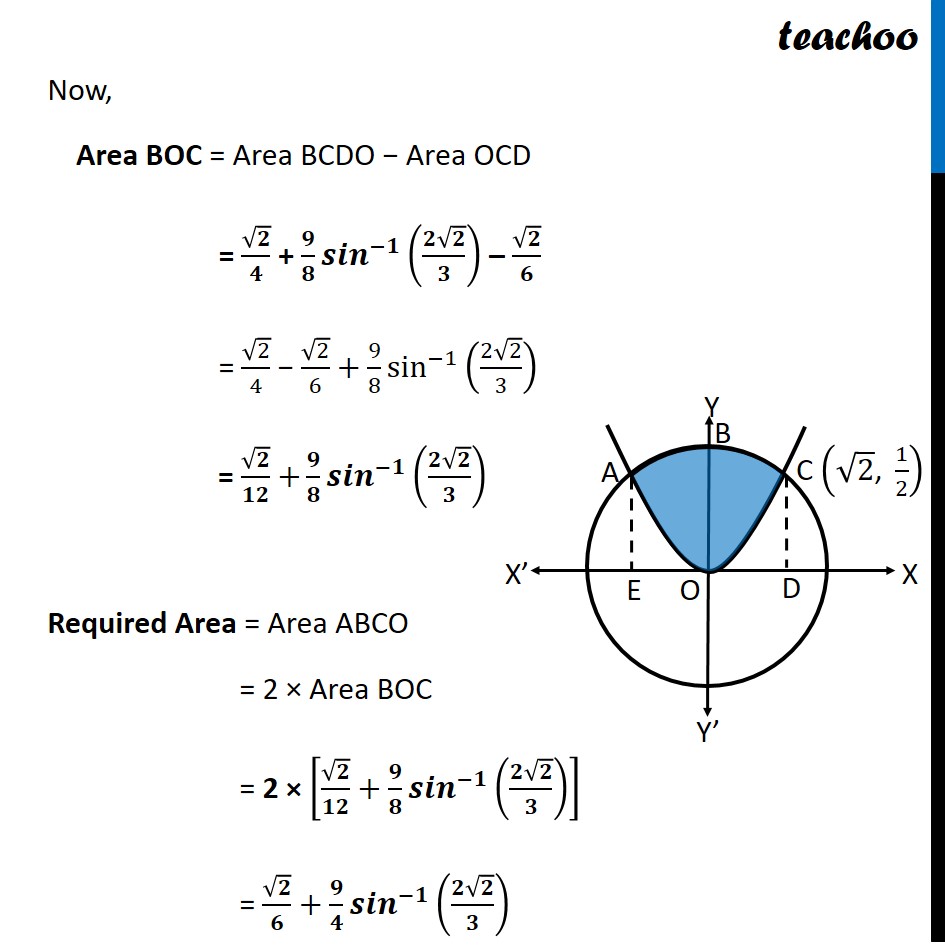
Question 1 Find the area of circle 4𝑥^2+4𝑦^2=9 which is interior to the parabola x2 = 4𝑦 Given Circle and a Parabola Circle 4𝑥^2+4𝑦^2=9 𝑥^2+𝑦^2=9/4 𝒙^𝟐+𝒚^𝟐=(𝟑/𝟐)^𝟐 Hence, Center = (0, 0) Radius = 3/2 Parabola 𝑥^2=4𝑦 This is a parabola with vertical axis Our figure looks like Required Area = Area ABCO Finding point of intersection A and C Solving (1) and (2) 4𝑥^2+4𝑦^2=9 …(1) 𝑥^2=4𝑦 …(2) Putting value of 𝑥^2 from (2) in (1) 4𝑥^2+4𝑦^2=9 4(4𝑦)+4𝑦^2=9 16𝑦+4𝑦^2−9=0 〖𝟒𝒚〗^𝟐+𝟏𝟔𝒚−𝟗=𝟎 〖4𝑦〗^2+18𝑦−2𝑦−9=0 2y(2y+9)−1(2𝑦+9)=0 (𝟐𝒚 −𝟏)(𝟐𝒚+𝟗)=𝟎 Hence, 𝒚=𝟏/𝟐 & 𝒚=(−𝟗)/𝟐 Putting values of y in (2) For 𝒚=𝟏/𝟐 𝑥^2=4𝑦 𝑥^2=4 × 1/2 𝑥^2=2 𝒙=±√𝟐 Hence, 𝑥 "= " √2 & 𝑥" ="−√2 For 𝒚=(−𝟗)/𝟐 𝑥^2=4𝑦 𝑥^2=4 ×((−9)/( 2)) 𝑥^2=−2 ×9 𝑥^2=−18 As square cannot be negative, x has no real value Hence the points are A=(−√𝟐 , 𝟏/𝟐) & C=(√𝟐 , 𝟏/𝟐) Finding Area Area required = Area ABCO Since ABCO is symmetric in y – axis, Area ABCO = 2 × Area BOC Area BOC = Area BCDO − Area OCD Area BCDO Area BCDO = ∫_0^(√2)▒〖𝑦 𝑑𝑥〗 y → Equation of circle 4x2 + 4y2 = 9 4y2 = 9 − 4x2 y2 = 9/4 − x2 y = ±√(9/4 " − x2" ) Since BCDO is above x − axis, we take positive value of y ∴ y = √(𝟗/𝟒 " − x2" ) Area BCDO = ∫_𝟎^(√𝟐)▒√(𝟗/𝟒 " − x2" ) dx = ∫_0^(√2)▒√((3/2)^2 " − " "x" ^2 ) dx = [𝒙/𝟐 √((𝟑/𝟐)^𝟐 " − " "x" ^𝟐 )+(𝟑/𝟐)^𝟐/𝟐 〖𝒔𝒊𝒏〗^(−𝟏)⁡〖𝒙/((𝟑/𝟐) )〗 ]_𝟎^√𝟐 = [𝑥/2 √((3/2)^2 " − " "x" ^2 )+9/8 sin^(−1)⁡〖2𝑥/3〗 ]_0^√2 = [√2/2 √(9/4 " − " 〖"(" √2 ")" 〗^2 ) + 9/8 sin^(−1)⁡((2√2)/3) ] − [0/2 √(9/4 " − " "0" ^2 )+9/8 sin^(−1)⁡((2×0)/3) ] We know that ∫1▒〖√(𝑎^2−𝑥^2 ) 𝑑𝑥〗 =𝑥/2 √(𝑎^2−𝑥^2 )+𝑎^2/2 〖𝑠𝑖𝑛〗^(−1)⁡〖𝑥/𝑎+𝑐〗 Putting a = 3/2 = √2/2 √(9/4 " − " 2)+9/8 sin^(−1)⁡〖((2√2)/3)−9/8 sin^(−1)⁡〖(0)〗 〗 = √2/2×√(1/4)+9/8 sin^(−1)⁡〖((2√2)/3)−9/8×0〗 = √𝟐/𝟒+ 𝟗/𝟖 sin−1((𝟐√𝟐)/𝟑) Area OCD Area OCD = ∫_0^(√2)▒𝑦 dx y → Equation of parabola x2 = 4y y = 𝒙^𝟐/𝟒 So, Area OCD = ∫_0^(√2)▒𝑦 dx = ∫_𝟎^(√𝟐)▒𝒙^𝟐/𝟒 dx = 1/4 ∫_0^(√2)▒𝑥^2 dx = 𝟏/𝟒 [𝒙^𝟑/𝟑]_𝟎^√𝟐 = 1/4 [(√2)^3/3−0^3/3] = 1/4 [(√2×√2×√2)/3−0] = 𝟏/𝟒 [(𝟐√𝟐)/𝟑] = √𝟐/𝟔 Now, Area BOC = Area BCDO − Area OCD = √𝟐/𝟒 + 𝟗/𝟖 〖𝒔𝒊𝒏〗^(−𝟏)⁡((𝟐√𝟐)/𝟑) – √𝟐/𝟔 = √2/4 − √2/6+9/8 sin^(−1)⁡((2√2)/3) = √𝟐/𝟏𝟐 +𝟗/𝟖 〖𝒔𝒊𝒏〗^(−𝟏)⁡((𝟐√𝟐)/𝟑) Required Area = Area ABCO = 2 × Area BOC = 2 × [√𝟐/𝟏𝟐+𝟗/𝟖 〖𝒔𝒊𝒏〗^(−𝟏)⁡((𝟐√𝟐)/𝟑) ] = √𝟐/𝟔+𝟗/𝟒 〖𝒔𝒊𝒏〗^(−𝟏)⁡((𝟐√𝟐)/𝟑)