



Chapter 4 Class 12 Determinants
Question 9 Important Deleted for CBSE Board 2024 Exams
Question 10 Important Deleted for CBSE Board 2024 Exams You are here
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 7 Important Deleted for CBSE Board 2024 Exams
Question 8 (i) Important Deleted for CBSE Board 2024 Exams
Question 11 (i) Deleted for CBSE Board 2024 Exams
Question 12 Important Deleted for CBSE Board 2024 Exams
Question 13 Important Deleted for CBSE Board 2024 Exams
Question 14 Important Deleted for CBSE Board 2024 Exams
Question 15 (MCQ) Important Deleted for CBSE Board 2024 Exams
Example 7 Important
Ex 4.2, 2 Important
Ex 4.2, 3 (i) Important
Example 13 Important
Example 15 Important
Ex 4.4, 10 Important
Ex 4.4, 15 Important
Ex 4.4, 18 (MCQ) Important
Ex 4.5, 13 Important
Ex 4.5, 15 Important
Ex 4.5, 16 Important
Question 14 Important Deleted for CBSE Board 2024 Exams
Question 15 Important Deleted for CBSE Board 2024 Exams
Question 1 Important Deleted for CBSE Board 2024 Exams
Question 5 Important Deleted for CBSE Board 2024 Exams
Question 9 Important Deleted for CBSE Board 2024 Exams
Misc 7 Important
Misc 9 (MCQ) Important
Chapter 4 Class 12 Determinants
Last updated at April 16, 2024 by Teachoo





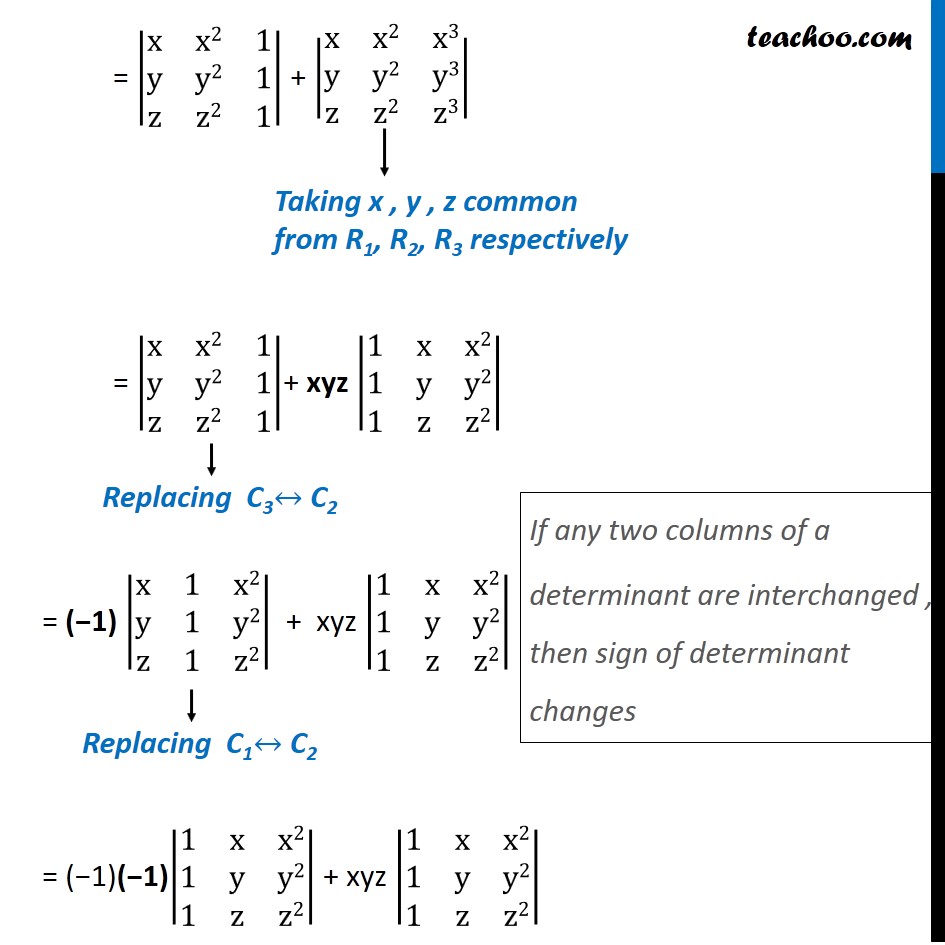
Question 10 If x, y, z are different and Δ = |■8(x&x2&1+x3@y&y2&1+y3@z&z2&1+z3)| = 0 , then show that 1 + xyz = 0 Solving ∆ = |■8(x&x2&1+x3@y&y2&1+y3@z&z2&1+z3)| Here, expanding elements of C3 into two determinants = |■8(x&x2&1@y&y2&1@z&z2&1)| + |■8(x&x2&x3@y&y2&y3@z&z2&z3)| = |■8(x&x2&1@y&y2&1@z&z2&1)| + |■8(x&x2&x3@y&y2&y3@z&z2&z3)| = |■8(x&x2&1@y&y2&1@z&z2&1)|+ xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = (−1) |■8(x&1&x2@y&1&y2@z&1&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = (−1)(−1)|■8(1&x&x2@1&y&y2@1&z&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| Taking x , y , z common from R1, R2, R3 respectively Replacing C3↔ C2 Replacing C1↔ C2 If any two columns of a determinant are interchanged , then sign of determinant changes = |■8(1&x&x2@1&y&y2@1&z&z2)| + xyz |■8(1&x&x2@1&y&y2@1&z&z2)| = |■8(1&x&x2@1&y&y2@1&z&z2)| (1 + xyz) Using R2 → R2 – R1 and R3 → R3 – R1 = |■8(1&x&x2@𝟏 −𝟏&y−x&y2 −x2@𝟏−𝟏&z−x&z2 −x2)| (1+ xyz) = |■8(1&x&x2@𝟎&(y−x)&(y −x)(y+x)@𝟎&(z−x)&(z −x)(z+x))| (1+ xyz) Taking common factor (y – x) from R2 & (z – x) from R3 = (1 + xyz) (y – x) (z – x) |■8(1&x&x2@0&1&y+x@0&1&z+x)| Expanding determinant = (1 + xyz) (y – x) (z – x) (z – y) (1|■8(1&𝑦+𝑥@1&𝑧+𝑥)|" – 0 " |■8(𝑥&𝑥2@1&𝑧+𝑥)|" + 0" |■8(𝑥&𝑥2@1&𝑦+𝑥)|) = (1 + xyz) (y – x) (z – x) (1 (y + x) – (y + x) + 0 + 0) = (1 + xyz) (y – x) (z – x) (z + y – y – x) = (1 + xyz) (y – x) (z – x) (z – y) ∴ ∆ = (1 + xyz) (y – x) (z – x) (z – y) Since ∆ = 0 given (1 + xyz) (y – x) (z – x) (z – y) = 0 Since it is given that x, y, z all are different, i.e., y – x ≠ 0, z – x ≠ 0, z – y ≠ 0, So, only Possibility is (1 + xyz) = 0 Hence Proved