

Ex 10.3
Ex 10.3, 2 Important
Ex 10.3, 3
Ex 10.3, 4
Ex 10.3, 5 Important
Ex 10.3, 6
Ex 10.3, 7 Important
Ex 10.3, 8
Ex 10.3, 9
Ex 10.3, 10
Ex 10.3, 11 Important
Ex 10.3, 12 Important
Ex 10.3, 13
Ex 10.3, 14 Important
Ex 10.3, 15
Ex 10.3, 16 Important
Ex 10.3, 17
Ex 10.3, 18 Important
Ex 10.3, 19 Important
Ex 10.3, 20
Ex 10.3
Last updated at April 16, 2024 by Teachoo



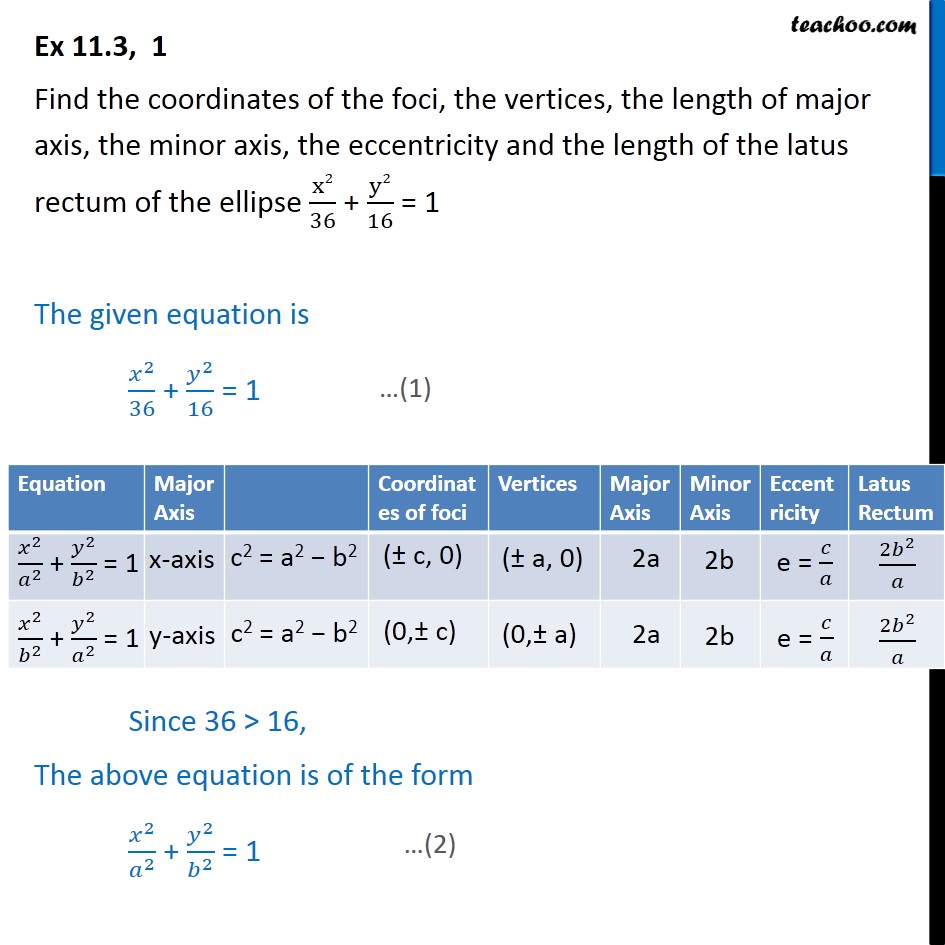
Ex 10.3, 1 Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse x236 + y216 = 1 The given equation is 𝑥236 + 𝑦216 = 1 Since 36 > 16, The above equation is of the form 𝑥2𝑎2 + 𝑦2𝑏2 = 1 Comparing (1) and (2) We know that c2 = a2 − b2 c2 = 62 – 42 c2 = 36 − 16 c2 = 20 c = 20 c = 2 × 2 × 5 c = 2𝟓 Coordinates of foci = ( ± c, 0) = (± 25, 0) So, coordinates of foci are (25, 0) & (−25, 0) Vertices = (± a, 0) = (± 6, 0) Thus vertices are (6, 0) and (–6, 0) Length of major axis = 2a = 2 × 6 = 12 Length of minor axis = 2b = 2 × 4 = 8 Eccentricity is e = 𝑐𝑎 = 256 Latus Rectum = 2𝑏2𝑎 = 2 × 426 = 163