



Miscellaneous
Misc 1 (ii) Important
Misc 2 Important
Misc 3 Important
Misc 4 (MCQ)
Misc 5 (MCQ) Important
Question 1 Deleted for CBSE Board 2024 Exams
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Important Deleted for CBSE Board 2024 Exams
Question 4 Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams
Question 7 Deleted for CBSE Board 2024 Exams
Question 8 Important Deleted for CBSE Board 2024 Exams You are here
Question 9 Important Deleted for CBSE Board 2024 Exams
Question 10 Deleted for CBSE Board 2024 Exams
Question 11 Important Deleted for CBSE Board 2024 Exams
Question 12 Deleted for CBSE Board 2024 Exams
Question 13 (MCQ) Deleted for CBSE Board 2024 Exams
Question 14 (MCQ) Important Deleted for CBSE Board 2024 Exams
Miscellaneous
Last updated at April 16, 2024 by Teachoo





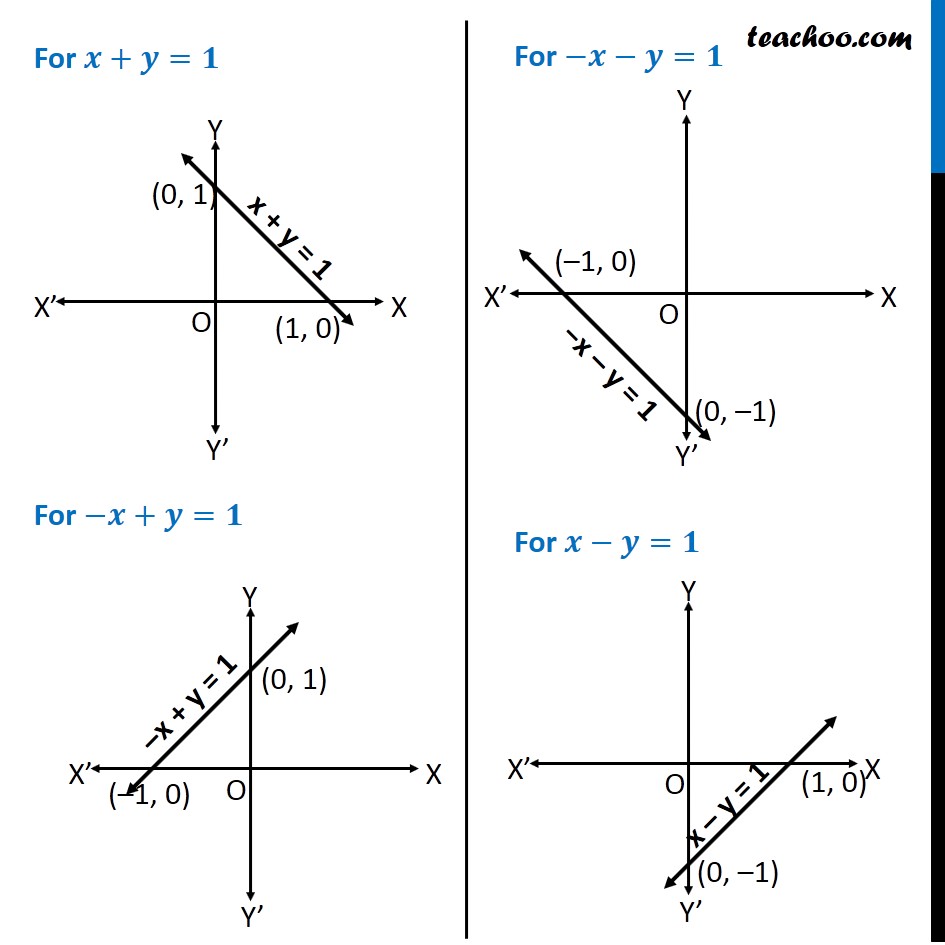
Question 8 Using the method of integration find the area bounded by the curve |𝑥|+|𝑦|=1 [Hint: The required region is bounded by lines 𝑥+𝑦= 1, 𝑥 –𝑦=1, –𝑥+𝑦 =1 and −𝑥 −𝑦=1 ] We know that "│" 𝑥"│"={█(𝑥, 𝑥≥0@&−𝑥, 𝑥<0)┤ & "│" 𝑦"│"={█(𝑦, 𝑦≥0@&−𝑦, 𝑦<0)┤ So, we can write │𝑥"│+│" 𝑦"│"=1 as {█(█(█( 𝑥+𝑦=1 𝑓𝑜𝑟 𝑥>0 , 𝑦>0@−𝑥+𝑦=1 𝑓𝑜𝑟 𝑥<0 𝑦>0)@█( 𝑥−𝑦 =1 𝑓𝑜𝑟 𝑥>0 , 𝑦<0@−𝑥−𝑦=1 𝑓𝑜𝑟 𝑥<0 𝑦<0)))┤ For 𝒙+𝒚=𝟏 For −𝒙+𝒚=𝟏 For −𝒙−𝒚=𝟏 For 𝒙−𝒚=𝟏 Joining them, we get our diagram Since the Curve symmetrical about 𝑥 & 𝑦−𝑎𝑥𝑖𝑠 Required Area = 4 × Area AOB Area AOB Area AOB = ∫_0^1▒〖𝑦 𝑑𝑥〗 where 𝑥+𝑦=1 𝑦=1−𝑥 Therefore, Area AOB = ∫_0^1▒〖(1−𝑥) 𝑑𝑥〗 = [𝑥−𝑥^2/2]_0^1 =1−〖 1〗^2/2−(0−0^2/2)^2 =1−1/2 =1/2 Hence, Required Area = 4 × Area AOB = 4 × 1/2 = 2 square units